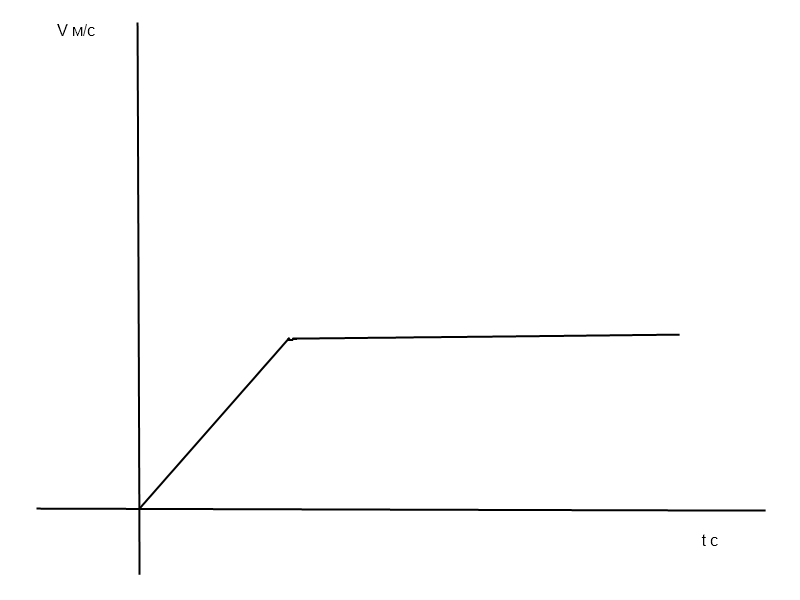
Как движется автомобиль график проекции скорости движения которого изображен на рис 21 рис
Сначала равноускорено, потом равномерно.
На рисунке показано, как меняется с течением времени проекция вектора скорости тела?
На рисунке показано, как меняется с течением времени проекция вектора скорости тела.
Пользуясь графиком, определите проекцию \ ах \ и модуль |а| вектора ускорения, с которым движется это тело.
Автомобиль движется по прямой улице?
Автомобиль движется по прямой улице.
лена зависимость проекции скорости автомобиля от времени.
Определите проекцию максимального ускорения автомобиля.
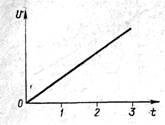
Вопрос : на рисунке изображён график скорости равномерного движения?
Вопрос : на рисунке изображён график скорости равномерного движения.
Определите путь пройденный телом за 3 с.
Автомобиль движется по прямой улице?
Автомобиль движется по прямой улице.
На графике представлена проекция зависимости автомобиля от времени.
Определите проекцию максимального ускорения автомобиля.
Физика 10 скорость На рисунке приведен график зависимости проекции скорости некоторого тела от времени?
Физика 10 скорость На рисунке приведен график зависимости проекции скорости некоторого тела от времени.
Определите проекцию перемещения этого тела за 5с после начала движения.
СРОЧНО?
На рисунке представлен график зависимости проекции скорости движения тела от времени.
Добавить правильную зависимость проекции ускорения от времени, соответствующий этому движению.
На рисунке изображены графики зависимости проекции скорости тел от времени?
На рисунке изображены графики зависимости проекции скорости тел от времени.
Опишите движение тел.
Тело движется вдоль оси ОХ?
Тело движется вдоль оси ОХ.
На рисунке представлен график зависимости проекции скорости движения этого тела от времени.
Опишите движение тела (укажите скорость его движения в момент начала наблюдения, укажите направление и характер движения тела).
Определите ускорение движения тела.
Запишите уравнение зависимости проекции скорости и координаты тела от времени.
Тело движется вдоль оси ОХ?
Тело движется вдоль оси ОХ.
На рисунке представлен график зависимости проекции скорости движения этого тела от времени.
Опишите движение тела (укажите скорость его движения в момент начала наблюдения, укажите направление и характер движения тела).
Определите ускорение движения тела.
Запишите уравнение зависимости проекции скорости и координаты тела от времени.
ПОМОГИТЕ?
На рисунке изображен график зависимости проекции скорости гоночного автомобиля от времени.
Выполните задания, опираясь на данные рисунка.
А) Определите начальную скорость автомобиля и вычислите ускорение его движения.
Б) Опишите движение автомобиля.
В) Составьте уравнения зависимостей проекции скорости и координаты от времени, считая, что начальная координата равна 200 м.
V = 30м/мин = 0,5 м/сек,
t = 2S/V = 2*0,18/0,5 = 0,72 сек
a = V/t = 0,5/0,72 = 25/36 = 0,7 м/с²
Проверка:
S = at²/2 = 0,7*0,72²/2 = 0,18 м
V = at = 0,7*0,72 = 0,5 м/с
1)
Находим период колебаний волны:
T = λ / V = 6/25 = 0,24 с
2)
Находим циклическую частоту:
ω = 2π / T = 2π / 0,24 ≈ 8,3·π с⁻1
3)
Перемещение частицы среды за период равно:
S = 0
5)
Максимальную скорость найдем из уравнения колебаний, взяв первую производную:
x(t) = Xmax*sin (ω*t+φ₀)
v(t) = x’ (t) = ω*Xmax*cos(ω*t+φ₀)
Vmax = ω*Xmax = 8,3·π·0,5 ≈ 8,3·3,14*0,5 ≈ 13 м/с
Запишем уравнение волны:
По условию:
Xmax/2 = Xmax*sin (φ₀)
1/2 = sin (φ₀)
φ₀ = π/6
Имеем:
x(t) = Xmax*sin (ω*t+φ₀) = 0,5*sin (8,3π*t + π/6)
1. Вещества в каком состоянии могут легко менять свою форму и объем?
В. В газообразном;
2. Автомобиль за 5 мин прошел путь 6км 600м. Какова скорость автомобиля?
Г. 22 м/с.
v = s/t = 6600 м/5*60 сек = 22 м/с
3. Каким явлением можно объяснить фразу: «Вода в реке становилась мутной»?
Не очень корректный вопрос. Если понимать диффузию, как смешивание, то диффузия.
А. Диффузией;
4. Мотоцикл «ИжП5» имеет массу 195кг. Каким станет его вес, если на него сядет человек массой 80кг?
Вес это сила, с которой давит на опору или растягивает нить подвеса тело. Тогда Р= (195+80)кг*10 м/c^2 = 2750 Н
В. 2750 Н;
5. Два человека несут бревно весом 800Н. С какой силой бревно давит на каждого их них?
На каждого из них по 800/2 = 400Н. Каждый из них давит на бревно по направлению вверх с силой 400 Н (реакция опоры) и сумма этих сил должны быть равна силе тяжести.
Б. 400Н;
6. При действии на опору силой 20 Н давление на нее оказывается в 200 Па. Во сколько раз изменится давление, если площадь опоры уменьшить в два раза?
Давление обратно пропорционально площади опоры. Уменьшение площади в 2 раза вызовет увеличение давления в 2 раза.
А. Увеличится в 2 раза;
7. При поднятии груза весом 140 Н с помощью подвижного блока на веревку действовали с силой 76 Н. Каков вес блока?
Г. 6 Н
8. Определите вес воды в бассейне размерами 25м х 4м х 2м. Плотность воды 1000 кг/м3.
Объем воды V = 25*4*2 = 200 м^3, тогда вес воды равен
Конспект урока: «Решение задач по теме: « Кинематика»»
Физика 9 класс урок №11 12.10.17
Решение задач по теме: « Кинематика»
Обучающая цель: формирование умений и навыков решения физических задач графическим способом, исследовательской работы и умений обосновывать свой вариант решения.
Развивающая цель: развитие у школьников теоретического, творческого мышления, формирование операционного мышления, направленного на выбор оптимальных решений
Мотивационная цель: пробуждение интереса к изучению физики
Воспитательная – развитие познавательного интереса и коллективизма у школьников.
Учебная – обучение и закрепление основных навыков решения кинематических задач графическим способом
Повторение. Проверка домашнего задания
2. Актуализация опорных знаний :
— Начальная и конечная скорости движения тела (тело движется в одном направлении) соответственно равны 2 м/с и 4 м/с. Как движется это тело?
— Поезд отходит от станции. Как направлено его ускорение?
— Поезд начинает тормозить. Как направлены его ускорение и скорость?
Следует анализ формул.
Делается вывод: равномерное движение является частным случаем равноускоренного движения.
3. Как движется автомобиль, график проекции скорости движения которого изображен на рис. 21?
4. Автомобиль, остановившийся перед светофором, набирает затем скорость 54 км/ч на пути 50 м. С каким ускорением он должен двигаться? Сколько времени будет длиться разгон? (Ответ: 2,25 м/с 2 ; 6,7 с.)
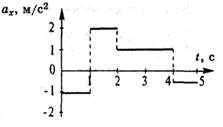
5. По данному на рис. 22 графику проекции ускорения построить график проекции скорости, если начальная скорость v 0 = 0.
4. Домашнее задание: подготовка к к/р, задачи.
1. Велосипедист движется в течение некоторого времени с постоянной скоростью 2 м/с. Затем его движение становится равноускоренным, и он проходит за 20 с путь в 250 м. Какой будет конечная скорость велосипедиста? (Ответ: 23 м/с.)
2. Тело, двигаясь с ускорением 10 м/с 2 из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. Какой скорости достигнет тело в конце пути? Сколько времени двигалось тело? Какой путь оно прошло? (Ответ: S = 40 м, t = 2,8 с, v 2 = 28 м/с.)
3. На рис. 25 представлен график зависимости проекции скорости от времени. В какой из четырех интервалов времени тело прошло максимальный путь?
5. Итоги. Выставление оценок. Рефлексия: я могу… я умею… я знаю…
Развитие навыков самостоятельной работы. Отработка методов решения задач.
I. Повторение. Проверка домашнего задания
Вопросы и задачи на повторение:
— Начальная и конечная скорости движения тела (тело движется в одном направлении) соответственно равны 2 м/с и 4 м/с. Как движется это тело?
— Поезд отходит от станции. Как направлено его ускорение?
— Поезд начинает тормозить. Как направлены его ускорение и скорость?
Следует анализ формул.
Делается вывод: равномерное движение является частным случаем равноускоренного движения.
II. Самостоятельная работа
3. Как движется автомобиль, график проекции скорости движения которого изображен на рис. 21?
4. Автомобиль, остановившийся перед светофором, набирает затем скорость 54 км/ч на пути 50 м. С каким ускорением он должен двигаться? Сколько времени будет длиться разгон? (Ответ: 2,25 м/с 2 ; 6,7 с.)
5. По данному на рис. 22 графику проекции ускорения построить график проекции скорости, если начальная скорость v0 = 0.
3. Как движется велосипедист, график проекции скорости движения которого изображен на рис. 23?
4. При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определите путь тела за седьмую секунду. (Ответ: 1,3 м.)
5. По данному на рис. 24 графику проекции ускорения построить график проекции скорости, если начальная скорость v0 = 0.
1. Велосипедист движется в течение некоторого времени с постоянной скоростью 2 м/с. Затем его движение становится равноускоренным, и он проходит за 20 с путь в 250 м. Какой будет конечная скорость велосипедиста? (Ответ: 23 м/с.)
2. Тело, двигаясь с ускорением 10 м/с 2 из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. Какой скорости достигнет тело в конце пути? Сколько времени двигалось тело? Какой путь оно прошло? (Ответ: S = 40 м, t = 2,8 с, v2 = 28 м/с.)
3. На рис. 25 представлен график зависимости проекции скорости от времени. В какой из четырех интервалов времени тело прошло максимальный путь?
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ
Начальный уровень:
А1. Расскажите о движении тела, график проекции скорости которого изображен на рисунке.
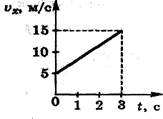


А2. Расскажите о движении тела, график проекции скорости которого изображен на рисунке.
А3. Расскажите о движении тела, график проекции ускорения которого изображен на рисунке.
А4. Как двигался автомобиль, график проекции скорости движения которого изображен на рисунке?
А5. Расскажите о движении тела, график проекции ускорения которого изображен на рисунке.



А6. Как двигался велосипедист, график проекции скорости движения которого изображен на рисунке?
Средний уровень:
Б1. (54.P) Зависимость скорости от времени при разгоне автомобиля задана формулой vx = 0,8 t. Построить график скорости и найти скорость в конце пятой секунды.
Б2. Зависимость скорости от времени движущегося тела задана формулой vx = 1 + 2t. Опишите это движение (укажите значения характеризующих его величин), постройте график vx (t).
Б3. (55.P) Скорость поезда за 20 с уменьшилась c 72 до 54 км/ч. Написать формулу зависимости скорости от времени vx (t) и построить график этой зависимости.
Б4. (57.P) По заданным на рис.Б4 графикам написать уравнения vx = vx (t).
Б5. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени vx (t), x(t).

Б8. Зависимость скорости от времени движущегося тела задана формулой vx = 4 + t. Опишите это движение (укажите значения характеризующих его величин), постройте график vx (t).
Б9. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени vx (t), x (t).
Б10. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени (vx(t), x(t)).
Б12. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени vx (t), x(t).
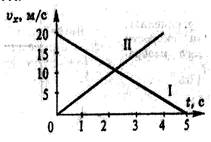

Рис.Б10 Рис.Б12 Рис.Б13
Б13. (59.P) По графикам зависимости ах (t), приведенным на рис.Б13, а и б, построить графики зависимости vx (t). считая, что в начальный момент времени (t = 0) скорость движения материальной точки равна нулю.
Достаточный уровень:

В1. По данному графику проекции скорости построить графики для координаты и проекции ускорения.
В2. По данному графику проекции ускорения построить графики для координаты и проекции скорости.
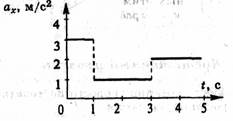
В3. По данному графику проекции скорости построить графики для координаты и проекции ускорения.
В4. По данному графику проекции ускорения построить графики для координаты и проекции скорости.
В5. По данному графику проекции скорости построить графики для координаты и проекции ускорения.
В6. По данному графику проекции ускорения построить графики для координаты и проекции скорости.
В7. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

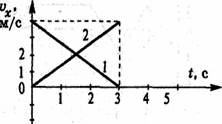
В8. Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно сказать о путях, пройденных этими телами за время 3c от начала отсчета времени? Постройте графики пути для обоих тел.

В10. (38.Т) На рис.В10 даны графики ускорений четырех движущихся тел. Как движутся эти тела?
Высокий уровень:
Г1. Как двигался мотоциклист, график проекции скорости движения которого изображен на рисунке? Начертите график пути, соответствующий данному графику.
Г2. По данному графику проекции скорости построить графики для координаты и проекции ускорения.
Г3. По данному графику проекции ускорения построить, графики для координаты и проекции скорости.
Г4. По данному графику проекции скорости построить графики для координаты и проекции ускорения.
Г5. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

Г6. По данному графику проекции ускорения построить графики для координаты и проекции скорости.
Олимпиадные задачи:
Д1. Как двигалось тело, график ускорения которого дан на рисунке. Начертите (качественно) графики скорости и пути, соответствующие данному графику ускорения.
Д2. На рисунке даны графики проекции скоростей для двух точек, движущихся по одной прямой от одного и того же начального положения. Известны моменты времени t1 и t2. В какой момент времени t3 точки встретятся? Построить графики движения x(t).
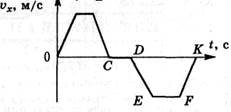
Д3. (51Т) На рисунке 17 дан график скорости тела, движущегося прямолинейно. Постройте график его перемещения и ускорения, если треугольники ОАВ, BCD, DEK равны.