Как работать с машиной тьюринга
Машина Тьюринга: описание и примеры машин Тьюринга
Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.
Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В=<0.1>. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
Программа для устройства
Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 0 | 1 | 2 | 3 | . | 7 | 8 | 9 | |
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
Тема 9 Элементы теории алгоритмов
9.1 Машины Тьюринга
9.2 Рекуррентные функции
9.3 Тезисы Тьюринга и Чёрча
Понятие алгоритма стихийно формировалось с древнейших времен. Современный человек понимает под алгоритмом четкую систему инструкций о выполнении в определенном порядке некоторых действий для решения всех задач какого-то данного класса.
Многочисленные и разнообразные алгоритмы окружают нас буквально во всех сферах жизни и деятельности.
Большое количество алгоритмов встречаются при изучении математики буквально с первых классов школы. Это, прежде всего, алгоритмы выполнения четырех арифметических действий над различными числами – натуральными, целыми, дробными, комплексными. Примерами известных алгоритмов являются алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел, вычисление определителей различных порядков, вычисление рангов матриц с рациональными элементами, приближенное вычисление корней уравнений и т. д.
В начале ХХ века у математиков начали возникать подозрения в том, что некоторые массовые задачи, по-видимому, не имеют алгоритмического решения. Для точного доказательства несуществования алгоритма необходимо иметь его точное математическое определение. Первые работы по уточнению понятия алгоритма и его изучению были выполнены в 1936–1937 гг. А. Тьюрингом, Э. Постом, К. Геделем, А. А. Марковым, А. Черчем. Было выработано несколько определений понятия алгоритма, но впоследствии выяснилось, что все они равносильны между собой, то есть определяют одно и то же понятие.
9.1 Машины Тьюринга. Машины Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Она есть такой же математический объект, как функция, производная, интеграл и т. д. А так же, как и другие математические понятия, понятие машина Тьюринга отражает объективную реальность, моделирует некие реальные процессы.
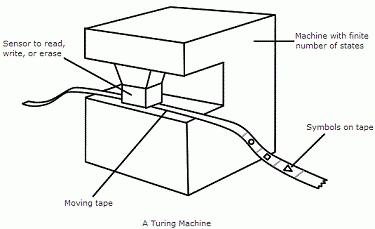
Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки.
Лента разбита на ячейки. Во всякой ячейки в каждый момент времени находится в точности один символ из внешнего алфавита А=<а0,а1,…аn-1 >, n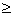
Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита.
Работа машины Тьюринга определяется программой. Программа состоит из команд. Каждая команда представляет собой выражение одного из следующего вида:
Команда 1 заключается в том, что содержимое aj обозреваемой на ленте ячейки стирается, а на его места дописывается символ ae (который может совпадать с aj ), машина переходит в новое состояние qk (оно может совпадать с предыдущим состоянием qi ).
Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.
Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку.
Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии.
Машинным словом или конфигурацией называется слово вида
Где аij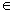
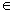

Например, конфигурация 13q10212 на ленте выглядит следующим образом:
Машина Тьюринга — одно из самых важных открытий XX века
Тема: Наука
В 30-е годы XX века английский математик Алан Тьюринг придумал такое странное устройство, которое теперь называют машиной Тьюринга.
Идея его была в том, чтобы придумать устройство, абстрактную машину, которая может делать все, что вообще могут делать машины. Он был не единственным в этот момент, другие люди тоже в других терминах определяли похожие вещи, но в гораздо более абстрактных терминах, по крайней мере, в их работах конкретного механизма работы машины не было.
Факт №1
Оказалось же, что это одно из самых важных открытий XX века. То, что сейчас в разных устройствах — скажем, в телевизоре и в стиральной машине, — может использоваться одна и та же микросхема процессора, — это воплощение одной из идей Тьюринга.
И то, что одна и та же программа может использоваться в самых разных компьютерах, работать с самой разной аппаратурой и выглядеть одинаково, это тоже его идея. Тогда это называлось идеей хранимой программы (программа хранится в памяти и определяет поведение машины), и ещё была идея универсальной машины, — есть машина, которая может делать все, что может делать любая другая машина.
Если бы не Тьюринг, наверно, это придумал бы кто-то другой, он не был единственным, кто над этим работал, но так или иначе такое абстрактное теоретическое устройство оказалось одним из самых важных изобретений в XX веке.
Факт №2
Интересно, что потом Тьюринг, когда настали трудные времена, не только занимался теорией, но и практически участвовал в разных важных проектах.
Он с коллегами расшифровал коды немецкой армии — это известная история. Там использовались шифровальные машины «Энигма», которые пытались расшифровать сначала польские криптографы, а потом английские — при активном участии Тьюринга, и им это удалось.
А после войны Тьюринг уже строил реальную электронную вычислительную машину. Хотя прямой связи с его теоретическими работами не было, но явно это было продолжением той же самой деятельности. Так что хорошая теория — вещь очень практичная, и не надо бояться того, что теоретические работы окажутся бесполезными.
Факт №3
Сейчас это большая наука, которая называется теория сложности вычислений, в ней много всего интересного открыли, но есть самая главная проблема, которая называется проблема перебора, и которая до сих пор не решена.
Ее можно объяснить на таком примере: выпускалась игрушка Eternity — это такая коробочка, в которую уложены плитки, раскрашенные в разные цвета, но они раскрашены так, что видно, какие плитки можно прикладывать друг к другу (там рисунок на краях). Продаются они рассыпанными, и фирма, которая их изготовила, утверждает, что все это можно собрать в одну картинку внутри этой квадратной коробки (там 256 плиток) — то есть что изначально это была одна картинка, разрезанная на плитки.
По современным представлениям, машины такие задачи за обозримое время решать не могут, никакого способа, кроме как перебирать все варианты (а их очень много) сейчас не известно. Но, с другой стороны, никто этого не может и доказать. Это и называется проблемой перебора — доказать, что такой полный перебор каких-то объектов нельзя заменить никаким более коротким вычислением.
Факт №4
В 2000-м году был публично объявлен «список проблем следующего тысячелетия», за которые Институт Клея обещает миллион долларов.
Так вот, первая проблема в этом списке — это проблема перебора, и она там заслуженно. Интересно в теории сложности вычислений то, что не только наличие какого-то алгоритма полезно практически, но, как ни странно, часто бывает полезно отсутствие алгоритма.
Например, есть такой известный вопрос о разложении чисел на множители. Если число небольшое, то легко проверить, что оно простое — можно проверить все меньшие числа, и понять, что там нет делителей. Если число большое, то так просто уже нельзя проверить — но существуют разные алгоритмы, которые позволяют это делать. (Они основаны на малой теореме Ферма и её усовершенствованиях, но это отдельная тема.)
Так или иначе, алгоритмы проверки простоты существуют. А теперь другая задача: возьмём два больших простых числа и их перемножим, сообщим, что у нас получилось, и спросим, какие это были числа. Это задача разложения на множители, и никто не знает, как это быстро сделать. И то, что этого никто не знает, очень хорошо, потому что благодаря этому существует вся вычислительная криптография, это одно из основных её предположений.
Когда кто-нибудь снимает деньги в банке, или в Интернете заходит на сайт с помощью SSL — используются системы криптографии, основанные на том, что быстро разлагать на множители числа нельзя. Если кто-нибудь в какой-то момент обнаружит, что разлагать можно, то, думаю, после этого будет экономический кризис, потому что вся банковская система рухнет, пока люди не заменят это чем-то другим (вообще без использования компьютеров или с какими-то новыми алгоритмами).
Так что отсутствие алгоритма может быть полезнее, чем его наличие. К сожалению, никто не может доказать, что алгоритма нет, хотя все подозревают, что это так — не решена ни общая проблема перебора, ни этот частный ее случай (разложение чисел на множители), особенно важный, и про него тоже все думают, но никто ничего не придумал.
Факт №5
Что такое случайность? Это дело тонкое, вообще, существует ли случайность? Когда в каком-нибудь казино играют в рулетку — может ли наука предсказать, что там выпадет, и как нужно играть, чтобы выиграть, или это в принципе невозможно?
Федор Михайлович Достоевский твердо верил, что если быть хладнокровным и не волноваться во время игры, то можно выиграть, — он говорил, что, к сожалению, ему не удаётся быть хладнокровным, и поэтому он всё время проигрывал.
С другой стороны, теория вероятностей основана на том, что такой системы не существует, что последовательность бросания монеты в какой-нибудь игре, или последовательность выпадения красного и черного в рулетке, случайны и непредсказуемы. Но возникает вопрос, что такое случайность? Как определить, что это значит? Можем ли мы отделить случайное от неслучайного?
Сейчас вы видите две последовательности:
Вам сказано, что одна из них получена бросанием монеты, а другая как-то иначе. Сможете ли вы определить, какая из них получена каким образом?
Я думаю, что сможете, и что более-менее всякий человек, который посмотрит на эту картинку, скажет, что первая последовательность получена не бросанием монеты, а просто чередованием 0 и 1, а вторая вполне может быть получена бросанием монеты.
Но спрашивается, в чём разница? Почему вы смотрите на эту картинку и уверены, что первая последовательность не может быть получена бросанием монеты? Почему монета не может выпасть сначала орлом, потом решкой, потом снова орлом… как это объяснить? Можно сказать так: вероятность того, что это случайно произойдет, очень мала, потому что такая последовательность всего одна, а всего последовательностей очень много. Но ведь то же самое можно сказать и про вторую последовательность, появление конкретно этой последовательности имеет ту же самую малую вероятность, что и для первой. Поэтому вопрос — в чём тут разница, чем первая последовательность «лучше» второй (менее случайна, чем вторая)?
Факт №6
Или другой парадоксальный пример. Представьте себе, как в XIX веке (это написано у Лотмана в его «Беседах о русской культуре») играли в карты. В отличие от нынешней ситуации, когда карты тасуют, тогда карты продавались уже перетасованными заранее.
Поэтому дворяне, которые играли в серьезные игры, каждый раз брали новую колоду и играли с ней. После этого она выбрасывалась и поступала, как пишет Лотман, в распоряжение слуг, которые играли в своего «подкидного дурака».
Так вот, представим себе, что есть фабрика, которая выпускает такие перетасованные колоды и есть машина, которая печатает карты, а есть, которая их тасует — эта машина их как-то внутри себя тасует, потом выкладывает, запаковывает, и они поступают в продажу. Теперь представим себе, что на этой фабрике есть, как говорили в советское время, «отдел технического контроля», который должен проверять, хорошо ли они перетасованы.
Время от времени он из пачки сделанных колод достаёт одну колоду, распаковывает и смотрит, хорошо ли она перетасована. С одной стороны, он должен что-то контролировать, то есть если он никогда никакие колоды не будет браковать как негодные, то зачем он вообще нужен? А с другой стороны, непонятно, что он может контролировать, потому что вся идея того, что карты хорошо перетасованы, состоит в том, что все варианты, все возможные последовательности карт в колоде, имеют совершенно одинаковую вероятность.
Соответственно, ни одна из них, с точки зрения тасовальной машины, не лучше другой. Почему же мы некоторые колоды (некоторые последовательности карт) бракуем, а некоторые оставляем? Это как-то загадочно.
Если, скажем, все карты идут в порядке возрастания их значения, или сначала идут все красные карты, а потом черные — такие комбинации, вроде бы, надо браковать. Но, с другой стороны, непонятно, чем они хуже других. Одной из попыток ответить на этот вопрос (60-е годы XX века) было понятие сложности, то, что сейчас называется колмогоровская сложность или алгоритмическая сложность.
Факт №7
Идея эта совсем простая — что первая из последовательностей
потому выглядит неслучайной, что она проста. «Проста» значит, что существует очень короткий способ объяснить, как она устроена — сказать, что там нули и единицы чередуются. В нашем примере такая разница, может, не сильно заметна — но если там будет тысяча чередующихся нулей и единиц, то ясно, что короче это объяснить словами, чем выписывать всю последовательность.
А для настоящей случайной монеты (как считается в рамках этого объяснения случайности) — никакого способа описать последовательность более коротким способом, чем показав просто все нули и единицы, как они есть, не существует.
Можно сказать, что, если мы начнем «сжимать» последовательности каким-то архиватором, то вторая последовательность не сожмётся, а первая сожмется.
В этом и состоит основная идея Колмогорова и его коллег, которые придумали, что сложность последовательности — это длина кратчайшей программы, которая такую последовательность может напечатать, а случайные последовательности отличаются от неслучайных тем, что нельзя их напечатать никакой программой, которая короче, чем сама последовательность.
Теперь целая наука на эту тему возникла, она называется алгоритмическая теория информации, алгоритмическая случайность, но, конечно, многие вопросы там еще не ясны. Не ясен вопрос о том, что можно сделать с ограничением на сложность вычислений.
Возможно, что последовательность на самом деле неслучайна и имеет какое-то короткое описание, но мы его просто не знаем и не можем найти — или проблема может быть не в том, что мы его не можем найти, а в том, что для того, чтобы восстановить последовательность по этому описанию, нужно очень много времени.
Вот это такая активно развивающаяся и, к сожалению, ещё не очень развитая область, и там, может быть, что-нибудь интересное в ближайшее время (или не в ближайшее время) откроют.
Если вы хотите получать больше статей, подобно этой, то кликните Recommend ниже.
Машина Тьюринга, как модель автоматных программ
Машина Тьюринга, как модель автоматных программ
1. Введение
Программирование нуждается в новых универсальных алгоритмических моделях, а аппаратные средства реализуют алгоритмы не только в другой форме, но и на базе другой алгоритмической модели — автоматной. Заимствование технологии из сферы разработки аппаратных средств ключевая идея автоматного программирования. Однако синтез цифровых устройств отличается от программирования. Но, заимствуя модель, с одной стороны, ее не желательно существенно изменять, а, с другой стороны, нельзя не учитывать уже существующую теорию и практику программирования.
Далее мы рассмотрим SWITCH-технологию проектирования автоматных программ, в которой с подобными процессами сталкиваешься сплошь и рядом. С одной стороны, она так изменила модель конечного автомата, что фактически вывела ее за рамки теории автоматов. А, с другой стороны, вводит в программирование понятия, которые с трудом воспринимаются программистами, а, порой, просто являются лишними, т.к. существуют более привычные аналоги из теории программ и практики программирования.
За основу обсуждения проблем автоматного программирования возьмем недавнюю лекцию Шалыто А.А. [1] и его «программные» статьи к определению парадигмы автоматного программирования [2, 3].
1. Автоматизированные объекты, схемы программ
В лекции достижением автоматного программирования объявлено введение в него понятия автоматизированных объектов управления, заимствованное из теории автоматического управления (ТАУ). Но, напомним, что в ТАУ рассматривают не столько объекты, а системы, среди которых выделяют следующие [4]:
Исходя из этого, правильнее было бы говорить о системах автоматического управления (САУ). Теперь посмотрим на типовую функциональную схему САУ, показанную рис. 1. Если ленту машины Тьюринга считать объектом управления, то исполнительными устройствами (ИсУ) будут элементы МТ, реализующие изменение содержимого ленты и передвигающие головку, а измерительными устройствами (ИзУ) — элементы, читающие информацию с ленты.

Рис.1. Функциональная схема САУ
Но зачем обращаться к ТАУ, если есть более близкая к программированию практика проектирования вычислительных систем, в которой операционные устройства (ОУ), к которым, безусловно, относится и МТ, рассматриваются в виде комбинации операционного (ОА) и управляющего (УА) автоматов. И это ближе к тому, к чему мы в конечном итоге стремимся — обоснованию мощности автоматного программирования. На рис. 2 представлен скрин текста из монографии Майорова С.А., Новикова Г.И. Структура электронных вычислительных машин [5], в которой вопросы проектирования ОУ рассмотрены весьма детально.

Рис.2. Концепция управляющего и операционного автоматов
Но, если сравнивать теорию проектирования ЭВМ и теорию программ, то между ними прослеживается явная структурная аналогия. В теории программирования модель любой программы на структурном уровне можно представить, как схему программы S = (M, A, C), где M – множество элементов памяти, A – множество операторов, C – управление [10]. Следуя этому подходу, любую программу машины Тьюринга также можно определить как схему программы, в которой множество M представлено ячейками ленты, множество операторов – действиями МТ, связанными 1) с анализом ячеек, 2) изменением символов в ячейках ленты и 3) перемещением головки.
Таким образом понятие схемы программы полностью аналогично рассмотренной концепции операционного и управляющего автоматов, где моделью УА является модель рассматриваемого далее структурного конечного автомата (СКА), а ОА «является структурой для выполнения действий над информацией». При этом ОА включает элементы хранения данных (выше – это память) и блоки для обработки информации, реализующих вычисление логических условий и реализацию тех или иных действий (выше – множество операторов).
Из сказанного можно понять, что лента лишь условно может считаться объектом управления для МТ. Хотя бы потому, что устройство управления машины Тьюринга не имеет к ней прямого доступа, т.к. все операции с ячейками реализуют опосредован-но блоки ОА. Кроме того, как представляется, не очень привычно или, если не сказать, странно считать целью управления программы, как системы управления, объект, представляющий собой память (ленту).
Таким образом, для формального определения машины Тьюринга, а в ее контексте места для модели конечного автомата, достаточно понятий теории программ. Теперь, в отличие от весьма расплывчатого определения автоматных программ, данного в рамках SWITCH-технологии, можно сказать, что автоматной программой считается программа, имеющая управление в форме модели конечного автомата.
Какая при этом будет сама программа – с простым или сложным поведением, какова ее «разновидность» – с логическим управлением, «с явным выделением состояний» и т.д. и т.п. не имеет абсолютно значения. Главное – вид управления. Остальные же элементы программы могут определяться в широких пределах – от простейших, как, например, у машины Тьюринга, до самых сложных – любых форм операторов, функций и структур данных языков программирования – ассемблера, языка высокого уровня и т.п.
Можно также вспомнить, что машину Тьюринга уже давно принято считать авто-матом [6] или уж, в крайнем случае, его простым расширением [7]. Но необходимо понимать, что это за автомат, что это за расширение, и эквивалентны ли они моделям классических конечных автоматов. Попробуем это как раз и уточнить.
2. Тьюрингово программирование в среде автоматного программирования
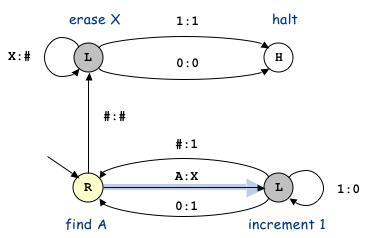
На рис. 3 показан автомат для МТ функции инкремента из монографии [8]. По форме это явно не программа для МТ, но уже и не классический конечный автомат. На рис. 4 приведен граф классического структурного конечного автомата (СКА) и его реализация в среде ВКПа (среда визуально-компонентного автоматного программирования на языке С++ в рамках библиотеки Qt и среды Qt Creator), реализующего тот же самый алгоритм блока управления (БУ) МТ.

Рис.3. Увеличение числа на единицу с помощью машины Тьюринга
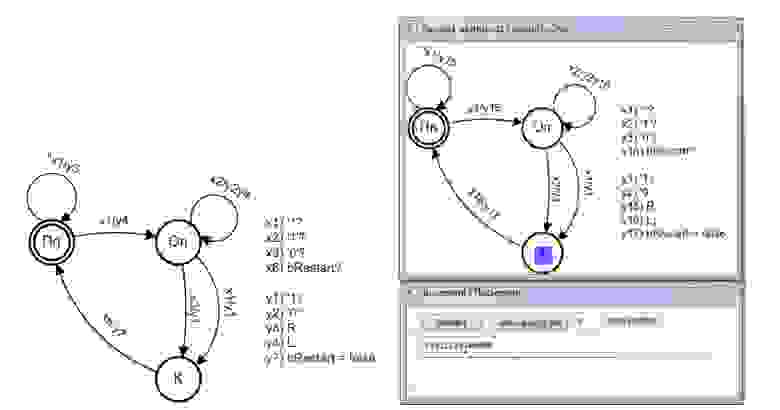
Рис.4 Модель программы инкремента для МТ в форме СКА
Можно видеть, что структурный автомат имеет четыре входных и пять выходных каналов. Каждый из этих каналов связан с одноименной ему программной функцией – предикатом или действием. Здесь предикаты – функции без параметров, возвращающие булевское значение в зависимости от значения обозреваемой ими ячейки ленты, а действия – функции без параметров, выполняющие то или иной действие по изменению ячейки ленты и передвижению головки машины Тьюринга.
Данный СКА имеет то же множество состояний, что и автомат на рис.3. При этом кроме собственно автоматного отображения, представленного СКА, он реализует еще два отображения – отображение множества предикатов (x1, …, xM) на множество одноименных входных каналов автомата, и множество выходных каналов автомата на множество одноименных действий – y1, …, yN. Например, предикат x3 вернет значение true (значение 1 для одноименного входного сигнала), если в текущей ячейке будет символ 1, а действие y4, которое будет запущено, когда одноименный выходной сигнал автомата примет значение 1, будет соответствовать перемещение головки влево (L) и т.д. и т.п.
Обратим внимание, что СКА не управляет напрямую лентой, а реализует [дополнительные] отображения, связывая сигналы автомата с функциями, определяющими множество операций машины Тьюринга. Это еще раз убеждает, что нет необходимости вводить понятие автоматизированного объекта управления в ситуации, когда достаточно «старомодного», но математически строго понятия отображение.
Сравнивая автоматы на рис. 3 и рис. 4, можно видеть, что СКА не использует команду «*» (см. рис. 1). В подобной ситуации ему достаточно не выдавать сигнал, связанный с данной командой. Кроме того, два и более сигналов (как входных, так и выходных) на одном переходе параллельны. Поэтому, когда возникает конфликт доступа к общим объектам (например, необходимо изменить ячейку и переместить головку) используется соглашение: действия на одном переходе исполняются последовательно в порядке следования их номеров, т.е. действие с большим номером выполняется после действия с меньшим номером. Это соглашение не распространяется на предикаты, т.к. они не изменяют ленту. Так мы делаем автомат более компактным и наглядным (не на-до вводить промежуточные состояния).
В процессе тестирования программы инкремента были выявлены ситуации, когда в процессе работы МТ могут возникнуть проблемы. Во-первых, реальная лента не бесконечна и выход за ее пределы может вызвать «крах» программы. Во-вторых, нужно обязательно указывать начальное положение головки. Без этого, если, например, число находится в произвольном месте ленты, а начальное состояние головки слева от числа и напротив пробела, то головка сразу начнет движение влево. Далее она может выйти за границы ленты, вызвав «крах» программы, или, переместившись, на шаг влево запишет в ячейку 1 и, зависнув, завершит «успешно» работу. Или, если число содержит во всех разрядах 1 и записано с начала ленты, то заключительная попытка переноса 1 в старший разряд вызовет тот же самый «крах».
2.1. Объектная реализация МТ на языке С++
Рассмотрим объектную программную реализацию машины Тьюринга на языке C++ в среде ВКПа, реализующую любую программу для МТ, в том числе и программу вычисления инкремента.
С этой целью создан базовый класс, представляющий любую машину Тьюринга, который и наследуют программные объекты, реализующие ту или иную программу МТ. Данный базовый представлен на листинге 1, а программа, реализующая задачу инкремента, на листинге 2.
Листинг 1. Программная реализация базового класса МТ
Листинг 2. Программа инкремента для машины Тьюринга
2.2. Примеры программ для МТ с реализацией на С++
Рассмотрим пример программы для МТ, которая «выступает как акцептор языка, т.е. она может распознавать язык» из [9]. Ее функция переходов представлена на рис. 5, а эквивалентный ей автомат в форме СКА на рис. 6.
Рис. 5. Функция переходов машины Тьюринга, распознающая язык

Рис. 6. Граф СКА машины Тьюринга, распознающей язык
Блок управления МТ в форме СКА имеет 6 входных и 7 выходных каналов. Про-грамма акцептора включает также соответствующее им число предикатов и действий, которые представлены на рисунке справа от графа автомата. Реализация программы на С++ в среде ВКПа представлена на листинге 3.
Листинг 3. Программа для машины Тьюринга, распознающей язык
На листинге 3 действие y18 представляет вариант программы для МТ в соответствии с подходом SWITCH-технологии. В рамках реализации автоматного программирования среды ВКПа в этом случае вместо автомата на рис. 6 необходимо будет реализовать автомат с одним состоянием, который выдает в цикле сигнал y18. Ему соответствует закомментированная строка таблицы переходов на листинге 3. Для работы автомата по типу SWICH необходимо снять комментарий с данной строки, а остальные строки закомментировать.
Рассмотрим еще один пример программы для машины Тьюринга из [7], где МТ определяется, как «весьма простое расширение модели конечного автомата». В этом случае программа для машины Тьюринга представляет собой конечный список пятерок частично-определенной функции переходов и выходов δ: S×XS×X×Г.
Программа для МТ, находящая наибольший общий делитель (НОД) двух чисел, показана на рис. 7. Эквивалентный ей граф СКА представлен на рис. 8. Заметим, что и здесь не используются команда перезаписи символов. Реализация на С++ представлен листингом 4.

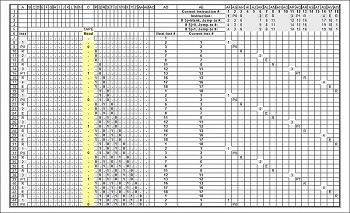
Рис. 7. Граф переходов машины Тьюринга, вычисляющей НОД двух чисел, и несколько ее конфигураций при обработке пары чисел
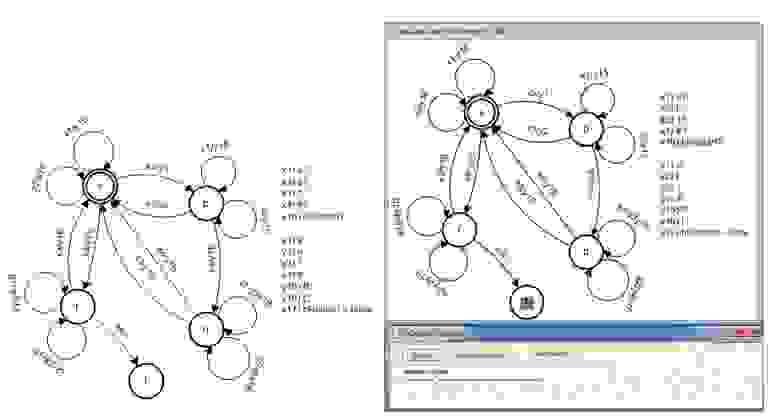
Рис. 8. Граф СКА, эквивалентный графу на рис. 7
Листинг 4. Программа для машины Тьюринга нахождения НОД двух чисел
В заключение еще одна программа для МТ от разработчиков SWITH-технологии, рассмотренная в статье [11], где приведена задача распознавание скобок в двух варианта. Один в форме автомата Мили, второй – смешанный автомат (соответственно на рис. 9 и рис. 11). Соответствующие им структурные автоматы приведены на рис. 10 и рис. 12. Реализацию программы на С++ демонстрирует листинг 5.

Рис. 9. Распознавание скобок произвольной глубины. Граф переходов Мили
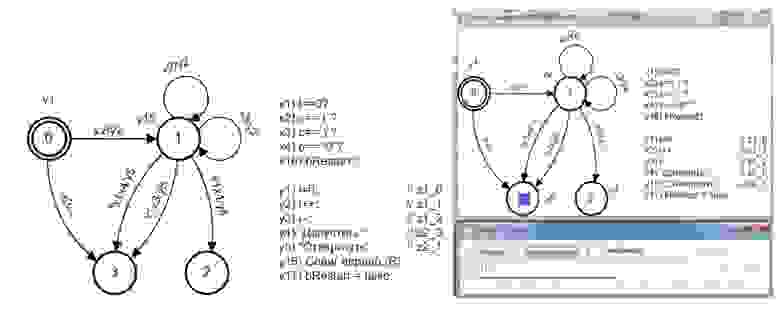
Рис. 10. Распознавание скобок произвольной глубины. Граф СКА Мили
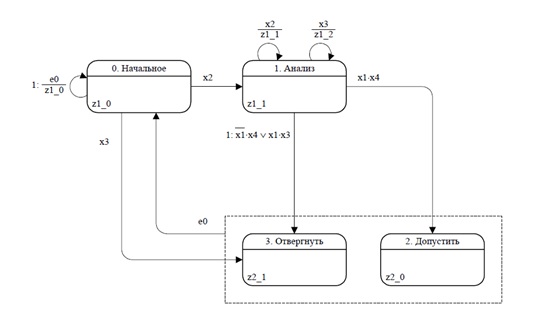
Рис. 11. Распознавание скобок произвольной глубины. Граф переходов смешанного автомата

Рис. 12. Распознавание скобок произвольной глубины. Граф СКА переходов сме-шанного автомата
Листинг 5. Программа для машины Тьюринга распознавания вложенности скобок
Поскольку автомат на рис. 12 отказался работать, то было решено перейти к автомату на рис. 9. Эквивалентный ему автомат в форме СКА, показан на рис. 10. Правда, формально это тоже смешанный автомат, у которого от первой реализации (рис. 12) был оставлен сигнал при состоянии «0» и сигнал y15 при состоянии «1». Первый необходим при начальной установке, а сигнал y15 реализует смещение головки вправо в целях чтения очередного символа ленты. В остальном СКА соответствует автомату Мили на рис. 9.
После того, как автомат на рис. 10 был успешно протестирован, вернулись к автомату на рис. 11. И стало понятно, что у него лишним является сигнал z1_1 при состоянии «1»(у автомата на рис. 12 это сигнал y2). Проблема в том, что он, обнаружив «левую скобку», наращивает счетчик на две единица, а при обнаружении «левой скобки» не изменяет его совсем. Так, при обнаружении «левой скобки» он вызывается дважды – один раз на петле,, помеченной x2/y2, а второй раз при входе в состояние. А при обнаружении «правой скобки» счетчик сначала на петле уменьшается, а затем при входе в состояние увеличивается.
Причина такой работы управления МТ, в неверной трактовке авторами функционирования автомата типа Мура. Видимо, они полагают, что сигнал при состоянии у автомата Мура исполняется только при входе в это состояние (см. переход из состояния «0» в «1»), а на самом деле он выдается всякий раз при входе в это состояние. В том числе и при переходе по петле. Таким образом, мы имеет дело не с ошибкой (кто не ошибался?), а с более серьезной проблемой — неверной трактовкой в рамках SWITH-технологии функционирования автоматов типа Мура. Тестирование эквивалентной модели это и показало.
Подводя итог, можно сказать, что нет формальных отличий тьюрингового программирования от автоматного, т.к. машина Тьюринга – это абстрактная модель автоматных программ. Просто в последнем случае используется более широкий набор операторов и структур данных (памяти). Теперь можно уверенно ответить и на вопрос, чем отличается машина Поста, как модель обычных программ, от машины Тьюринга — модели автоматных программ. Моделью управления и лишь только ею, т.к. остальное – память и операторы могут быть одними и теми же.
Следовательно, обычное программирование отличается от программирования автоматного только одним – моделью управления. Таким образом, пока для реализации автоматов используются обычные операторы управления типа switch и им подобные нельзя, строго говоря, такое программирование считать автоматным. Это может быть имитация автоматов с утратой их определенных свойств и не более того.
Итак, давая определение понятий автоматной программы и автоматного программирования, говорить надо не об «автоматизированных объектах управления», а о программах и только программах, имеющих управление в форме классического конечного автомата.
И еще интересный факт, на который хотелось бы обратить внимание. В начале 2000-х годов, авторы озвучили свое понимание автоматного программирования на широкую аудиторию. Их статьи по поводу абстрактных машин были напечатаны в журнале «Мир ПК» №2 за 2002 г. [11, 12, 13]. Можно утверждать, что годы на убеждения сторон не повлияли. Хотя, возможно, это отражает только степень их уверенности в выбранных решениях.
Например, в «новую лекцию по автоматному программированию» Шалыто А.А. по сравнению с предыдущей «лекцией со слайдами» (десятилетней давности) добавлено лишь видео примера на базе «автоматного пакета» Stateflow. Казалось бы, это подтверждает правоту идей Шалыто А.А., т.к. то, что не удалось реализовать в рамках UniMod (проект, похоже, «заморожен»), воплотили разработчики Stateflow. И, наверное, не так уж важно кто это сделал…
Однако, на момент публикации упомянутых статей авторам SWITCH-технологии уже была известна критика в ее адрес. Это не было тайной, т.к. с ней можно было ознакомиться на сайте SoftCraft [14]. На нем же были созданы разделы, посвященные автоматному программированию вообще и SWITH-технологии и КА-технологии в частности. Позиции авторов обсуждались на форуме сайта (он был на тот момент открыт). Но все так и остались при своем мнении.
Итоги на текущий момент таковы. Критика, высказанная в отношении SWITH-технологии когда-то давно, актуальна и на текущий момент. Она же относится и к пакету Stateflow. В SWITH-технологии как не было, так и нет четкого определения автоматного программирования, не изменился подход к реализации автоматов, сама модель не является классической, нет модели параллельных вычислений и т.д. и т.п. Без устранения этих проблем подобное автоматное программирование в лучшем случае претендует на достаточно ограниченную роль.
Причины отмеченных выше проблем довольно ясны: игнорируется теория программ, забыта теория автоматов, хотя о самих автоматах и об их замечательных свойствах сказано много хороших и правильных слов. Но по факту это другие автоматы. Автор убежден в сомнительности непродуманных попыток создавать оригинальные модели. Речь о синхронных, реактивных и других моделях. Они могут быть удобны при решении узкого класса задач и не более того. Но серьезнее то, что они выпадают из теории автоматов, не имея при этом собственной теории. А модель вне теории беспомощна, а потому фактически бессмысленна.