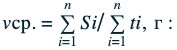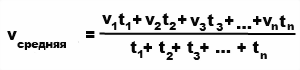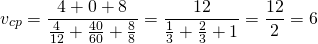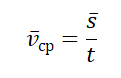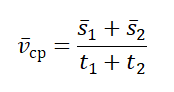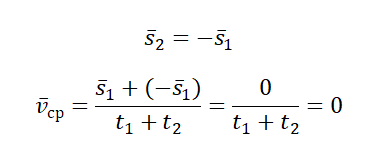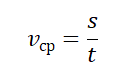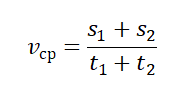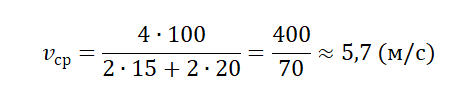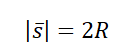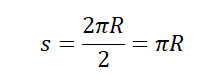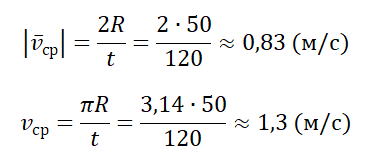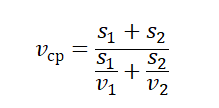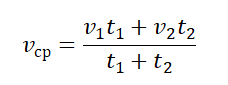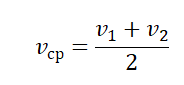Как считать среднюю скорость автомобиля

Способы нахождения средней скорости в физике

Основные понятия и законы кинематики

Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.

Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.

Тело отсчета — это тело, относительно которого рассматривают положение других тел.

Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.

Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.

Траектория движения делится на два типа:

Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.

Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.

Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.

Определение средней скорости

Рассчитать среднюю скорость можно по следующей формуле:

Определение средней путевой скорости

Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.

Формула средней путевой скорости выглядит так:

Примеры решения задач

Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.

В условии сказано о трех участках пути.

ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3

Участки пути мы можем вычислить и посчитать следующим образом:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч

Ответ: средняя скорость составляет 88 км/ч.

Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?

ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч

Ответ: средняя скорость автомобиля составляет 40 км/ч.

Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.

Искать среднюю скорость будем как во второй задаче.

Источник

Вычисление средней скорости движения в физике: расчёты и формулы

Содержание:

Под средней скоростью движения какого-либо тела понимают отношение пройденного расстояния к временному промежутку, который был затрачен на его преодоление. Определение средней скорости может понадобиться в случае, когда в процессе перемещения тела на разных участках его скорость изменялась. Неважно в каком направлении совершалось движение и изменялось ли оно с течением времени. Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.

Как найти среднюю скорость тела?

Пример. Автомобиль всего проехал 1 километр и 200 метров. После каждых 400 м он изменял скорость движения. Первые 400 метров он двигался со скоростью 20 км/ч, потом со скоростью 40 км/ч, 50 км/ч и последний участок проехал на скорости 35 км/ч. Определение средней скорости движения производим так:

В любом другом случае вычисление средней скорости в физике производят более сложным путем по формуле:

Пример задачи на вычисление средней скорости в физике

Сначала найдем путь, который был пройден за каждый из промежутков времени:

Далее пишется вышеприведенная формула в более привычном виде, как обычно, подставляются необходимые данные и определяется средняя скорость:

Средняя скорость при равноускоренном движении

На практике очень часто встречаются задачи, когда вычисление средней скорости необходимо производить для случая, когда тело, двигаясь с какой-то начальной скоростью, с течением времени начало ускоряться и в конце пути достигло какой-то новой скорости. Тогда следует использовать формулу, которая выражает среднюю скорость через величину ускорения:

vcp. = v0 + \frac < at > < 2 >, где:

Пример. Двигаясь с начальной скоростью 160 м/с, самолет в течение двух минут ускорял свое движение на 1,5 м/с2. Какова его средняя скорость за этот промежуток времени?

vcp. = 160 + \frac < 1,5 * 120 > < 2 >= 250 м/с

Источник

Как находить среднюю скорость

Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

На примерах посмотрим, как находить среднюю скорость.

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.

Находим все время движения: 2+3=5 часов.

Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.

Переведем минуты в часы: 30 минут = 0,5 часа.

Найдем весь пройденный автомобилем путь:

2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.

Находим все время движения:

Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:

3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

Найдем весь путь велосипедиста:

3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения:

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

195 Comments

самый лучший сайт по математике спасибо огромное

Илья, спасибо за теплые слова!

Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно

Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.

Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?

Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.

Источник

Неравномерное движение и средняя скорость

теория по физике 🧲 кинематика

Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.

Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.

Средняя векторная скорость

Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.

v _ср — средняя векторная скорость, s — перемещение тела, совершенное за время t

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.

Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:

Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.

Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:

Средняя скалярная скорость

Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.

v_ср — средняя путевая скорость, s — путь, пройденный телом за время t

Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:

Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.

У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:

Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:

Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.

Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:

Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:

Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:

Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.

Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:

Источник

Как найти среднюю скорость. Пошаговая инструкция

Есть средние величины, неправильное определение которых вошло в анекдот или в притчу. Любые неверно произведённые расчёты комментируются расхожей общепонятной ссылкой на такой заведомо абсурдный результат. У каждого, к примеру, вызовет улыбку саркастического понимания фраза «средняя температура по больнице». Однако те же знатоки нередко, не задумываясь, складывают скорости на отдельных отрезках пути и делят подсчитанную сумму на число этих участков, чтобы получить столь же бессмысленный ответ. Напомним из курса механики средней школы, как найти среднюю скорость правильным, а не абсурдным способом.

Аналог «средней температуры» в механике

Простые «формулы» расчёта величин при равномерном движении

И для всего пройденного пути, и для отдельных его участков в случае усреднения скорости справедливы соотношения, написанные для равномерного движения:

То есть для нахождения искомой величины v с использованием соотношения (3) нам нужно точно знать две другие. Именно решая вопрос, как найти среднюю скорость движения, мы прежде всего должны определить, каков весь пройденный путь S и каково всё время движения t.

Математическое обнаружение скрытой ошибки

Явное подтверждение ошибки «в числах»

Когда среднее арифметическое «не подводит»

Если задача формулируется так: «За равные промежутки времени тело двигалось сначала со скоростью v₁, затем v₂, v₃ и так далее», быстрый ответ на вопрос, как найти среднюю скорость, может быть найден неправильным способом. Предоставим читателю самостоятельно в этом убедиться, просуммировав в знаменателе равные промежутки времени и воспользовавшись в числителе v_ср соотношением (1). Это, пожалуй, единственный случай, когда ошибочный метод приводит к получению корректного результата. Но для гарантированно точных расчётов нужно пользоваться единственно правильным алгоритмом, неизменно обращаясь к дроби v_ср = S : t.

Алгоритм на все случаи жизни

Для того чтобы наверняка избежать ошибки, при решении вопроса, как найти среднюю скорость, достаточно запомнить и выполнить простую последовательность действий:

В статье рассмотрены простейшие случаи, когда исходные данные приводятся для равных долей времени или равных участков пути. В общем случае соотношение хронологических промежутков либо пройденных телом расстояний может быть самым произвольным (но при этом математически определённым, выраженным конкретным целым числом или дробью). Правило обращения к соотношению v_ср = S : t абсолютно универсально и никогда не подводит, сколь бы сложные на первый взгляд алгебраические преобразования ни приходилось выполнять.

Напоследок отметим: для наблюдательных читателей не осталась незамеченной практическая значимость использования верного алгоритма. Правильно рассчитанная средняя скорость в приведённых примерах оказалась несколько ниже «средней температуры» на трассе. Поэтому ложный алгоритм для систем, фиксирующих превышения скорости, означал бы большее число ошибочных постановлений ГИБДД, высылаемых в «письмах счастья» водителям.

Источник