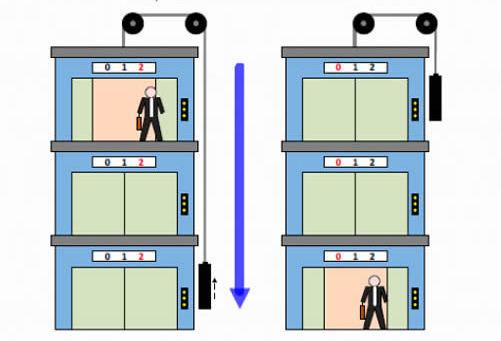
Как создается равномерное движение двух грузов на машине атвуда
НА МАШИНЕ АТВУДА



Задание: Экспериментально проверить законы равномерного и равноускоренного движений. Определить ускорение свободного падения с предельной относительной погрешностью e, не превышающей 5 %.
Оборудование и принадлежности: установка для проведения измерений, набор грузов, весы.
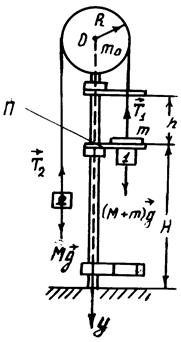 Рис. 1 Рис. 1 |
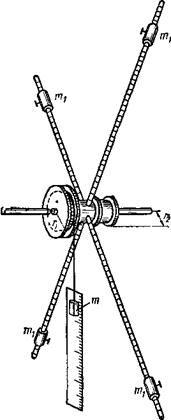
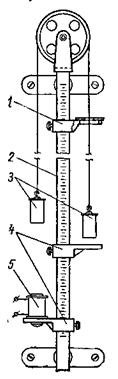
Для проверки законов кинематики и определения ускорения свободного падения в работе используется машина Атвуда, схема устройства которой показана на рис. 1.
Через блок перекинута нить с двумя одинаковыми грузами 1 и 2 на концах, масса каждого груза М. В этом случае система находится в равновесии. Если на один из грузов положить перегрузок малой массы m, то грузы будут двигаться равноускоренно. На пути груза с перегрузком установлена кольцевая платформа “П”. На кольцевой платформе перегрузок снимается и дальше грузы движутся равномерно.
Для изучения равноускоренного движения используются перегрузки меньшего диаметра, которые вместе с грузом проходят через кольцевую платформу. Расстояния h и H (рис. 1) можно изменять передвижением верхней и средней муфт.
Электромагнит установки при помощи фрикционной муфты при не включенной кнопке “пуск” удерживает систему ролика с грузами в состоянии покоя.
Общие сведения. Из определения скорости и ускорения материальной точки:
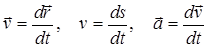
следуют выражения для радиус-вектора, пути и вектора скорости:
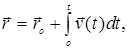
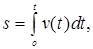
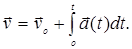
Из уравнений (3) и (4) следует, в частности, что при равномерном движении (а = 0) вектор скорости остаётся постоянным 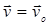
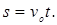
При равноускоренном (a = const) движении без начальной скорости(vo = 0) получаем:
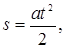
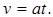
Исключая время t из соотношений (6) и (7), найдём связь пути, скорости и ускорения материальной точки при равноускоренном движении без начальной скорости:
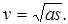
При изучении кинематики материальной точки полезно использовать графический метод. На графике зависимости s(t) при равномерном движении (уравнение (5)) скорость материальной точки равна тангенсу угла наклона прямой графика к оси абсцисс t. На графике зависимости v(t) при прямолинейном равноускоренном движении материальной точки ускорение равно тангенсу угла наклона графика (прямой линии) к оси абсцисс t. Это можно использовать для графического определения скорости и ускорения материальной точки из опыта.
При небольших скоростях (v«c) движения материальной точки постоянной массы её ускорение, по второму закону Ньютона:

Угловое ускорение твердого тела определяется соотношением (основной закон динамики вращательного движения твёрдого тела):
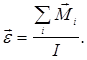
Теория работы. Если на груз 1 положить перегрузок массой m, то он начнёт двигаться с ускорением a, которое можно найти с помощью законов динамики для грузов 1, 2 и для блока:
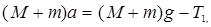
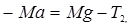
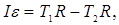
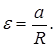
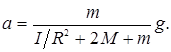
Момент инерции блока 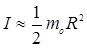
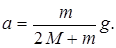
Движение грузов на машине Атвуда описывается соотношениями (5)-(8), в которых ускорение a задаётся формулой (16), а путь s – это расстояние, пройденное грузом 1.
Если груз 1 на участке h движется равноускоренно, а на участке H – равномерно (рис. 1), то его движение описывается уравнениями (5) и, (8) соответственно, которые в данном случае принимают вид:
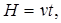
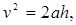
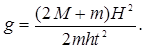
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
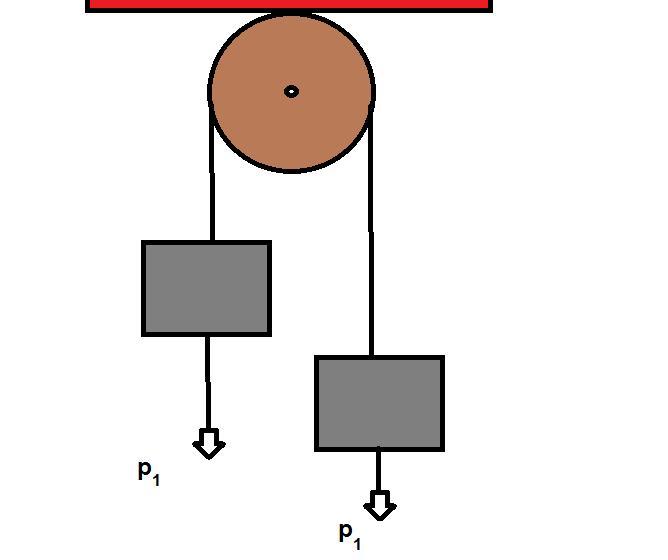
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Краткое знакомство и машиной Атвуда


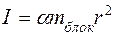

Пусть правый груз опустился на расстояние h. Тогда изменение потенциальной энергии сиcтемы: 
Потенциальная энергия переходит в кинетическую энергию поступательного и вращательного движения (работой по преодолению сил трения пренебрегаем): 
где 


Если пренебречь моментом инерции блока, то формула (2) примет вид: 
Связь между угловым ускорением блока и линейным ускорением грузов получена в предположении, что скольжение нити по блоку отсутствует.
Итак, система при наличии перегрузка будет двигаться с линейным ускорением, меньшим, чем ускорение свободного падения. Если перегрузок снять во время движения, то последующее движение будет равномерным со скоростью. Равной скорости в момент снятия перегрузка.
Таким образом, экспериментальная установка позволяет получить равномерное и равноускоренное движения грузов. Однако из-за наличия сил трения проверяемые равенства будут таковыми лишь приближенно.
КРАТКАЯ ТЕОРИЯ ВОПРОСА.
В равномерном движении путь S пропорционален затраченному на его прохождение промежутку времени t:

В равнопеременном движении ускорение а характеризует изменение скорости в единицу времени. Если движение равноускоренное, то скорость меняется по закону:

Путь при равноускоренном движении с начальной скоростью V0:

Тогда при V0=0 путь пропорционален квадрату времени:

а скорость пропорциональна времени:

Уравнения (1) – (5) являются основными в кинематике.
1. Движение каких объектов происходит в машине Атвуда? Каков характер их движения?
2. Как создается равномерное движение грузов на машине Атвуда?
3. Каковы условия равноускоренного движения грузов? Чем пренебрегают, полагая их движение таковым?
4. Как с помощью машины Атвуда и дополнительных приспособлений и средств (каких?) можно измерить пройденный путь и затраченное на его прохождение время?
5. Какой величине пропорционален путь в случае равноускоренного и равномерного движений? Иначе: Линейной функцией какого аргумента может считаться путь в случае равноускоренного и равномерного движений? Иначе: Что следует откладывать по оси х при изучении закона движения в обоих случаях, чтобы графиком была прямая?
6. Запишите выражение для внешней силы, сообщающей системе грузов в машине Атвуда ускорение.
7. Что называется законом движения? Запишите законы равномерного и равноускоренного движений (для пути и для координаты).
8. Запишите расчетную формулу для ускорения. Чем пришлось пренебречь для ее получения?
Содержание экспериментальных заданий
Задание1. Проверка формулы (4) зависимости пути от времени.
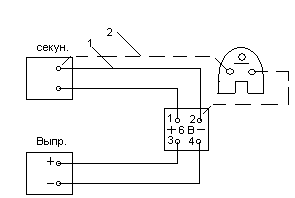
1) Соберите цепь по схеме (рис.2), соединив машину Атвуда с секундомером и источником постоянного тока. Правый груз с перегрузком установите нижней поверхностью против нулевой отметки шкалы и зафиксировать включением электромагнита 5 (рис.1). Если разомкнуть цепь электромагнита, то грузы начнут двигаться.
2) Установите приемный столик 4 на расстоянии S от нулевой отметки. В начале опыта чашка столика должна быть поднята. В конце пути S груз ударяет о чашку столика, она опускается и секундомер прекращает отсчет времени t. Т.е. показание секундомера есть время движения грузов на пути S.
3) Произведите 3 опыта для каждого положения столика, сняв три показания секундомера t1, t2, t3. Для вычислений используйте их среднее значение tср..
4) Получите ряд соответствующих пар значений (S,t), (не менее трех пар), занесите результаты измерений и вычислений в таблицу 1:
5) Из формулы (4) выразите ускорение. Усреднив значения из предпоследнего столбца, вычислите ускорение грузов, считая их движение равноускоренным.
6) Постройте график зависимости S(t 2 ): укажите на координатной плоскости экспериментальные точки; осуществите их линейную аппроксимацию. Сделайте вывод о степени близости исследуемого движения к равнопеременному виду движения.
Задание 2. Проверка формулы (5) зависимости скорости от времени.
1) Используйте прежнюю схему. На правом грузе поместите перегрузок и обеспечьте равновесие системы с помощью электромагнита.
2) Произведите измерение промежутков времени 
3) Переместите приемный столик в положение 4, соответствующее наинизшей точке по шкале.
4) Устанавливая подвижное кольцо поочередно в положения 1,2 и 3 между грузом и столиком и используя соединение согласно рис.1, измерьте время равномерного движения груза между каждой из точек 1,2 или 3 и точкой 4. Таблица 2
| i=1 | i=2 | i=3 |
 | ||
| Si+3 | ||
 | ||
| Vi | ||
| ai |
Запишите расстояния 

5) Считая, что скорость равномерного движения груза после снятия перегрузка равна конечной скорости равноускоренного движения в момент снятия перегрузка, получим равенства: 
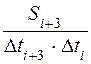
6) Сравнивая значения из последней строки таблицы 2, сделать вывод о характере движения грузов до снятия перегрузка. Укажите причины выявленных отклонений.
Задание 3. Проверка формулы (1) зависимости пути от времени.
1) Используйте схему с подвижным кольцом. На правом грузе поместите перегрузок и обеспечьте равновесие системы с помощью электромагнита (левый груз находится внизу).
2) Расположите подвижное кольцо для снятия перегрузка на расстоянии 30-40 см от верхнего края штанги. Нижнюю подставку-столик закрепляйте поочередно на расстояниях 60, 70 и 80 см от верхнего края.
3) Выключите электромагнит. Обеспечьте включение секундомера в момент снятия перегрузка. Когда правый груз ударяется о подставку, секундомер должен выключиться. Таким образом получите значения интервалов времени движения правого груза от кольца до каждого из 3-х положений подставки-столика.
4) Занесите в таблицу 3 проходимые грузом расстояния и соответствующую длительность движения, а также их отношения:
| № п/п | S, м | 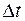 , с , с | S/Dt, м/с | Vср., м/с |
| 1. | ||||
| 2. | ||||
| 3. |
5) Проверьте, выполняется ли условие:
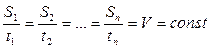
Сделайте вывод с указанием причин необходимости приближения.
Задание 4. Проверка второго закона Ньютона.
При проверке этого закона необходимо, чтобы движущаяся масса оставалась постоянной. В то же время внешняя сила, приложенная к системе, будет меняться, а с ней и ускорение движения системы. Т.е. необходимо измерить промежутки времени ускоренного движения системы при различных распределениях перегрузков в ней.
Например, при измерении на правый груз кладут два перегрузка 



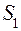

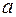


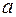
При неизменном исходном положении грузов и одном и том же положении приемного столика будем иметь один и тот же путь. Тогда отношение ускорений согласно (4) обратно пропорционально отношению квадратов соответствующих промежутков времени движения.
Для двух различных случаев согласно второму закону Ньютона будем иметь 


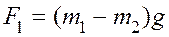
В этом случае выполнение соотношения 

Заполните таблицу 4:
Таблица 4
| m1 | m2 | m1+m2 | m1-m2 | t1 |  | t2 |  |  |  |
Сделать вывод на основе полученных вами числовых данных.
Вопросы к отчету.
1. Перечислить и дать определение всем кинематическим характеристикам движения материальной точки (путь, перемещение, скорость, мгновенная скорость, ускорение, линейное и угловое и т.д.).
2. Какие уравнения служат для описания движения?
3. Что называется динамическим уравнением движения?
4. Как можно определить момент инерции блока, пользуясь измерениями, в данной работе?
5. Относительно какой системы отсчета рассматривается движение грузов?
6. Сформулируйте законы Ньютона.
7. Выведите формулу (6) и покажите, как она подтверждает второй закон Ньютона.
8. Подсчитайте силу натяжения нити при равноускоренном и при равномерном движении грузов.
9. Выведите формулу для ускорения, учитывая силу трения.
Лабораторная работа № 2.2.
Изучение вращательного движения на крестообразном
Цель работы: изучить законы вращательного движения твердого тела и познакомиться с методом их экспериментальной проверки; определить моменты инерции крестовины и груза.