Кпд тепловой машины равен 25 какую работу совершила машина если при сгорании топлива выделилось
КПД теплового двигателя. Решение задач. 8класс
Данная презентация поможет при решениии задач по теме КПД в 8 классе
Просмотр содержимого документа
«КПД теплового двигателя. Решение задач. 8класс»
КПД теплового двигателя Решение задач 8класс
1. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 230 кДж, а отдает холодильнику количество теплоты, равное 100 кДж. Определите полезную работу двигателя за это время.
2. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 120кДж, и совершает при этом полезную работу 20 кДж. Определите КПД такого двигателя.
3. КПД теплового двигателя равен 45%. Какую полезную работу совершит двигатель, если он получит от нагревателя количество теплоты, равное 600 кДж?
4. Количество теплоты, полученное от нагревателя тепловым двигателем, равно 10 кДж. За тоже время он отдает холодильнику количество теплоты, равное 5 кДж. Найдите работу, совершенную двигателем, и КПД этого двигателя.
5. На древесном угле массой 17г нагревают воду. Взяли 200г воды и нагрели от 15 0 С до 57 0 С. Найти КПД тепловой установки.
продолжение на следующем слайде

КПД теплового двигателя
Содержание
В данном разделе вы уже познакомились с устройством и принципом работы двух видов теплового двигателя: двигателя внутреннего сгорания и паровой турбины. Используя эти механизмы, мы совершаем какую-то работу. Очевидно, что работа будет совершаться за счет энергии, которая выделяется при сгорании топлива. Но большая часть этой энергии теряется в окружающей среде. То есть, эта часть энергии не используется полезно.
Следовательно, и работу таких механизмов тогда нужно рассчитывать специальным образом. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. В данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.
Полезная работа теплового двигателя
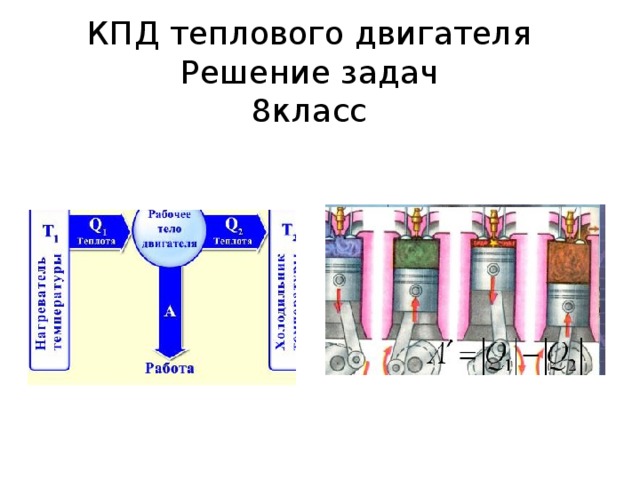
Для того чтобы судить о полезной работе теплового двигателя, обратимся еще раз к его устройству. Если рассматривать его принцип работы, то устройство любого теплового двигателя можно представить в виде простой схемы (рисунок 1).
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника.
Рабочим телом является газ или пар. Например, в паровой турбине – это пар, в газовой – газ, в двигателе внутреннего сгорания – смесь паров бензина и воздуха.
Этот газ получает некоторое количество теплоты $Q_1$ от нагревателя. Под нагревателем подразумевается не какое-то специальное механическое устройство, как можно подумать. Нагреватель в схеме теплового двигателя – это горящее топливо.
Газ нагревается и расширяется. Так он совершает работу $A_п$, используя свою внутреннюю энергию.
Но важно понимать, что часть этой внутренней энергии $Q_2$ не совершает какую-то полезную для нас работу. Она передается вместе с отработанным паром или выхлопными газами атмосфере – холодильнику.
В качестве холодильника может использоваться резервуар с водой. Отработавший пар будет в таком случае приносить дополнительную пользу – нагревать воду для ее дальнейшего использования. Но этот процесс уже требует отдельного рассмотрения.
Итак, нас интересует именно та часть энергии топлива, выделяемая при его сгорании, которая превращается в полезную работу. От величины этой части энергии зависит экономичность двигателя.
Для этой характеристики мы вводим новое понятие – коэффициент полезного действия (КПД) теплового двигателя.
КПД теплового двигателя
Коэффициент полезного действия (КПД) теплового двигателя – это отношение совершенной полезной работы двигателя к энергии, полученной от нагревателя.
КПД теплового двигателя также как и КПД простейших механизмов, изученных вами в прошлом курсе, обозначается греческой буквой “эта” – $\eta$ и выражается в процентах.
Формула для расчета КПД теплового двигателя имеет следующий вид:
Средние значения КПД различных тепловых двигателей
В таблице 1 представлены средние значения КПД некоторых двигателей.
| Двигатель | КПД, % |
| Паровой двигатель | 8 |
| Двигатель внутреннего сгорания | 18 – 40 |
| Газовая турбина | 25 – 30 |
| Паровая турбина | 40 |
| Дизельный двигатель | 40 – 44 |
| Реактивный двигатель на жидком топливе | 47 |
Таблица 1. КПД различных двигателей
Одной из важнейших технических задач при проектировании двигателей является повышение значения КПД.
Примеры задач
Дано:
$\eta = 30 \%$
$Q_1 = 600 \space кДж$
СИ:
$6 \cdot 10^5 \space Дж$
Посмотреть решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Чтобы использовать эту формулу необходимо значение КПД, выраженное в процентах перевести в дробь:
$\eta = 30 \% = 0.3$
Дано:
$Q_1 = 155 \space Дж$
$Q_2 = 85 \space Дж$
Посмотреть решение и ответ
Решение:
Используем формулу для расчета КПД:
$\eta = \frac
Дано:
$A_п = 2.3 \cdot 10^4 \space кДж$
$m = 2 \space кг$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$2.3 \cdot 10^7 \space Дж$
Посмотреть решение и ответ
Решение:
В нашем случае нагревателем является бензин. Мы знаем его массу и удельную теплоту сгорания, поэтому можем рассчитать количество теплоты, выделенное при его сгорании по формуле:
$Q = Q_1 = qm$.
$Q_1 = 2 \space кг \cdot 4.6 \cdot 10^7 \frac<Дж> <кг>= 9.2 \cdot 10^7 \space Дж$.
Решение задач на КПД теплового двигателя
Содержание
В данном уроке мы разберем решение задач, используя формулы, приведенные выше.
Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.
Задача №1
Дано:
$m = 300 \space г$
$\Delta t = 200 \degree C$
$c = 460 \frac<Дж><кг \cdot \degree C>$
СИ:
$m = 0.3 \space кг$
Показать решение и ответ
Решение:
Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 – t_1) = cm \Delta t$.
Рассчитаем эту энергию:
$Q = 460 \frac<Дж> <кг \cdot \degree C>\cdot 0.3 \space кг \cdot 200 \degree C = 27 \space 600 \space Дж = 27.6 \space кДж$.
Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 \space кДж$.
Задача №2
Дано:
$t = 1 \space ч$
$N = 733 \space Вт$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$t = 3600 \space с$
Показать решение и ответ
Решение:
Мощность по определению:
$N = \frac
Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
$A_п = Nt$,
$A_п = 733 \space Вт \cdot 3600 \space с = 2 \space 638 \space 800 \space Дж \approx 0.26 \cdot 10^7 \space Дж$.
По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.
Выразим отсюда массу угля и рассчитаем ее:
$m = \frac$,
$m = \frac<0.26 \cdot 10^7 \space Дж><2.7 \cdot 10^7 \frac<Дж><кг>> \approx 0.1 \space кг \approx 100 \space г$.
Задача №3
Дано:
$Q_1 = 120 \space кДж$
$A_п = 30 \space кДж$
СИ:
$Q_1 = 120 \cdot 10^3 \space Дж$
$A_п = 30 \cdot 10^3 \space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Задача №4
Дано:
$t = 30 \space мин$
$Q_1 = 460 \space МДж$
$Q_2 = 280 \space МДж$
СИ:
$t = 1800 \space с$
$Q_1 = 460 \cdot 10^6 \space Дж$
$Q_2 = 280 \cdot 10^6 \space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = =\frac
$A_п$ – полезная работа,
$Q_1$ – количество теплоты, полученное от нагревателя,
$Q_2$ – количество теплоты, отданное холодильнику.
Величина работы также присутствует в определении мощности:
$N = \frac
Когда мощность определяется полезной работой, мы называем ее полезной мощностью.
Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = \frac
$N = \frac<460 \cdot 10^6 \space Дж – 280> <1800 \space с>= \frac<180 \cdot 10^6 \space Дж> <1800 \space с>= 0.1 \cdot 10^6 \space Вт = 100 \space кВт$.
Задача №5
Дано:
$N = 367 \space кВт$
$t = 1 \space ч$
$Q_1 = 6720 \space МДж$
СИ:
$N = 367 \cdot 10^3 \space Вт$
$t = 3600 \space с$
$Q_1 = 6720 \cdot 10^6 \space Дж$
Показать решение и ответ
Решение:
Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 – Q_2$.
Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 – A_п$.
Совершенную работу мы можем определить через мощность:
$N = \frac
$A_п = Nt$.
Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 – Nt$.
Рассчитаем эту энергию:
$Q_2 = 6720 \cdot 10^6 \space Дж – 367 \cdot 10^3 \space Вт \cdot 3600 \space с = 6720 \cdot 10^6 \space Дж – 1321.2 \cdot 10^6 \space Дж = 5398.8 \cdot 10^6 \space Дж \approx 5400 \space МДж$.
Задача №6
Дано:
$\upsilon = 20 \frac<км><ч>$
$s = 100 \space км$
$m = 1 \space кг$
$\eta = 22 \% = 0.22$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$\upsilon \approx 5.6 \frac<м><с>$
$s = 100 \cdot 10^3 \space м$
Показать решение и ответ
Решение:
Мощность по определению:
$N = \frac
Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$\eta = \frac
Подставим в формулу для расчета КПД:
$\eta = \frac
Выразим отсюда полезную работу:
$A_п = \eta \cdot qm$.
Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = \frac<\upsilon>$.
Задача №7
Дано:
$N = 36.6 \space кВт$
$t = 1 \space ч$
$m = 10 \space кг$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 36.6 \cdot 10^3 \space Вт$
$t = 3600 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Задача №8
Дано:
$N = 220 \space кВт$
$t = 8 \space ч$
$\eta = 15 \% = 0.15$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 220 \cdot 10^3 \space Вт$
$t = 28.8 \cdot 10^3 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД:
$\eta = \frac
Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$\eta = \frac
Выразим отсюда массу каменного угля:
$m = \frac$.
Задача №9
Дано:
$Q_1 = 12.57 \space МДж$
$t = 1 \space ч$
$N = 735 \space Вт$
СИ:
$Q_1 = 12.57 \cdot 10^6 \space Дж$
$t = 3600 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$\eta = \frac
$\eta = \frac<735 \space Вт \cdot 3600 с> <12.57 \cdot 10^6 \space Дж>\cdot 100 \% \approx 21 \%$.
Задача №10
Дано:
$N = 367 \space кВт$
$m = 60 \space т$
$\eta = 30 \% = 0.3$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 367 \cdot 10^3 \space Вт$
$m = 60 \cdot 10^3 \space кг$
Показать решение и ответ
Решение:
Формула для расчета КПД теплового двигателя:
$\eta = \frac
Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$\eta = \frac
Выразим отсюда время, за которое была совершена полезная работа:
$t = \frac
Решение задач на КПД теплового двигателя
Содержание
В данном уроке мы разберем решение задач, используя формулы, приведенные выше.
Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.
Задача №1
Дано:
$m = 300 \space г$
$\Delta t = 200 \degree C$
$c = 460 \frac<Дж><кг \cdot \degree C>$
СИ:
$m = 0.3 \space кг$
Показать решение и ответ
Решение:
Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 – t_1) = cm \Delta t$.
Рассчитаем эту энергию:
$Q = 460 \frac<Дж> <кг \cdot \degree C>\cdot 0.3 \space кг \cdot 200 \degree C = 27 \space 600 \space Дж = 27.6 \space кДж$.
Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 \space кДж$.
Задача №2
Дано:
$t = 1 \space ч$
$N = 733 \space Вт$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$t = 3600 \space с$
Показать решение и ответ
Решение:
Мощность по определению:
$N = \frac
Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
$A_п = Nt$,
$A_п = 733 \space Вт \cdot 3600 \space с = 2 \space 638 \space 800 \space Дж \approx 0.26 \cdot 10^7 \space Дж$.
По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.
Выразим отсюда массу угля и рассчитаем ее:
$m = \frac$,
$m = \frac<0.26 \cdot 10^7 \space Дж><2.7 \cdot 10^7 \frac<Дж><кг>> \approx 0.1 \space кг \approx 100 \space г$.
Задача №3
Дано:
$Q_1 = 120 \space кДж$
$A_п = 30 \space кДж$
СИ:
$Q_1 = 120 \cdot 10^3 \space Дж$
$A_п = 30 \cdot 10^3 \space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Задача №4
Дано:
$t = 30 \space мин$
$Q_1 = 460 \space МДж$
$Q_2 = 280 \space МДж$
СИ:
$t = 1800 \space с$
$Q_1 = 460 \cdot 10^6 \space Дж$
$Q_2 = 280 \cdot 10^6 \space Дж$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = =\frac
$A_п$ – полезная работа,
$Q_1$ – количество теплоты, полученное от нагревателя,
$Q_2$ – количество теплоты, отданное холодильнику.
Величина работы также присутствует в определении мощности:
$N = \frac
Когда мощность определяется полезной работой, мы называем ее полезной мощностью.
Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = \frac
$N = \frac<460 \cdot 10^6 \space Дж – 280> <1800 \space с>= \frac<180 \cdot 10^6 \space Дж> <1800 \space с>= 0.1 \cdot 10^6 \space Вт = 100 \space кВт$.
Задача №5
Дано:
$N = 367 \space кВт$
$t = 1 \space ч$
$Q_1 = 6720 \space МДж$
СИ:
$N = 367 \cdot 10^3 \space Вт$
$t = 3600 \space с$
$Q_1 = 6720 \cdot 10^6 \space Дж$
Показать решение и ответ
Решение:
Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 – Q_2$.
Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 – A_п$.
Совершенную работу мы можем определить через мощность:
$N = \frac
$A_п = Nt$.
Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 – Nt$.
Рассчитаем эту энергию:
$Q_2 = 6720 \cdot 10^6 \space Дж – 367 \cdot 10^3 \space Вт \cdot 3600 \space с = 6720 \cdot 10^6 \space Дж – 1321.2 \cdot 10^6 \space Дж = 5398.8 \cdot 10^6 \space Дж \approx 5400 \space МДж$.
Задача №6
Дано:
$\upsilon = 20 \frac<км><ч>$
$s = 100 \space км$
$m = 1 \space кг$
$\eta = 22 \% = 0.22$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$\upsilon \approx 5.6 \frac<м><с>$
$s = 100 \cdot 10^3 \space м$
Показать решение и ответ
Решение:
Мощность по определению:
$N = \frac
Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$\eta = \frac
Подставим в формулу для расчета КПД:
$\eta = \frac
Выразим отсюда полезную работу:
$A_п = \eta \cdot qm$.
Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = \frac<\upsilon>$.
Задача №7
Дано:
$N = 36.6 \space кВт$
$t = 1 \space ч$
$m = 10 \space кг$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 36.6 \cdot 10^3 \space Вт$
$t = 3600 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Задача №8
Дано:
$N = 220 \space кВт$
$t = 8 \space ч$
$\eta = 15 \% = 0.15$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 220 \cdot 10^3 \space Вт$
$t = 28.8 \cdot 10^3 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД:
$\eta = \frac
Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$\eta = \frac
Выразим отсюда массу каменного угля:
$m = \frac$.
Задача №9
Дано:
$Q_1 = 12.57 \space МДж$
$t = 1 \space ч$
$N = 735 \space Вт$
СИ:
$Q_1 = 12.57 \cdot 10^6 \space Дж$
$t = 3600 \space с$
Показать решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$\eta = \frac
$\eta = \frac<735 \space Вт \cdot 3600 с> <12.57 \cdot 10^6 \space Дж>\cdot 100 \% \approx 21 \%$.
Задача №10
Дано:
$N = 367 \space кВт$
$m = 60 \space т$
$\eta = 30 \% = 0.3$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$N = 367 \cdot 10^3 \space Вт$
$m = 60 \cdot 10^3 \space кг$
Показать решение и ответ
Решение:
Формула для расчета КПД теплового двигателя:
$\eta = \frac
Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$\eta = \frac
Выразим отсюда время, за которое была совершена полезная работа:
$t = \frac
КПД теплового двигателя
Содержание
В данном разделе вы уже познакомились с устройством и принципом работы двух видов теплового двигателя: двигателя внутреннего сгорания и паровой турбины. Используя эти механизмы, мы совершаем какую-то работу. Очевидно, что работа будет совершаться за счет энергии, которая выделяется при сгорании топлива. Но большая часть этой энергии теряется в окружающей среде. То есть, эта часть энергии не используется полезно.
Следовательно, и работу таких механизмов тогда нужно рассчитывать специальным образом. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. В данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.
Полезная работа теплового двигателя
Для того чтобы судить о полезной работе теплового двигателя, обратимся еще раз к его устройству. Если рассматривать его принцип работы, то устройство любого теплового двигателя можно представить в виде простой схемы (рисунок 1).
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника.
Рабочим телом является газ или пар. Например, в паровой турбине – это пар, в газовой – газ, в двигателе внутреннего сгорания – смесь паров бензина и воздуха.
Этот газ получает некоторое количество теплоты $Q_1$ от нагревателя. Под нагревателем подразумевается не какое-то специальное механическое устройство, как можно подумать. Нагреватель в схеме теплового двигателя – это горящее топливо.
Газ нагревается и расширяется. Так он совершает работу $A_п$, используя свою внутреннюю энергию.
Но важно понимать, что часть этой внутренней энергии $Q_2$ не совершает какую-то полезную для нас работу. Она передается вместе с отработанным паром или выхлопными газами атмосфере – холодильнику.
В качестве холодильника может использоваться резервуар с водой. Отработавший пар будет в таком случае приносить дополнительную пользу – нагревать воду для ее дальнейшего использования. Но этот процесс уже требует отдельного рассмотрения.
Итак, нас интересует именно та часть энергии топлива, выделяемая при его сгорании, которая превращается в полезную работу. От величины этой части энергии зависит экономичность двигателя.
Для этой характеристики мы вводим новое понятие – коэффициент полезного действия (КПД) теплового двигателя.
КПД теплового двигателя
Коэффициент полезного действия (КПД) теплового двигателя – это отношение совершенной полезной работы двигателя к энергии, полученной от нагревателя.
КПД теплового двигателя также как и КПД простейших механизмов, изученных вами в прошлом курсе, обозначается греческой буквой “эта” – $\eta$ и выражается в процентах.
Формула для расчета КПД теплового двигателя имеет следующий вид:
Средние значения КПД различных тепловых двигателей
В таблице 1 представлены средние значения КПД некоторых двигателей.
| Двигатель | КПД, % |
| Паровой двигатель | 8 |
| Двигатель внутреннего сгорания | 18 – 40 |
| Газовая турбина | 25 – 30 |
| Паровая турбина | 40 |
| Дизельный двигатель | 40 – 44 |
| Реактивный двигатель на жидком топливе | 47 |
Таблица 1. КПД различных двигателей
Одной из важнейших технических задач при проектировании двигателей является повышение значения КПД.
Примеры задач
Дано:
$\eta = 30 \%$
$Q_1 = 600 \space кДж$
СИ:
$6 \cdot 10^5 \space Дж$
Посмотреть решение и ответ
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac
Чтобы использовать эту формулу необходимо значение КПД, выраженное в процентах перевести в дробь:
$\eta = 30 \% = 0.3$
Дано:
$Q_1 = 155 \space Дж$
$Q_2 = 85 \space Дж$
Посмотреть решение и ответ
Решение:
Используем формулу для расчета КПД:
$\eta = \frac
Дано:
$A_п = 2.3 \cdot 10^4 \space кДж$
$m = 2 \space кг$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$2.3 \cdot 10^7 \space Дж$
Посмотреть решение и ответ
Решение:
В нашем случае нагревателем является бензин. Мы знаем его массу и удельную теплоту сгорания, поэтому можем рассчитать количество теплоты, выделенное при его сгорании по формуле:
$Q = Q_1 = qm$.
$Q_1 = 2 \space кг \cdot 4.6 \cdot 10^7 \frac<Дж> <кг>= 9.2 \cdot 10^7 \space Дж$.