Кпд тепловой машины равен 30 процентов при сгорании топлива
Кпд тепловой машины равен 30 процентов при сгорании топлива
КПД тепловой машины равен 25%. Это означает, что при выделении энергии Q при сгорании топлива на совершение полезной работы не используется энергия, равная
КПД по определению — та часть теплоты, отнимаемой от нагревателя, которая преобразуется в работу. Следовательно, на совершение полезной работы используется 0,25Q. Значит, в совершении полезной работы не используется энергия Q − 0,25Q = 0,75Q.
Правильный ответ указан под номером 1.
КПД тепловой машины равен 25%. Это означает, что при выделении энергии Q при сгорании топлива на совершение полезной работы затрачивается энергия, равная
Это задание ещё не решено, приводим решение прототипа.
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
Коэффициент полезного действия определяется как отношение полезной работы к совершённой работе, другими словами, какой процент совершаемой работы идёт на осуществление тех действий, которые мы считаем полезной работой. Поскольку КПД тепловой машины равен 30%, на совершение полезной работы пойдёт 30% тепла.
Правильный ответ указан под номером 4.
Тепловая машина с Коэффициентом полезного действия в 30% — это очень качественная машина. Как правило, тепловые двигатели работают с КПД 5−15%.
Аналоги к заданию № 170: 1570 4244 5396 5813 6341 Все
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
Это задание ещё не решено, приводим решение прототипа.
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
Коэффициент полезного действия определяется как отношение полезной работы к совершённой работе, другими словами, какой процент совершаемой работы идёт на осуществление тех действий, которые мы считаем полезной работой. Поскольку КПД тепловой машины равен 30%, на совершение полезной работы пойдёт 30% тепла.
Правильный ответ указан под номером 4.
Тепловая машина с Коэффициентом полезного действия в 30% — это очень качественная машина. Как правило, тепловые двигатели работают с КПД 5−15%.
Аналоги к заданию № 170: 1570 4244 5396 5813 6341 Все
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы не используется энергия, равная
Это задание ещё не решено, приводим решение прототипа.
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
Коэффициент полезного действия определяется как отношение полезной работы к совершённой работе, другими словами, какой процент совершаемой работы идёт на осуществление тех действий, которые мы считаем полезной работой. Поскольку КПД тепловой машины равен 30%, на совершение полезной работы пойдёт 30% тепла.
Правильный ответ указан под номером 4.
Тепловая машина с Коэффициентом полезного действия в 30% — это очень качественная машина. Как правило, тепловые двигатели работают с КПД 5−15%.
Аналоги к заданию № 170: 1570 4244 5396 5813 6341 Все
КПД тепловой машины равен 25%. Это означает, что при выделении энергии Q при сгорании топлива на совершение полезной работы не используется энергия, равная
Это задание ещё не решено, приводим решение прототипа.
КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
Коэффициент полезного действия определяется как отношение полезной работы к совершённой работе, другими словами, какой процент совершаемой работы идёт на осуществление тех действий, которые мы считаем полезной работой. Поскольку КПД тепловой машины равен 30%, на совершение полезной работы пойдёт 30% тепла.
Правильный ответ указан под номером 4.
Тепловая машина с Коэффициентом полезного действия в 30% — это очень качественная машина. Как правило, тепловые двигатели работают с КПД 5−15%.
Аналоги к заданию № 170: 1570 4244 5396 5813 6341 Все
Решение задач на сгорание топлива
Содержание
Из предыдущих уроков вы усвоили такие темы, как “Удельная теплоемкость“, “Количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении“, “Сгорание топлива. Удельная теплота сгорания“. Теперь мы можем перейти к решению задач на сгорание топлива, но при этом вам понадобятся знания из перечисленных выше уроков.
Также при решении задач вам могут понадобиться определенные справочные материалы для разных веществ: значения удельной теплоемкости, удельной теплоты сгорания и плотности.
Формулы, которые мы будем использовать в этом уроке:
Задача №1
Дано:
$m = 300 \space г$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$m = 0.3 \space кг$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Подставим в формулу известные величины и рассчитаем количество теплоты:
$Q = 4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 0.3 \space кг = 1.38 \cdot 10^7 \space Дж = 13.8 \cdot 10^6 \space Дж = 13.8 \space МДж$.
Задача №2
Дано:
$q = 3.8 \frac<МДж><кг>$
$m = 3.2 \space г$
СИ:
$q = 3.8 \cdot 10^6 \frac<Дж><кг>$
$m = 3.2 \cdot 10^ <-3>\space кг$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Подставим в формулу известные величины и рассчитаем количество теплоты:
$Q = 3.8 \cdot 10^6 \frac<Дж> <кг>\cdot 3.2 \cdot 10^ <-3>\space кг = 12.16 \cdot 10^3 \space Дж \approx 12.16 \space кДж$.
Такое количество теплоты выделяется при каждом выстреле.
Задача №3
Какая масса древесного угля при сгорании дает столько же энергии, сколько выделяется при сгорании четырех литров бензина?
Дано:
$V_б = 4 \space л$
$\rho_б = 710 \frac<кг><м^3>$
$q_б = 4.6 \cdot 10^7 \frac<Дж><кг>$
$q_у = 3.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$V_б = 4 \cdot 10^ <-3>\space м^3$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделившегося при сгорании древесного угля:
$Q_у = q_у m_у$.
Формула для расчета количества теплоты, выделившегося при сгорании бензина:
$Q_б = q_б m_б$.
Подставим в формулу для расчета количеста теплоты, выделившегося при сгорании бензина:
$Q_б = q_б \rho_б V_б$.
Теперь приравняем эти две формулы для нахождения количества теплоты (для бензина и для древесного угля):
$q_у m_у = q_б \rho_б V_б$.
Выразим отсюда массу древесного угля:
$m_у = \frac
Задача №4
При записи условий задачи, обозначим все величины, связанные с водой, нижним индексом “в”, а со спиртом – “с”.
Дано:
$V_в = 2 \space л$
$m_с = 10 \space г$
$t_1 = 20 \degree C$
$\rho_в = 1000 \frac<кг><м^3>$
$c_в = 4200 \frac<Дж><кг \cdot \degree C>$
$q_с = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$ V_в = 2 \cdot 10^ <-3>\space м^3$
$m_с = 0.01 \space кг$
Показать решение и ответ
Решение:
Рассчитаем количество теплоты, которое выделится при сгорании указанной массы спирта:
$Q_с = q_с m_с$,
$Q_с = 2.7 \cdot 10^7 \frac<Дж> <кг>\cdot 0.01 \space кг = 2.7 \cdot 10^5 \space Дж$.
Формула для расчета количества теплоты, необходимого для нагревания воды:
$Q_в = c_в m_в (t_2 – t_1)$.
Масса воды нам неизвестна, поэтому выразим ее через плотность и объем:
$m_в = \rho_в V_в$.
Подставим в формулу:
$Q_в = c_в \rho_в V_в (t_2 – t_1)$.
Задача №5
Дано:
$Q = 78.2 \space МДж$
$m_1 = 2m_2$
$q_1 = 1.5 \cdot 10^7 \frac<Дж><кг>$
$q_2 = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$Q = 7.82 \cdot 10^7 \space Дж$
Показать решение и ответ
Решение:
При сгорании бурого угля, содержащегося в смеси, выделилось количество теплоты:
$Q_1 = q_1 m_1$.
При сгорании каменного угля, содержащегося в смеси, выделилось количество теплоты:
$Q_2 = q_2 m_2$.
Выразим массу каменного угля через массу бурого и подставим в формулу:
$m_2 = \frac
$Q = q_1 m_1 + \frac
Выразим отсюда искомую массу бурого угля:
$Q = m_1 \cdot (q_1 + \frac
$m_1 = \frac
Задача №6
При записи условий задачи, обозначим все величины, связанные с водой, нижним индексом “в”, а с природным газом – “г”.
Дано:
$V_в = 10 \space л$
$\rho_в = 1000 \frac<кг><м^3>$
$t_1 = 10 \degree C$
$t_2 = 100 \degree C$
$c_в = 4200 \frac<Дж><кг \cdot \degree>$
$q_г = 4.4 \cdot 10^7 \frac<Дж><кг>$
$\rho_г = 0.8 \frac<кг><м^3>$
$r = 60 \%$
СИ:
$V_в = 10^ <-2>\space м^3$
Показать решение и ответ
Решение:
Выразим массу воды через ее плотность и объем:
$m_в = \rho_в V_в$.
Подставим ее в формулу и рассчитаем количество теплоты:
$Q_в = c_в \rho_в V_в (t_2 – t_1)$,
$Q_в = 4200 \frac<Дж> <кг \cdot \degree>\cdot 1000 \frac<кг> <м^3>\cdot 10^ <-2>\space м^3 \cdot (100 \degree C – 10 \degree C) = 42 \space 000 \frac<Дж> <\degree C>\cdot 90 \degree C = 3.78 \cdot 10^6 \space Дж$.
Количество теплоты, выделяемой при сгорании природного газа, вычисляется по формуле:
$Q_г = q_г m_г$.
Выразим массу через плотность и объем и подставим в эту формулу:
$m_г = \rho_г V_г$,
$Q_г = q_г \rho_г V_г$.
Подставим сюда выражение для количества теплоты, выделяемого при сгорании природного газа:
$q_г \rho_г V_г \cdot 60 \% = Q_в$.
Выразим отсюда объем природного газа:
$V_г = \frac
Задача №7
Для того чтобы записать условия задачи, давайте получим нужную нам информацию из представленных графиков.
Для того чтобы определить вид топлива, нам нужно найти его удельную теплоту сгорания. Значит, их мы и будем искать для ответа на первый вопрос задачи. Теперь можно записать условия задачи.
Дано:
$Q_1 = 150 \space МДж$
$Q_2 = 50 \space МДж$
$m_1 = 5 \space кг$
$m_2 = 3.5 \space кг$
$m = 2.2 \space кг$
СИ:
$Q_1 = 15 \cdot 10^7 \space Дж$
$Q_2 = 5 \cdot 10^7 \space Дж$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Выразим отсюда удельную теплоту сгорания:
$q = \frac
Найдем удельную теплоту сгорания для топлива, соответствующего графику №1:
$q_1 = \frac
Пользуясь таблицей из урока “Энергия топлива. Удельная теплота сгорания”, определяем, что такая величина удельной теплоты сгорания соответствует антрациту.
Найдем удельную теплоту сгорания для топлива, соответствующего графику №2:
$q_2 = \frac
Такая величина удельной теплоты сгорания соответствует торфу.
Задача №8
Дано:
$V_в = 4 \space л$
$m_к = 50 \space г$
$t_1 = 20 \degree C$
$t_2 = 75 \degree C$
$c_в = 4200 \frac<Дж><кг \cdot \degree C>$
$\rho_в = 1000 \frac<кг><м^3>$
$q_к = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$V_в = 4 \cdot 10^ <-3>м^3$
$m_к = 0.05 \space кг$
Показать решение и ответ
Решение:
КПД определяется по формуле:
$\eta = \frac
В нашем случае полезное количество теплоты – это количество теплоты, которое требуется для нагревании воды, а затраченное количество теплоты – это та энергия, которая выделялась при сгорании керосина.
Тогда формула для КПД примет вид:
$\eta = \frac
Теперь рассчитаем количество теплоты, которое выделится при сгорании керосина:
$Q_к = q_к m_к$,
$Q_к = 4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 0.05 \space кг = 0.23 \cdot 10^7 \space Дж$.
Подставим найденные значения в формулу для расчета КПД:
$\eta = \frac<0.0924 \cdot 10^7 \space Дж> <0.23 \cdot 10^7 \space Дж>\cdot 100\% \approx 0.402 \cdot 100 \% \approx 40.2 \%$.
Задача №9
Дано:
$\eta = 60 \% = 0.6$
$m_ч = 10 \space 000 \space кг$
$c_ч = 540 \frac<Дж><кг \cdot \degree C>$
$t_1 = 20 \degree C$
$t_2 = 1100 \degree C$
$q_у = 3.4 \cdot 10^7 \frac<Дж><кг>$
Показать решение и ответ
Решение:
Количество тепла, которое выделится при сгорании древесного угля, определяется по формуле:
$Q_у = q_у m_у$.
Выразим отсюда массу древесного угля:
$m_у = \frac
Рассчитаем его:
$Q_ч = 540 \frac<Дж> <кг \cdot \degree C>\cdot 10 \space 000 \space кг \cdot (1100 \degree C – 20 \degree C) = 0.54 \cdot 10^7 \frac<Дж> <кг>\cdot 1080 \degree C = 583.2 \cdot 10^7 \space Дж$.
Теперь мы можем рассчитать необходимую массу древесного угля:
$m_у = \frac<583.2 \cdot 10^7 \space Дж><0.6 \cdot 3.4 \cdot 10^7 \frac<Дж><кг>> = \frac<583.2 \space кг> <2.04>\approx 286 \space кг$.
Задача №10
Дано:
$\upsilon_ <ср>= 80 \frac<км><ч>$
$s = 320 \space км$
$V = 20 \space л$
$\rho = 710 \frac<кг><м^3>$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
$\eta = \frac<1><3>$
СИ:
$\upsilon_ <ср>\approx 22.2 \frac<м>
$s = 320 \space 000 \space м$
$V = 20 \cdot 10^<-3 >\space м^3$
Показать решение и ответ
Решение:
По определению средняя мощность определяется следующим образом:
$N_ <ср>= \frac
Время мы моем определить, используя известные среднюю скорость и путь:
$t = \frac< \upsilon_<ср>>$.
Тогда полезная работа будет рассчитываться по формуле:
$A = Q \cdot \eta = q \rho V \cdot \eta$.
Рассчитаем ее:
$N_ <ср>= \frac<4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 710 \frac<кг> <м^3>\cdot 20 \cdot 10^ <-3>\space м^3 \cdot \frac<1> <3>\cdot 22.2 \frac<м><с>> <320 \space 000 м>\approx \frac<4834 \cdot 10^6> <0.32 \cdot 10^6>\cdot \frac<Дж> <с>\approx 15 \space 106 \space Вт \approx 15 \space кВт$.
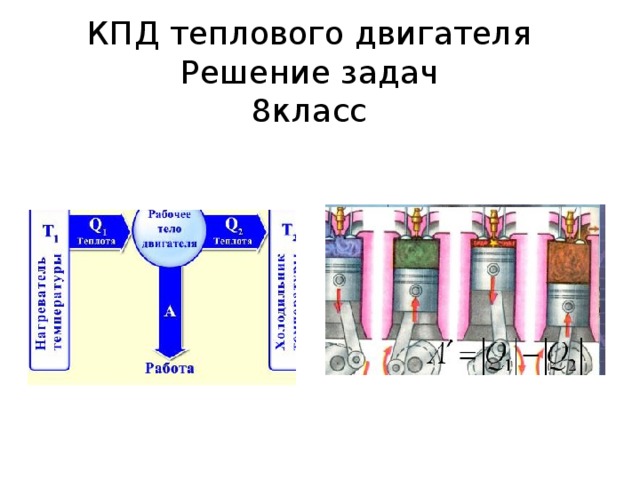
КПД теплового двигателя. Решение задач. 8класс
Данная презентация поможет при решениии задач по теме КПД в 8 классе
Просмотр содержимого документа
«КПД теплового двигателя. Решение задач. 8класс»
КПД теплового двигателя Решение задач 8класс
1. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 230 кДж, а отдает холодильнику количество теплоты, равное 100 кДж. Определите полезную работу двигателя за это время.
2. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 120кДж, и совершает при этом полезную работу 20 кДж. Определите КПД такого двигателя.
3. КПД теплового двигателя равен 45%. Какую полезную работу совершит двигатель, если он получит от нагревателя количество теплоты, равное 600 кДж?
4. Количество теплоты, полученное от нагревателя тепловым двигателем, равно 10 кДж. За тоже время он отдает холодильнику количество теплоты, равное 5 кДж. Найдите работу, совершенную двигателем, и КПД этого двигателя.
5. На древесном угле массой 17г нагревают воду. Взяли 200г воды и нагрели от 15 0 С до 57 0 С. Найти КПД тепловой установки.
продолжение на следующем слайде

КПД теплового двигателя. Решение задач. 8класс
Данная презентация поможет при решениии задач по теме КПД в 8 классе
Просмотр содержимого документа
«КПД теплового двигателя. Решение задач. 8класс»
КПД теплового двигателя Решение задач 8класс
1. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 230 кДж, а отдает холодильнику количество теплоты, равное 100 кДж. Определите полезную работу двигателя за это время.
2. Тепловой двигатель за некоторое время получает от нагревателя количество теплоты, равное 120кДж, и совершает при этом полезную работу 20 кДж. Определите КПД такого двигателя.
3. КПД теплового двигателя равен 45%. Какую полезную работу совершит двигатель, если он получит от нагревателя количество теплоты, равное 600 кДж?
4. Количество теплоты, полученное от нагревателя тепловым двигателем, равно 10 кДж. За тоже время он отдает холодильнику количество теплоты, равное 5 кДж. Найдите работу, совершенную двигателем, и КПД этого двигателя.
5. На древесном угле массой 17г нагревают воду. Взяли 200г воды и нагрели от 15 0 С до 57 0 С. Найти КПД тепловой установки.
продолжение на следующем слайде

Решение задач на сгорание топлива
Содержание
Из предыдущих уроков вы усвоили такие темы, как “Удельная теплоемкость“, “Количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении“, “Сгорание топлива. Удельная теплота сгорания“. Теперь мы можем перейти к решению задач на сгорание топлива, но при этом вам понадобятся знания из перечисленных выше уроков.
Также при решении задач вам могут понадобиться определенные справочные материалы для разных веществ: значения удельной теплоемкости, удельной теплоты сгорания и плотности.
Формулы, которые мы будем использовать в этом уроке:
Задача №1
Дано:
$m = 300 \space г$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$m = 0.3 \space кг$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Подставим в формулу известные величины и рассчитаем количество теплоты:
$Q = 4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 0.3 \space кг = 1.38 \cdot 10^7 \space Дж = 13.8 \cdot 10^6 \space Дж = 13.8 \space МДж$.
Задача №2
Дано:
$q = 3.8 \frac<МДж><кг>$
$m = 3.2 \space г$
СИ:
$q = 3.8 \cdot 10^6 \frac<Дж><кг>$
$m = 3.2 \cdot 10^ <-3>\space кг$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Подставим в формулу известные величины и рассчитаем количество теплоты:
$Q = 3.8 \cdot 10^6 \frac<Дж> <кг>\cdot 3.2 \cdot 10^ <-3>\space кг = 12.16 \cdot 10^3 \space Дж \approx 12.16 \space кДж$.
Такое количество теплоты выделяется при каждом выстреле.
Задача №3
Какая масса древесного угля при сгорании дает столько же энергии, сколько выделяется при сгорании четырех литров бензина?
Дано:
$V_б = 4 \space л$
$\rho_б = 710 \frac<кг><м^3>$
$q_б = 4.6 \cdot 10^7 \frac<Дж><кг>$
$q_у = 3.4 \cdot 10^7 \frac<Дж><кг>$
СИ:
$V_б = 4 \cdot 10^ <-3>\space м^3$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделившегося при сгорании древесного угля:
$Q_у = q_у m_у$.
Формула для расчета количества теплоты, выделившегося при сгорании бензина:
$Q_б = q_б m_б$.
Подставим в формулу для расчета количеста теплоты, выделившегося при сгорании бензина:
$Q_б = q_б \rho_б V_б$.
Теперь приравняем эти две формулы для нахождения количества теплоты (для бензина и для древесного угля):
$q_у m_у = q_б \rho_б V_б$.
Выразим отсюда массу древесного угля:
$m_у = \frac
Задача №4
При записи условий задачи, обозначим все величины, связанные с водой, нижним индексом “в”, а со спиртом – “с”.
Дано:
$V_в = 2 \space л$
$m_с = 10 \space г$
$t_1 = 20 \degree C$
$\rho_в = 1000 \frac<кг><м^3>$
$c_в = 4200 \frac<Дж><кг \cdot \degree C>$
$q_с = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$ V_в = 2 \cdot 10^ <-3>\space м^3$
$m_с = 0.01 \space кг$
Показать решение и ответ
Решение:
Рассчитаем количество теплоты, которое выделится при сгорании указанной массы спирта:
$Q_с = q_с m_с$,
$Q_с = 2.7 \cdot 10^7 \frac<Дж> <кг>\cdot 0.01 \space кг = 2.7 \cdot 10^5 \space Дж$.
Формула для расчета количества теплоты, необходимого для нагревания воды:
$Q_в = c_в m_в (t_2 – t_1)$.
Масса воды нам неизвестна, поэтому выразим ее через плотность и объем:
$m_в = \rho_в V_в$.
Подставим в формулу:
$Q_в = c_в \rho_в V_в (t_2 – t_1)$.
Задача №5
Дано:
$Q = 78.2 \space МДж$
$m_1 = 2m_2$
$q_1 = 1.5 \cdot 10^7 \frac<Дж><кг>$
$q_2 = 2.7 \cdot 10^7 \frac<Дж><кг>$
СИ:
$Q = 7.82 \cdot 10^7 \space Дж$
Показать решение и ответ
Решение:
При сгорании бурого угля, содержащегося в смеси, выделилось количество теплоты:
$Q_1 = q_1 m_1$.
При сгорании каменного угля, содержащегося в смеси, выделилось количество теплоты:
$Q_2 = q_2 m_2$.
Выразим массу каменного угля через массу бурого и подставим в формулу:
$m_2 = \frac
$Q = q_1 m_1 + \frac
Выразим отсюда искомую массу бурого угля:
$Q = m_1 \cdot (q_1 + \frac
$m_1 = \frac
Задача №6
При записи условий задачи, обозначим все величины, связанные с водой, нижним индексом “в”, а с природным газом – “г”.
Дано:
$V_в = 10 \space л$
$\rho_в = 1000 \frac<кг><м^3>$
$t_1 = 10 \degree C$
$t_2 = 100 \degree C$
$c_в = 4200 \frac<Дж><кг \cdot \degree>$
$q_г = 4.4 \cdot 10^7 \frac<Дж><кг>$
$\rho_г = 0.8 \frac<кг><м^3>$
$r = 60 \%$
СИ:
$V_в = 10^ <-2>\space м^3$
Показать решение и ответ
Решение:
Выразим массу воды через ее плотность и объем:
$m_в = \rho_в V_в$.
Подставим ее в формулу и рассчитаем количество теплоты:
$Q_в = c_в \rho_в V_в (t_2 – t_1)$,
$Q_в = 4200 \frac<Дж> <кг \cdot \degree>\cdot 1000 \frac<кг> <м^3>\cdot 10^ <-2>\space м^3 \cdot (100 \degree C – 10 \degree C) = 42 \space 000 \frac<Дж> <\degree C>\cdot 90 \degree C = 3.78 \cdot 10^6 \space Дж$.
Количество теплоты, выделяемой при сгорании природного газа, вычисляется по формуле:
$Q_г = q_г m_г$.
Выразим массу через плотность и объем и подставим в эту формулу:
$m_г = \rho_г V_г$,
$Q_г = q_г \rho_г V_г$.
Подставим сюда выражение для количества теплоты, выделяемого при сгорании природного газа:
$q_г \rho_г V_г \cdot 60 \% = Q_в$.
Выразим отсюда объем природного газа:
$V_г = \frac
Задача №7
Для того чтобы записать условия задачи, давайте получим нужную нам информацию из представленных графиков.
Для того чтобы определить вид топлива, нам нужно найти его удельную теплоту сгорания. Значит, их мы и будем искать для ответа на первый вопрос задачи. Теперь можно записать условия задачи.
Дано:
$Q_1 = 150 \space МДж$
$Q_2 = 50 \space МДж$
$m_1 = 5 \space кг$
$m_2 = 3.5 \space кг$
$m = 2.2 \space кг$
СИ:
$Q_1 = 15 \cdot 10^7 \space Дж$
$Q_2 = 5 \cdot 10^7 \space Дж$
Показать решение и ответ
Решение:
Формула для расчета количества теплоты, выделяющегося при сгорании топлива:
$Q = qm$.
Выразим отсюда удельную теплоту сгорания:
$q = \frac
Найдем удельную теплоту сгорания для топлива, соответствующего графику №1:
$q_1 = \frac
Пользуясь таблицей из урока “Энергия топлива. Удельная теплота сгорания”, определяем, что такая величина удельной теплоты сгорания соответствует антрациту.
Найдем удельную теплоту сгорания для топлива, соответствующего графику №2:
$q_2 = \frac
Такая величина удельной теплоты сгорания соответствует торфу.
Задача №8
Дано:
$V_в = 4 \space л$
$m_к = 50 \space г$
$t_1 = 20 \degree C$
$t_2 = 75 \degree C$
$c_в = 4200 \frac<Дж><кг \cdot \degree C>$
$\rho_в = 1000 \frac<кг><м^3>$
$q_к = 4.6 \cdot 10^7 \frac<Дж><кг>$
СИ:
$V_в = 4 \cdot 10^ <-3>м^3$
$m_к = 0.05 \space кг$
Показать решение и ответ
Решение:
КПД определяется по формуле:
$\eta = \frac
В нашем случае полезное количество теплоты – это количество теплоты, которое требуется для нагревании воды, а затраченное количество теплоты – это та энергия, которая выделялась при сгорании керосина.
Тогда формула для КПД примет вид:
$\eta = \frac
Теперь рассчитаем количество теплоты, которое выделится при сгорании керосина:
$Q_к = q_к m_к$,
$Q_к = 4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 0.05 \space кг = 0.23 \cdot 10^7 \space Дж$.
Подставим найденные значения в формулу для расчета КПД:
$\eta = \frac<0.0924 \cdot 10^7 \space Дж> <0.23 \cdot 10^7 \space Дж>\cdot 100\% \approx 0.402 \cdot 100 \% \approx 40.2 \%$.
Задача №9
Дано:
$\eta = 60 \% = 0.6$
$m_ч = 10 \space 000 \space кг$
$c_ч = 540 \frac<Дж><кг \cdot \degree C>$
$t_1 = 20 \degree C$
$t_2 = 1100 \degree C$
$q_у = 3.4 \cdot 10^7 \frac<Дж><кг>$
Показать решение и ответ
Решение:
Количество тепла, которое выделится при сгорании древесного угля, определяется по формуле:
$Q_у = q_у m_у$.
Выразим отсюда массу древесного угля:
$m_у = \frac
Рассчитаем его:
$Q_ч = 540 \frac<Дж> <кг \cdot \degree C>\cdot 10 \space 000 \space кг \cdot (1100 \degree C – 20 \degree C) = 0.54 \cdot 10^7 \frac<Дж> <кг>\cdot 1080 \degree C = 583.2 \cdot 10^7 \space Дж$.
Теперь мы можем рассчитать необходимую массу древесного угля:
$m_у = \frac<583.2 \cdot 10^7 \space Дж><0.6 \cdot 3.4 \cdot 10^7 \frac<Дж><кг>> = \frac<583.2 \space кг> <2.04>\approx 286 \space кг$.
Задача №10
Дано:
$\upsilon_ <ср>= 80 \frac<км><ч>$
$s = 320 \space км$
$V = 20 \space л$
$\rho = 710 \frac<кг><м^3>$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$
$\eta = \frac<1><3>$
СИ:
$\upsilon_ <ср>\approx 22.2 \frac<м>
$s = 320 \space 000 \space м$
$V = 20 \cdot 10^<-3 >\space м^3$
Показать решение и ответ
Решение:
По определению средняя мощность определяется следующим образом:
$N_ <ср>= \frac
Время мы моем определить, используя известные среднюю скорость и путь:
$t = \frac< \upsilon_<ср>>$.
Тогда полезная работа будет рассчитываться по формуле:
$A = Q \cdot \eta = q \rho V \cdot \eta$.
Рассчитаем ее:
$N_ <ср>= \frac<4.6 \cdot 10^7 \frac<Дж> <кг>\cdot 710 \frac<кг> <м^3>\cdot 20 \cdot 10^ <-3>\space м^3 \cdot \frac<1> <3>\cdot 22.2 \frac<м><с>> <320 \space 000 м>\approx \frac<4834 \cdot 10^6> <0.32 \cdot 10^6>\cdot \frac<Дж> <с>\approx 15 \space 106 \space Вт \approx 15 \space кВт$.