Лабораторная работа проверка основного закона динамики поступательного движения на машине атвуда
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
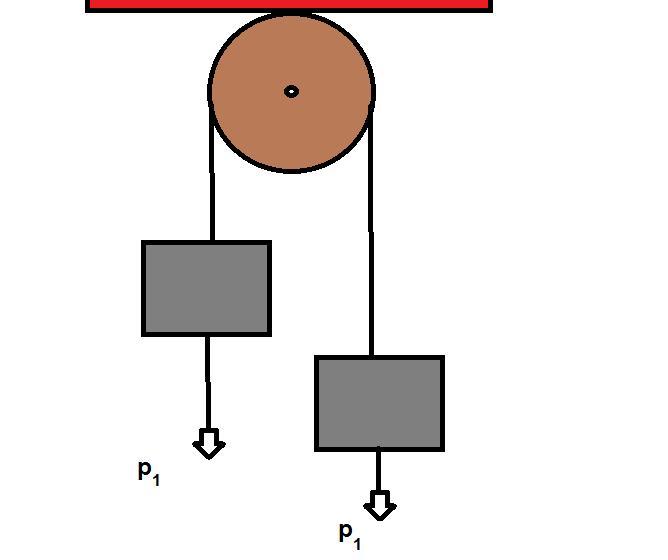
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Лабораторная работа: Изучение вращательного и поступательного движений на машине Атвуда
| Название: Изучение вращательного и поступательного движений на машине Атвуда Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 15:41:29 13 июня 2011 Похожие работы Просмотров: 949 Комментариев: 12 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
1 – стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн; 6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – регулировочная опора.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Случайная погрешность: 
Коэффициент Стьюдента: t = 2,1 (доверительная вероятность a=0,9
Среднеквадратичное отклонение: 
σ(t)сис – систематическая погрешность (погрешность измерительного прибора в данном случае милисекундомера). σ(t)сис = 1мс = 0,001с
Общая погрешность измерений: 
Расчет погрешности измерений t 2 : σ(t 2 )=2t σ(t) (3,4)
Момент инерции блока 
Масса блока m = Vp, где p-плотность латунного блока 8400кг/м 3 (3,6)


4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Измеренные значения и результаты их обработки приведены в таблице.
МУ 4586: Изучение динамики поступательного движения тела с помощью машины Атвуда
Лабораторная работа 1-16: Изучение динамики поступательного движения тела с помощью машины Атвуда
Цель работы: изучение динамики поступательного движения тела в поле сил земного тяготения, определение ускорения свободного паде- ния.
Приборы и принадлежности: машина Атвуда, блок электронный ФМ-1/1, набор грузов и перегрузков.
Элементы теории и метод эксперимента
Машина Атвуда используется для изучения законов динамики движения тел в поле земного тяготения. Она представляет собой на- стольный прибор, изображенный на рис. 1.
Принцип работы машины Атвуда заключается в следующем. Если на концах нити висят грузы A и B одинаковой массы M, то система должна находиться в положении безразличного равновесия. Когда на один из грузов (например, груз B) кладут перегрузок С массы m, то система выходит из положения равновесия и грузы А и B начинают двигаться равноускоренно. В комплект установки, помимо грузов, входит несколько перегрузков различной массы, что позволяет изучать движение с различными ускорениями.
Согласно второму закону Ньютона
где a – ускорение груза вместе с перегрузком.
На левый груз будут действовать две силы: Mg и
Так как блок невесом, то равен
Измеряя пройденный правым грузом путь S и время движения t, можно проверить равноускоренный характер движения груза:
Определение ускорения свободного падения, казалось бы, можно провести на основе формулы (4). Пусть аэ — экспериментальное ускоре- ние, вычисленное из (5). Подставляя аэ в (4), получаем
Однако вычисление g по формуле (6) и сопоставление его с таб- личным покажут, что вычисленное и табличное значения g плохо согла- суются друг с другом. Такое расхождение связано со следующими при- чинами.
Попробуем учесть теоретически, как эти величины видоизменяют соответствующие формулы для вычисления величин а и g, и опишем методику обработки полученных результатов в каждом опыте.
Для этого рассмотрим вращательное движение блока машины Атвуда. Основной закон динамики вращательного движения тела имеет вид
Сумма Mzi — сумма проекций на ось z всех моментов сил, действующих на вращающееся тело; e — его угловое ускорение; J — момент инерции тела.
Направим ось z вдоль оси вращения блока. При движении грузов
на блок действуют вращающий момент (T1 — T2 )r и момент силы трения –Mтр. Тогда уравнение (7) примет вид
где gэ — экспериментальное значение ускорения свободного падения.
Формула (16) может служить основой для экспериментального оп- ределения ускорения свободного падения.
Подготовка установки к работе
Порядок выполнения работы
Для каждого из перегрузков mi, входящих в комплект лаборатор- ной установки, проведите серии опытов в указанном порядке.
8. Повторите пп. 3 – 7 ещё два раза.
9. Повторите пп. 1 – 8 ещё два раза для различных значений пути S.
Задание 1. Проверка равноускоренного характера движения перегрузков
Для каждого перегрузка miпостройте график зависимости S от
Ошибки измерений часто приводят к тому, что экспериментальные точки данной зависимости не лежат на одной прямой. Поэтому через точки следует провести «наилучшую прямую», т. е. прямую, проходящую на наименьшем расстоянии от большинства точек.
Задание 2. Определение ускорения свободного падения
Вопросы и задания для самоконтроля
Библиографический список
Изучение динамики поступательного движения тела с помощью машины Атвуда / Рязан. гос. радиотехн. ун-т; cост.: М.А. Буробин. Рязань, 2012. 8 с.
Содержат основные теоретические сведения, порядок выполнения работы и итоговые контрольные вопросы.
Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 2. Библиогр.: 3 назв.
Машина Атвуда, ускорение, равноускоренное движение, ускорение свободного падения
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Изучение динамики поступательного движения тела с помощью машины Атвуда
Составитель: Б у р о б и н Михаил Анатольевич
Редактор Р.К. Мангутова Корректор С.В. Макушина
Подписано в печать 20.04.12. Формат бумаги 60 × 84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
Лабораторная работа №5. Изучение законов кинематики и динамики поступательного движения с помощью машины Атвуда
Изучение законов кинематики и динамики поступательного движения с помощью машины Атвуда
Цель работы: изучение законов равноускоренного движения
Приборы и принадлежности: установка лабораторная «Машина Атвуда ФМ 11», набор грузов и разновесков
Ход работы
Задание 1. Определение ускорения из закона пути для равноускоренного движения и ускорения свободного падения.
Рисунок 1. Машина Атвуда
1. Перекинуть через блок 2 нить с двумя грузами 3 и 4 и убедиться, что система находится в положении безразличного равновесия.
2. Установить кронштейн с фотодатчиком 6 в нижней части шкалы вертикальной стойки, а фотодатчик расположить таким образом, чтобы правый груз при движение вниз проходил в центре рабочего окна фотодатчика (за нижнее положение груза берется риска шкалы, соответствующая риске на корпусе фотодатчика и являющаяся как бы продолжением оптической оси фотодатчика, которую пересекает движущийся груз). Установить правый груз в крайнем верхнем положении.
3. Положить на правый груз один из перегрузков 5. Нажать на кнопку «Пуск» блока. Происходит растормаживание электромагнита, правый груз начинает опускаться, и таймер блока начинает отсчет времени. При пересечении правым грузом оптической оси фотодатчика отсчет времени прекратится. Записать показания таймера, т.е. время движения грузов.
4. Определить по шкале пройденный грузом путь, как расстояние от нижней плоскости груза (в верхнем положении) до оптической оси фотодатчика.
5. Зная пройденный путь и время движения, определяем значение ускорения по формуле:
где S – путь, пройденный каждым грузом;
t – время движения грузов
6. Повторить измерения 3-4 раза, изменяя высоту подъема груза в верхнем положении. Найти среднее значение ускорение грузов.
7. Повторить измерения по пп. 2 – 6 с другим перегрузком.
8. Определить ускорение свободного падения по формуле:
Таблица 1
| № м /с 2 | |||||||||||
| 1 | 0,0048 | 0,06047 | 0,40 | 1,51 | 1,47 | 1,39 | 1,46 | 0,38 | 0,35 | 9,17 | 9,63 |
| 2 | 0,32 | 1,44 | 1,47 | 1,30 | 1,40 | 0,33 | |||||
| 3 | 0,22 | 1,24 | 1,14 | 1,08 | 1,15 | 0,33 | |||||
| 1 | 0,0101 | 0,06047 | 0,40 | 0,98 | 0,99 | 0,94 | 0,97 | 0,82 | 0,74 | 9,61 | |
| 2 | 0,32 | 0,85 | 0,81 | 0,86 | 0,84 | 0,76 | |||||
| 3 | 0,22 | 0,77 | 0,67 | 0,60 | 0,68 | 0,64 | |||||
| 1 | 0,0127 | 0,06047 | 0,40 | 0,82 | 0,83 | 0,81 | 0,82 | 0,98 | 0,93 | 9,83 | |
| 2 | 0,32 | 0,65 | 0,67 | 0,72 | 0,68 | 0,94 | |||||
| 3 | 0,22 | 0,48 | 0,55 | 0,50 | 0,51 | 0,87 |
9. Определяем относительную погрешность ускорения по формуле:
где


10. Вычислим ускорение свободного падения для широты Петербург, по формуле:

Задание 2. Проверка второго закона динамики.
Запишем общее аналитическое выражение закона в проекциях на ось OY:
где Fiy – сумма проекций всех сил на выбранную ось,
Mi – суммарная система грузов
Проверку 2-го закона динамики проводим в два этапа
1-й этап.
Убеждаемся в справедливости ay Fiy, при Mi const
с
 ,
,м /с 2
Убеждаемся в справедливости 
при неизменной движущей силе F.
Измерения проводим для двух случаев.
1-й случай. Все перегрузки находятся на грузе А. Находим ускорение системы так же, как делали это на 1-м этапе.
2-й случай. Добавляем по одинаковому перегрузку m1 на груз А и на груз В. В результате масса системы увеличится на 2m1, а отношение будет иметь вид
где M=MА=MВ,
m – первоначальная суммарная масса перегрузков на грузе А,