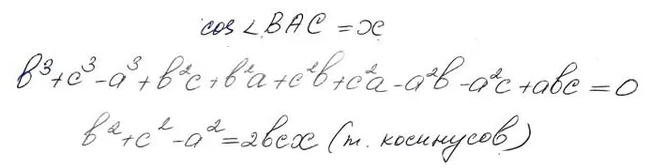Машина паскаля дата где и кем создано
ЭВМ: ЧТО? ГДЕ? КОГДА? | Суммирующая машина Паскаля
Паскалина (суммирующая машина Паскаля) — механическая счётная машина, изобретённая гениальный французским учёным Блезом Паскалем (1623—1662) в 1642 году.
Паскаль стал первым изобретателем механических счётных машин. Блез начал работу над машиной в возрасте 19 лет, наблюдая за работой своего отца, который был сборщиком налогов и часто выполнял долгие и утомительные расчёты.
Для своего времени Паскалина имела, конечно, довольно футуристический вид: механический «ящичек» с кучей шестерёнок. За десять лет Паскалю удалось собрать более 50 различных вариантов устройства. Складываемые числа вводились в машину при помощи поворотов наборных колёсиков, на каждое из которых были нанесены деления от 0 до 9, т.к. одно колёсико соответствовало одному десятичному разряду числа. Тем самым, чтобы ввести число, колесики прокручивались до соответствующей цифры. При совершении полного оборота, избыток над цифрой 9 колёсико переносило на соседний разряд, сдвигая рядом расположенное колесо на 1 позицию.
Первые экземпляры машины Паскаля имели пять зубчатых колёс, спустя время их число увеличилось до шести, а ещё чуть позже до восьми, что позволяло работать с многоразрядными числами, вплоть до 9 999 999. Ответ арифметических операций был виден в верхней части металлического корпуса устройства. Вращение колёс было возможно только в одном направлении, тем самым, исключая возможность работать с отрицательными числами. Примечательно, что машина Паскаля умела выполнять как сложение, так и другие операции, однако требовала при этом применения довольно неудобной процедуры повторных сложений. Вычитание выполнялось дополнениями до девятки, которые в качестве помощи считавшему появлялись в окошке, расположенном над выставленным оригинальным значением.
Преимущества автоматических вычислений никак не изменили ситуацию, т.к. использование десятичной машины для финансовых расчётов в рамках действовавшей во Франции до 1799 года денежной системы было занятием не из простых. Расчёты проводились в ливрах, су и денье. В «ливре» насчитывалось 20 «су», в то время как в «су» — 12 «денье». Похожая система была и в Великобритании. В результате использование десятичной системы счисления в недесятичных финансовых расчётах усложняло и без того трудный процесс вычислений.
Несмотря на вызываемый Паскалиной огромный восторг, машина не озолотила своего создателя. Техническая сложность и высокая стоимость машины в сочетании с небольшими даже для тех лет вычислительными способностями служили серьёзным барьером для её широкого распространения. И всё же, Машина Паскаля заслуженно вошла в историю, ведь заложенный в её основу принцип связанных колёс почти на 300 лет стал основой для большинства создаваемых вычислительных машин.
ЭВМ: ЧТО? ГДЕ? КОГДА? | Суммирующая машина Паскаля
Счетная суммирующая машина Блеза Паскаля – это изобретение, удивившее современников, но так и не нашедшее свой круг клиентов. Механизм, в основе имеющий зубчатые колесики, считается одним из прародителей калькулятора.
«Паскалина»: история возникновения
Создание одной из самых ранних моделей суммирующих машин принадлежит французскому физику и математику Блезу Паскалю. Отец Паскаля был сборщиком налогов, поэтому уже в 19 лет будущий ученый видел, как производятся разные счетные операции. Уже в этот период создаются первые чертежи «Паскалины». Всего на окончательную разработку аппарата ушло 5 лет.
В теории механизм Паскаля был достаточно прост в применении, но из-за слабого развития технической стороны осуществление плана ученого стало сложной задачей, для которой пришлось преодолеть множество трудностей.
Блез хотел, чтобы его суммирующая машина упростила произведение любых сложных расчетов, как человеку образованному, так и тому, кто мало что понимал в арифметике. Паскаль затронул важную проблему, касающуюся не только его семьи, а и развития науки ХVII века.
На протяжении 10 лет исследователь создал более 50 счетных машин, однако лишь малую долю своих изобретений он смог продать. Один из первых готовых аппаратов Паскаль отдал канцлеру Сергье как благодарность за его помощь в научной деятельности молодого Блеза.
Что такое счетная машина Блеза Паскаля?
Использование оборотов колеса для процесса сложения не был новшеством в научной деятельности Паскаля, так как эту идею озвучил еще в 1623 году Вильгельм Шиккард. А действительно изобретением Блеза считается перенос остатка в следующий разряд при полном вращении шестеренки.
В первых «паскалинах» было по пять зубчатых колесиков, а уже с дальнейшей модернизацией технологии в механизме их число доходило до восьми штук, что позволяло работать с большими числами (до 9999999).
Этот механизм активно использовался в разных технических приборах до ХХ века. Его преимуществом было умение автоматического складывания многозначных чисел самим прибором.
Исследователи истории возникновения счетных механизмов считают, что Паскаль создал свою суммирующую машину практически с нуля, так как не был ознакомлен с проектом Шиккарда.
Прибор удивил современную науку, однако из-за высокой стоимости и сложности в эксплуатации так и не смог обрести свою аудиторию. Все же изобретение Паскаля внесло огромный вклад в историю развития вычислительной техники.
Суммирующая машина Паскаля
Суммирующая машина Паскаля — арифметическая машина, изобретённая французским учёным Блезом Паскалем.
История
Француз Блез Паскаль начал создавать суммирующую машину «Паскалину» в 1642 году в возрасте 19 лет, наблюдая за работой своего отца, который был сборщиком налогов и часто выполнял долгие и утомительные расчёты.
Машина Паскаля представляла собой механическое устройство в виде ящичка с многочисленными связанными одна с другой шестерёнками. Складываемые числа вводились в машину при помощи соответствующего поворота наборных колёсиков. На каждое из этих колёсиков, соответствовавших одному десятичному разряду числа, были нанесены деления от 0 до 9. При вводе числа, колесики прокручивались до соответствующей цифры. Совершив полный оборот, избыток над цифрой 9 колёсико переносило на соседний разряд, сдвигая соседнее колесо на 1 позицию. Первые варианты «Паскалины» имели пять зубчатых колёс, позднее их число увеличилось до шести или даже восьми, что позволяло работать с большими числами, вплоть до 9999999. Ответ появлялся в верхней части металлического корпуса. Вращение колёс было возможно лишь в одном направлении, исключая возможность непосредственного оперирования отрицательными числами. Тем не менее, машина Паскаля позволяла выполнять не только сложение, но и другие операции, но требовала при этом применения довольно неудобной процедуры повторных сложений. Вычитание выполнялось при помощи дополнений до девятки, которые для помощи считавшему появлялись в окошке, размещённом над выставленным оригинальным значением.
Несмотря на преимущества автоматических вычислений использование десятичной машины для финансовых расчётов в рамках действовавшей в то время во Франции денежной системы было затруднительным. Расчёты велись в ливрах, су и денье. В ливре насчитывалось 20 су, в су — 12 денье. Использование десятичной системы в не десятичных финансовых расчётах усложняло и без того нелёгкий процесс вычислений.
Тем не менее, примерно за 10 лет Паскаль построил около 50 и даже сумел продать около дюжины вариантов своей машины. Несмотря на вызываемый ею всеобщий восторг, машина не принесла богатства своему создателю. Сложность и высокая стоимость машины в сочетании с небольшими вычислительными способностями служили препятствием её широкому распространению. Тем не менее, заложенный в основу «Паскалины» принцип связанных колёс почти на три столетия стал основой для большинства создаваемых вычислительных устройств.
Машина Паскаля стала вторым реально работающим вычислительным устройством после Считающих часов Вильгельма Шикарда (нем. Wilhelm Schickard ), созданных в 1623 году.
Переход Франции в 1799 году на метрическую систему коснулся также её денежной системы, которая стала, наконец, десятичной. Однако, практически до начала 19-го столетия создание и использование считающих машин оставалось невыгодным. Лишь в 1820 году Шарль Ксавье Тома де Кольмар запатентовал первый механический калькулятор, ставший коммерчески успешным.
Машина Паскаля со снятой крышкой
Механизация и машинизация вычислительных операция – одно из основополагающих технических достижений второй трети 20 века. Подобно тому, как появление первых прядильных машин послужило началом великого промышленного переворота 18-19 веков, создание электронной вычислительной машины стало предвестником грандиозной научно-технической и информационной революции второй половины 20-го. Этому важному событию предшествовала длинная предыстория. Первые попытки собрать счетную машину были еще в 17 веке, а простейшие вычислительные приспособления, типа абака и счет, появились еще раньше – в древности и средневековье.
Хотя автоматическое вычислительное устройство относится к роду машин, его нельзя поставить в один ряд с промышленными машинами, скажем, с токарным или ткацким станком, ведь в отличие от них оно оперирует не с физическим материалом (нитями или деревянными заготовками), а с идеальными, несуществующими в природе числами. Поэтому перед создателем любой вычислительной машины (будь то простейший арифмометр или новейший суперкомпьютер) стоят специфические проблемы, не возникающие у изобретателей в других областях техники. Их можно сформулировать следующим образом: 1) как физически (предметно) представить числа в машине? 2) как осуществить ввод исходных числовых данных? 3) каким образом смоделировать выполнение арифметических операций? 4) как представить вычислителю введенные исходные данные и результаты вычислений?
Что же представляла из себя эта первая в истории вычислительная машина и каким образом были разрешены перечисленные выше задачи? Механизм машины был заключен в легкий латунный ящичек. На верхней его крышке имелось 8 круглых отверстий, вокруг каждого из которых была нанесена круговая шкала. Шкала крайнего правого отверстия делилась на 12 равных частей, шкала соседнего с ним отверстия на 20 частей, остальные шесть отверстий имели десятичное деление. Такая градуировка соответствовала делению ливра – основной французской денежной единицы того времени: 1 су = 1/20 ливра и 1 денье = 1/12 су. В отверстиях были видны зубчатые установочное колеса, находившиеся ниже плоскости верхней крышки. Число зубьев каждого колеса было равно числу делений шкалы соответствующего отверстия.
Вычислительная машина Блеза Паскаля
Данная статья относится к Категории: ОРГ научной деятельности
«В 17 лет, желая помочь отцу в громоздких вычислительных операциях, связанных со сборам податей в Руанском генеральстве, интендантом которого был отец, Паскаль задумал создать счётную машину. Облегчение счёта путём его автоматизации было не только его личной задачей, а одной из актуальных научных проблем XVII столетия. […] Путь этот был тернистым, потребовавшим от Паскаля не только больших творческих усилий, но и огромного волевого и физического напряжения, а также значительных материальных затрат, на которые, кстати, не скупился его понимающий отец. […]
Созданию счётной машины Паскаль отдал 5 лет своей хрупкой и короткой жизни. Он вложил в неё все свои знания по математике, механике, физике, талант изобретателя, природную сноровку мастера. По замыслу Блеза, счётная машина-сумматор должна была облегчить сложные расчёты «без пера и жетона» любому человеку, не знакомому с математикой. В теоретическом плане принцип её действия довольно прост: автоматический перенос десятков с помощью вращательного движения зубчатых колес, замена десятков нулём в одном разряде и автоматическое прибавление единицы в следующем. Но для низкой техники того времени реализация этого простого замысла была сопряжена с невероятными трудностями, через которые пришлось пройти Паскалю.
Одну из первых готовых машин Паскаль с благодарственным посвящением подарил канцлеру Сегье, который в трудный момент поддержал пошатнувшиеся надежды юного изобретателя, «Кровавый палач» народа Сегье был покровителем наук и страстным собирателем редких книг и рукописей.
В 1649 г. канцлер добился от короля «Привилегии на арифметическую машину» для Паскаля, согласно которой за автором закреплялось право на приоритет, её изготовление и продажу. Некоторое время Паскаль занимался производством счётных машин и какое-то количество из них продал; посредником в деле сбыта машин был Роберваль, друг обоих Паскалей. Но кустарная техника того времени делала производство машины очень сложным и
дорогостоящим предприятием, которое не могло долго продержаться на личных средствах и героических усилиях изобретателя. Тем более что, тяжёлый труд на протяжении 5 лет подорвал и без того хрупкое здоровье Паскаля. Его начали мучить изнурительные головные боли, которые давали о себе знать всю последующую жизнь».
Стрельцова Г.Я., Паскаль и европейская культура, М., «Республика», 1994 г., с. 34-35.
Историки считают, что у Блеза Паскаля было до 50 вариантов счетной машины.
Изображения в статье
Счётная машина Паскаля, Автор: David.Monniaux, CC BY-SA 3.0
Механика проще, чем у часов. Просто Паскаль не умел делать часовые механизмы. Надо было часовому мастеру заказать шестеренки выточить. Ручной токарный станок появился еще когда.
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
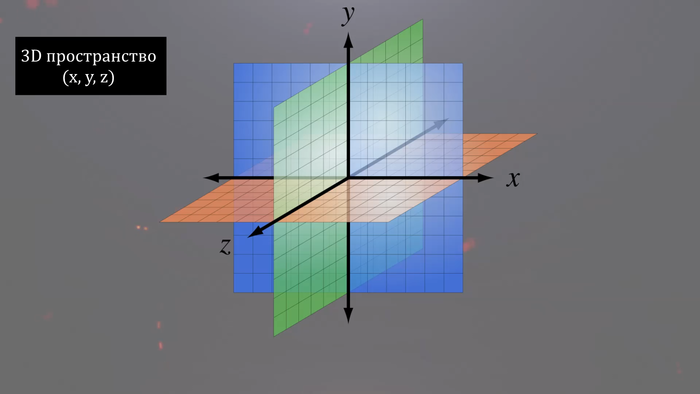
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
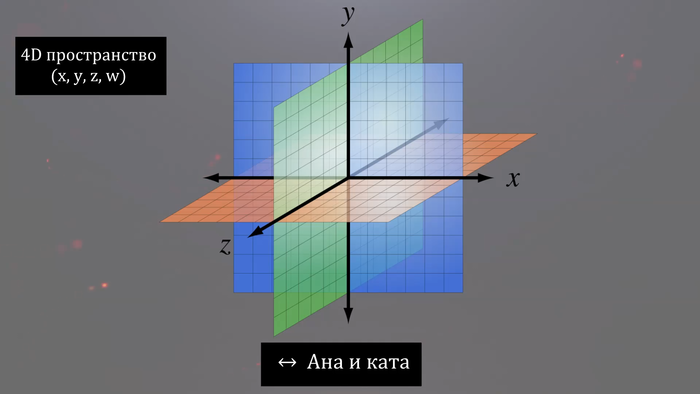
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
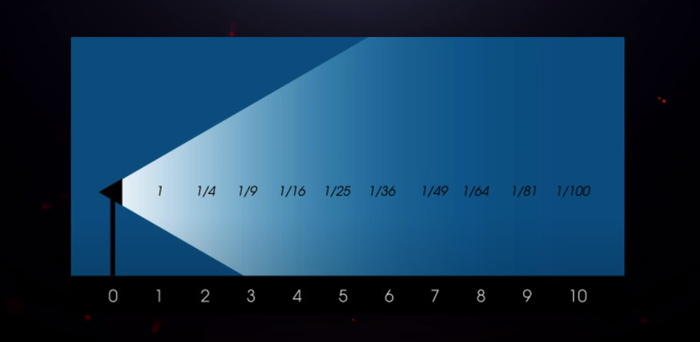
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
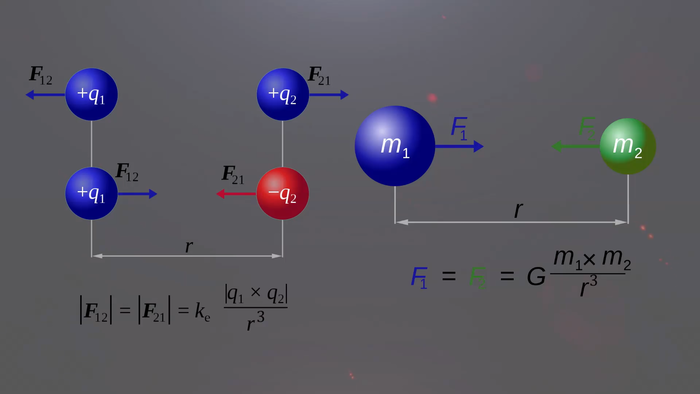
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
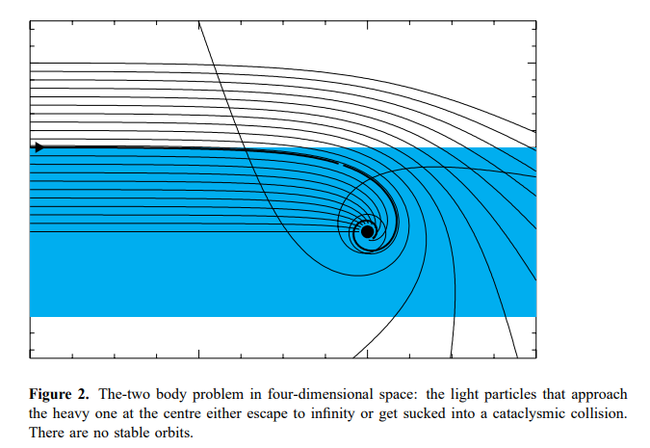
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
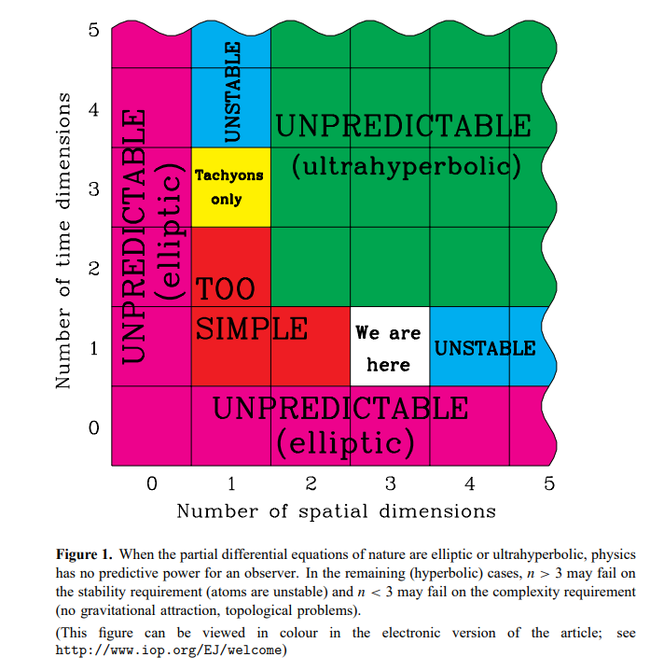
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году
Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.
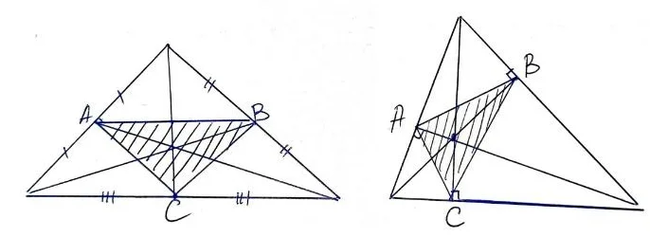
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?
Но, погодите, есть же еще биссектрисы!
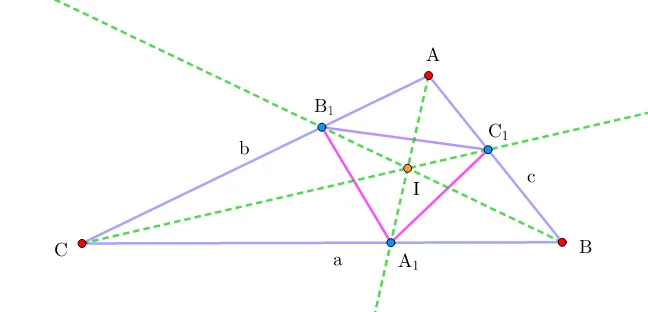
И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!
Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.
Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:
Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».
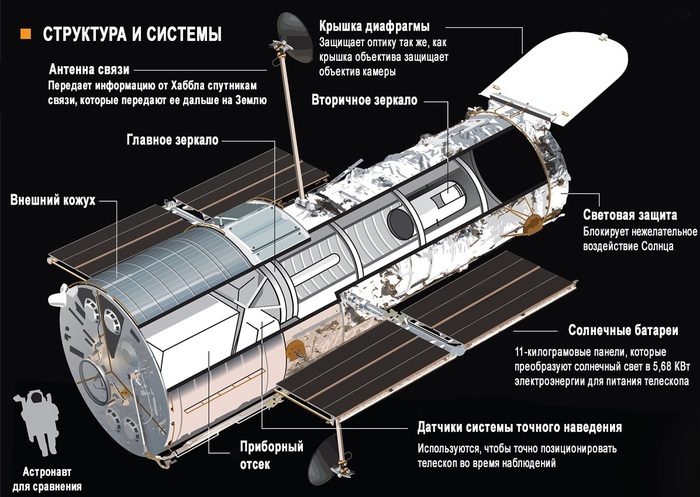
HUBBLE: космические неудачи
Космический телескоп «Хаббл» уже более 30 лет называют самым «зорким глазом» всех астрономов Земли. Не многие обсерватории могут похвастаться столь же мощным вкладом в науку.
Концепция орбитальной обсерватории зародилась ещё в 40х годах. Ученые поняли преимущества космического телескопа:
– На него не влияют погодные условия;
– На нем не отражаются атмосферные искажения;
– Он дает возможность вести наблюдение в инфракрасном и ультрафиолетовом спектрах.
Последний фактор особенно важен, так как именно в этих спектрах скрыто много ответов на фундаментальные вопросы науки. Земная атмосфера отражает большую часть излучения, поэтому астрономы не могли полноценно вести такие наблюдения.
Финансовая и техническая возможность доставить телескоп на орбиту появилась только спустя три десятилетия – подготовительные работы начались в 1978 году. Новый проект назвали в честь Эдвина Хаббла – ученого, подтвердившего существование других галактик и создавшего теорию о расширении Вселенной.
Хотелось бы сказать, что телескоп победоносно собрали и отправили, но… нет. Абсолютно все шло не по плану. NASA и ESA (Европейское Космическое Агентство) не вписались в изначальный бюджет более чем в 6 раз и провалили все сроки.
Подрядчики начали изготовление главного зеркала в 1979 году, но смогли завершить его только к концу 1981 года, неоднократно перенося дату окончания работ. И это только главное зеркало, а ведь оптики в телескопе предостаточно! Сотрудники NASA усомнились в компетентности специалистов этой фирмы, но потраченные миллионы не позволяли начать проект заново, с другой компанией.
Соответственно, неоднократно сдвигалась и дата запуска телескопа в космос.
В конечном итоге сотрудники NASA обозначили сроки как «неопределённые и изменяющиеся ежедневно».
Над созданием корпуса телескопа работала другая компания, но она также с треском провалилась, затянула работу на несколько месяцев и увеличила выделенные ей финансы на 30%.
Долгими стараниями телескоп был полностью готов (звук облегченного вздоха инвесторов). Запуск запланировали на октябрь 1986 года. Казалось бы, что может пойти не так?
Кроме катастрофы: крушение «Челленджера» в январе того же года унесло жизни 7 членов экипажа и на несколько лет свернуло программу «Спейс Шаттл». Именно эти шаттлы должны были доставить аппарат на орбиту. Хаббл был помещен в хранилище с искусственной атмосферой и защитой от коррозии. Каждый месяц хранения обходился NASA в 6 млн долларов.
Запуск был произведен только в апреле 1990 года, выкачав из NASA и ESA около 2,5 млрд долларов (при начальном бюджете в 400 млн долларов). А уже к 1999 году бюджет и вовсе превысил 6 млрд долларов.
«Ну теперь точно все будет хорошо!»
Все. кроме неверной формы главного зеркала. Да, именно того, которое усердно вытачивали больше двух лет. Первые же снимки, полученные с Хаббла, показали проблемы в резкости и отсутствие ожидаемого качества. Ученые провели сложнейшие расчеты и установили причину: зеркало было недостаточно сферическое по краям.
Только вдумайтесь! Отклонение от заданной формы всего на 2 микрона (в 40 раз меньше толщины волоса) чуть не поставило крест на всей космической программе. Техник, обслуживающий станок для изготовления зеркала, обнаружил зазор в линзе главного датчика-корректора и подложил под нее металлическую шайбу, чтобы линза не шаталась: «И так сойдет!»
Возвращать телескоп на Землю долго, дорого и опасно, а поменять зеркало в открытом космосе – невозможно. Несмотря на неправильную форму, зеркало было выточено и отполировано с высокой точностью, поэтому появилась возможность создать корректирующую систему: два дополнительных зеркала, которые компенсировали ошибку. Что-то вроде очков для гигантского телескопа. Установили их только спустя три года, во время первой экспедиции к телескопу Хаббл.
Друзья, спасибо, что прочитали мою статью. Надеюсь, она вам понравилась!
Математика
В Курчатовском институте запустили термоядерную установку впервые за последние 20 лет
Успех российской науки: первую за последние 20 лет термоядерную установку токамак Т-15МД, у которой нет аналогов в мире, запустили в Курчатовском институте в Москве⚡️
Псковский математик, разработавший способ моментально вычислять коррупционеров по декларациям, останется в СИЗО до суда
В Пскове один из районных судов постановил оставить в силе меру пресечения в виде заключения под стражу для местного математика Дмитрия Теплова. 57-летний мужчина был задержан после того, как представил в сети программно-математический алгоритм, позволяющий автоматически и с высокой долей вероятности вычислять чиновников по их налоговым декларациям.
Учёный утверждал, что психология среднестатистического коррупционера легко поддаётся изучению. Все они не умеют остановиться и стремятся украсть ещё больше и больше с каждым годом, причём как минимум часть подобных денег приходится отражать в декларациях, “легализовывая” их через бизнес, чтобы они хотя бы отдалённо соответствовали реальной картине и не вызывали подозрений. Рано или поздно каждый из них попадается на “очевидно нетрудовых сверхдоходах”, которые несложно описать математическими алгоритмами.
Теплов опубликовал в сети методы таких вычислений и продемонстрировал их высокую работоспособность – автоматизированный анализ деклараций уже осужденных коррупционеров давал результаты порядка 92-99%, причём аналогичная вероятность оказаться коррупционером была найдена у множества действующих чиновников. Вскоре исследователя задержали по обвинению в клевете на представителей органов власти и экстремизме.
Согласно очередному решению суда, учёный будет находиться под арестом, как подозреваемый, представляющий собой высокую опасность. В июне должен состояться суд, на котором будут рассмотрены обвинения против математика в разжигании ненависти к социальной группе “государственные служащие”, а также о клевете в отношении лиц из регионального и федерального правительств.
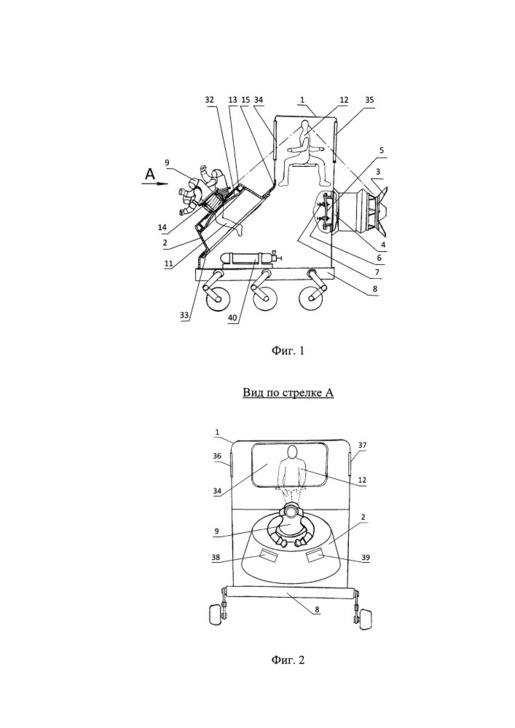
Ответ на пост «Роскосмос придумал гермокабину для работы на других планетах, а также под водой!»
В исходной новости говорится что РКК «Энергия» запатентовала устройство для выполнения ручных операций на поверхности других планет и в опасных газовых и жидких средах.
Предполагается что один из космонавтов наполовину находится в гермокабине, наполовину — во фрагменте скафандра, с помощью которого он выполняет внешние работы вручную.
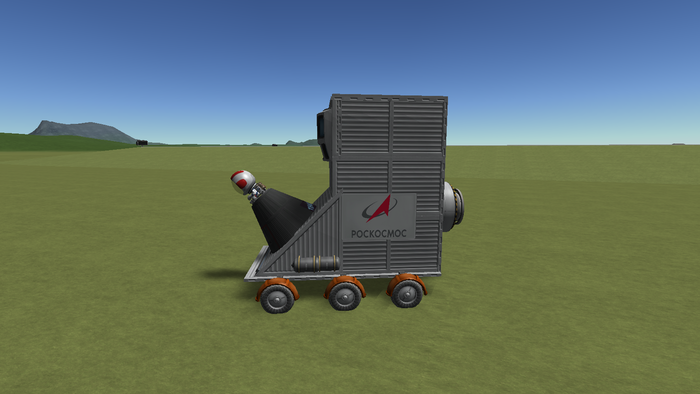
Так что желающие могут сравнить результаты и пофантазировать как это чудо могло бы выглядеть в готовом виде исходя из подобных вводных.
Хотя как по мне данному плоду греха Лунохода-2 и кентавра в этом контексте подходит слегка другое лого.
1) Как торчащий из шлюза космонавт вообще будет способен работать с чем либо за габаритами повозки не говоря уже о прямой работе с поверхностью небесного тела, находящейся метрах в трёх от него?
Обнаружена связь между аспирином и раком груди и мочевого пузыря
Миллионы людей по всем миру регулярно принимают аспирин. Новое исследование показало, что такое частое употребление снижает риск смерти от рака груди или мочевого пузыря на треть.
Аспирин разжижает кровь, тем самым снижая риск образования тромбов. Многие люди принимают его для профилактики сердечных заболеваний. Однако также считается, что препарат снижает риск развития рака кишечника. Авторы нового исследования доказали, что это справедливо и для некоторых других видов рака.
Результаты исследования основаны на изучении медицинских данных около 140 000 мужчин и женщин, участвовавших в скрининговом исследовании рака, которое длилось 13 лет. В основном все участники были старше 65 лет. В ходе исследования они также проходили анкитирование, в котором был вопрос об употреблении аспирина.
Ученые заметили связь между раком груди и мочевого пузыря и приемом аспирина. Люди, которые принимали его хотя бы три раза в неделю, имели меньше шансов умереть от рака (на четверть меньше для рака груди и на треть для рака мочевого пузыря). Более того, постоянное употребление (но не регулярное) уменьшало риск смерти от рака на 25% по сравнению с теми, кто никогда не пил аспирин.
Доктор Луманс-Кропп, один из авторов работы, сказал: «Прием аспирина три раза в неделю связан с сильным снижением риска, и любое его применение увеличивает шансы выжить при раке мочевого пузыря и молочной железы. Эти результаты указывают на то, что при лечении некоторых типов рака аспирин может быть полезным».
Дальнейшие эксперименты показали, что препарат помогает организму бороться с воспалительными процессами при раке молочной железы и мочевого пузыря. Однако авторы работы отмечают, что важно понимать, что аспирин не уменьшает риск развития заболевания, не лечит и не останавливает другие виды рака, препарат влияет именно на вероятность смертельного исхода.
Также ученые говорят, что по-прежнему необходимо учитывать вред от длительного использования аспирина, так как препарат может вызвать опасные желудочные кровотечения. Исследователи считают, что сейчас необходимо провести дополнительный ряд работ, чтобы пролить свет на потенциальные защитные эффекты аспирина.
Особая обувь для стариков
Особая обувь для стариков, с которой невозможно упасть. Она мгновенно улавливает сенсорами неверные шаги, балансируя и стабилизируя стойку «хозяина».
В 1936 году он создал вычислительную машину, все математические операции в которой выполняла текущая вода. Слышали ли вы о таком?
Первый гидроинтегратор ИГ-1 был предназначен для решения наиболее простых – одномерных задач. В 1941 году сконструирован двухмерный гидравлический интегратор в виде отдельных секций. В последствии интегратор был модифицирован для решения трехмерных задач.
После организации серийного производства интеграторы стали экспортироваться за границу: в Чехословакию, Польшу, Болгарию и Китай. Но самое большое распространение они получили в нашей стране. С их помощью провели научные исследования в поселке «Мирный», расчеты проекта Каракумского канала и Байкало-Амурской магистрали. Гидроинтеграторы успешно использовались в шахтостроении, геологии, строительной теплофизике, металлургии, ракетостроении и во многих других областях.
И еще немного для тех, кому интересны подробности.
Создание гидроинтегратора продиктовано сложной инженерной задачей, с которой молодой специалист В. Лукьянов столкнулся в первый же год работы.
После окончания Московского института инженеров путей сообщения (МИИТ) Лукьянов был направлен на постройку железных дорог Троицк-Орск и Карталы-Магнитная (ныне Магнитогорск).
Лукьянов заинтересовался причинами образования трещин в бетоне. Его предположение об их температурном происхождении сталкивается со скептическим отношением специалистов. Молодой инженер начинает исследования температурных режимов в бетонных кладках в зависимости от состава бетона, используемого цемента, технологии проведения работ и внешних условий. Распределение тепловых потоков описывается сложными соотношениями между температурой и меняющимися со временем свойствами бетона. Эти соотношения выражаются так называемыми уравнениями в частных производных. Однако существовавшие в то время (1928 год) методы расчетов не смогли дать быстрого и точного их решения.
Академик Николай Николаевич Павловский (1884-1937) занимался вопросами гидравлики. В 1918 году доказал возможность замены одного физического процесса другим, если они описываются одним и тем же уравнением (принцип аналогии при моделировании).
Главным его узлом стали вертикальные основные сосуды определенной емкости, соединенные между собой трубками с изменяемыми гидравлическими сопротивлениями и подключенные к подвижным сосудам. Поднимая и опуская их, меняли напор воды в основных сосудах. Пуск или остановка процесса расчета производились кранами с общим управлением.
Для решения задачи на гидроинтеграторе необходимо было:
1) составить расчетную схему исследуемого процесса;
2) на основании этой схемы произвести соединение сосудов, определить и подобрать величины гидравлических сопротивлений трубок;
3) рассчитать начальные значения искомой величины;
4) начертить график изменения внешних условий моделируемого процесса.
Возможности гидроинтегратора оказались необычайно широки и перспективны. В 1938 году В. С. Лукьяновым была основана лаборатория гидравлических аналогий, которая вскоре превратилась в базовую организацию для внедрения метода в народное хозяйство страны. Руководителем этой лаборатории он оставался в течение сорока лет.
В 1949 году постановлением Совета Министров СССР в Москве создан специальный институт «НИИСЧЕТМАШ», которому были получены отбор и подготовка к серийному производству новых образцов вычислительной техники. Одной из первых таких машин стал гидроинтегратор. За шесть лет в институте разработана новая его конструкция из стандартных унифицированных блоков, и на Рязанском заводе счетно-аналитических машин начался их серийный выпуск с заводской маркой ИГЛ (интегратор гидравлический системы Лукьянова). Ранее единичные гидравлические интеграторы строились на Московском заводе счетно-аналитических машин (САМ). В процессе производства секции были модифицированы для решения трехмерных задач.
В 1951 году за создание семейства гидроинтеграторов В. С. Лукьянову присуждена Государственная премия.
После организации серийного производства интеграторы стали экспортироваться за границу: в Чехословакию, Польшу, Болгарию и Китай. Но самое большое распространение они получили в нашей стране. С их помощью провели научные исследования в поселке «Мирный», расчеты проекта Каракумского канала и Байкало-Амурской магистрали. Гидроинтеграторы успешно использовались в шахтостроении, геологии, строительной теплофизике, металлургии, ракетостроении и во многих других областях.
Два гидроинтегратора Лукьянова представлены в коллекции аналоговых машин Политехнического музея в Москве. Это редкие экспонаты, имеющие большую историческую ценность, памятники науки и техники. Оригинальные вычислительные устройства вызывают неизменный интерес посетителей и входят в число самых ценных экспонатов отдела вычислительной техники. источник