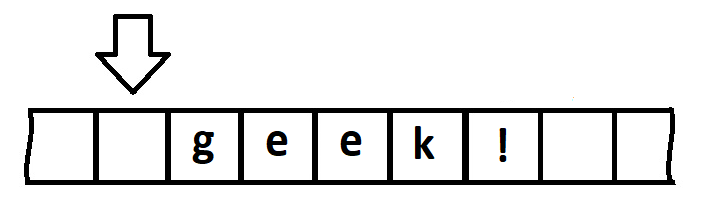Машина тьюринга простым языком
Основы теории вычислительных систем: машина с конечным числом состояний
Теория вычислительных систем — это то, что позволяет нам программировать. Однако, можно писать программы и без представления о концепциях, скрывающихся за вычислительными процессами. Не то, чтобы это было плохо — когда мы программируем, то работаем на намного более высоком уровне абстракции. В конце концов, когда мы ведём машину, то концентрируемся только на двух или трёх педалях, переключателе передач и руле. Для повседневной неспешной езды этого более чем достаточно. Однако, если мы хотим управлять автомобилем на пределе его возможностей, то тут нужно знать гораздо больше, чем просто три педали, КПП и руль.
Такой подход справедлив и в программировании. Большая часть повседневной мирской работы может быть выполнена при минимальном знании теории вычислительных систем или даже вообще без него. Не нужно понимать теорию категорий, чтобы накидать форму «Контакты» в PHP. Тем не менее, если вы планируете писать код, требующий серьёзных вычислений, то тут уж придётся разобраться с тем, что у этих самых вычислений под капотом.
Цель этой статьи — представить некоторые фундаментальные основы вычислений. Если это окажется интересным, то в дальнейшем я могу написать более продвинутый топик на эту тему, но прямо сейчас я хочу просто рассмотреть логику простейшего абстрактного вычислительного устройства — машины с конечным числом состояний (finite state machine).
Машина с конечным числом состояний
Машина с конечным числом состояний (finite state machine, FSM), или конечный автомат (finite automaton) — это математическая абстракция, используемая при проектировании алгоритмов. Говоря простым языком, машина с конечным числом состояний умеет считывать последовательности входных данных. Когда она считывает входной сигнал, то переключается в новое состояние. Куда именно переключится, получив данный сигнал, — заложено в её текущем состоянии. Звучит запутанно, но на самом деле всё очень просто.
Представим устройство, которое читает длинную бумажную ленту. На каждом дюйме этой ленты напечатана буква — a или b.
Как только устройство считывает букву, оно меняет своё состояние. Вот очень простой граф переходов для такой машины:
Кружки — это состояния, в которых машина может быть. Стрелочки — переходы между ними. Так что, если вы находитесь в состоянии s и считываете a, то вам необходимо перейти в состояние q. А если b, то просто остаётесь на месте.
Итак, если изначально мы находимся в состоянии s и начинаем читать ленту из первого рисунка слева направо, то сначала будет прочитана a, и мы переместимся в состояние q, затем b — вернёмся обратно в s. Следующая b оставит нас на месте, а a вновь переместит в q. Элементарно, но какой в этом смысл?
Оказывается, если пропустить ленту с буквами через FSM, то по её итоговому состоянию можно сделать некоторые выводы о последовательности букв. Для приведённго выше простого конечного автомата финальное состояние s означает, что лента закончилась буквой b. Если же мы закончили в состоянии q, то последней на ленте была буква a.
Это может показаться бессмысленным, но существует масса задач, которые можно решить с помощью такого подхода. Простейший пример: определить, содержит ли HTML-страница следующие теги в заданном порядке:
Также конечный автомат может использоваться для представления механизмов парковочного счётчика, автомата с газировкой, автоматизированного газового насоса и тому подобных штук.
Детерминированная машина с конечным числом состояний (Deterministic Finite State Machine)
Машины с конечным числом состояний, которые мы рассматривали выше, являются детерминированными. У них из любого состояния существует только один переход для любого разрешённого входного сигнала. Другими словами, не существует двух различных путей из данного состояния, когда вы считываете, допустим, букву a. На первый взгляд такое ограничение кажется глупым.
Недетерминированная машина с конечным числом состояний (Nondeterministic Finite State Machine)
Итак, надо распознать букву a с последующим нулём или более одинаковых букв b или c и с замыкающей следующей буквой алфавита. Самый простой способ отобразить этот алгоритм с помощью машины с конечным числом состояний представлен ниже. Финальное состояние t означает, что строка была принята целиком и соответствует шаблону.
На этом принципе основан алгоритм большинства шахматных программ. Они просматривают все возможности всех возможных ходов на данном этапе и выбирают ту стратегию, которая в данный момент даёт максимальное преимущество над противником.
Регулярные выражения
Если вы когда-нибудь занимались любым видом программирования, то вы почти наверняка сталкивались с регулярными выражениями (regular expressions). Регулярные выражения и машины с конечным числом состояний функционально эквивалентны. Всё, что можно допустить для (или связать с) регулярным выражением, можно допустить для (или связать с) конечным автоматом. Например, шаблон, который мы разбирали выше, можно связать с
Это положение известно как лемма о накачке для регулярных языков. Её основная мысль: если ваш шаблон имеет блок, который может быть повторён более, чем один раз, то этот шаблон не является регулярным. Другими словами, ни регулярные выражения, ни машины с конечным числом состояний не могут быть сконструированы так, чтобы распознавать все строки, которые можно связать с шаблоном.
Машина Тьюринга
Так как же нам распознавать нерегулярные шаблоны? Существует теоретическое устройство, подобное конечному автомату и называемое машиной Тьюринга (Turing Machine). Как и у машины с конечным числом состояний, у него имеется бумажная лента, с которой оно считывает информацию. Однако, машина Тьюринга также способна записывать и стирать данные на ленте. Полное объяснение принципов этого устройства займёт больше места, чем у нас здесь имеется, поэтому я обозначу лишь несколько важных моментов, относящихся к нашей дискуссии о машинах с конечным числом состояний и регулярных выражениях.
Машина Тьюринга вычислительно полна, и всё, что в принципе может быть вычислено, может быть вычислено с помощью машины Тьюринга. А благодаря способности записывать данные на ленту с такой же лёгкостью, как и считывать их с ленты, она не ограничена конечным числом состояний. Бумажную ленту можно представить, как имеющую бесконечную длину. Очевидно, что современные компьютеры не обладают бесконечным количеством памяти, однако, они имеют её достаточно, чтобы вы не вышли за предел для тех типов задач, которые они способны обработать.
Машина Тьюринга предоставляет нам воображаемое механическое устройство, позволяющее визуализировать и понять, как работает вычислительный процесс. Это особенно полезно для понимания пределов вычислений. Если это интересно, то в будущем я могу написать отдельную статью о машине Тьюринга.
Почему это имеет значение?
Понимание, что машины с конечным числом состояний и регулярные выражения функционально эквивалентны, открывает невероятно интересные способы применения движков регэкспов. Особенно, когда дело доходит до создания бизнес-правил, которые могут быть изменены без перекомпиляции всей системы.
Знание основ теории вычислительных систем позволяет вам брать проблему X, которую вы понятия не имеете как решать, и применять к ней подход: «Я не знаю, как решить X, но я знаю, как решить Y и как привести решение для Y к решению для X. Вот почему теперь я знаю, как решить X».
Машина Тьюринга — одно из самых важных открытий XX века
Тема: Наука
В 30-е годы XX века английский математик Алан Тьюринг придумал такое странное устройство, которое теперь называют машиной Тьюринга.
Идея его была в том, чтобы придумать устройство, абстрактную машину, которая может делать все, что вообще могут делать машины. Он был не единственным в этот момент, другие люди тоже в других терминах определяли похожие вещи, но в гораздо более абстрактных терминах, по крайней мере, в их работах конкретного механизма работы машины не было.
Факт №1
Оказалось же, что это одно из самых важных открытий XX века. То, что сейчас в разных устройствах — скажем, в телевизоре и в стиральной машине, — может использоваться одна и та же микросхема процессора, — это воплощение одной из идей Тьюринга.
И то, что одна и та же программа может использоваться в самых разных компьютерах, работать с самой разной аппаратурой и выглядеть одинаково, это тоже его идея. Тогда это называлось идеей хранимой программы (программа хранится в памяти и определяет поведение машины), и ещё была идея универсальной машины, — есть машина, которая может делать все, что может делать любая другая машина.
Если бы не Тьюринг, наверно, это придумал бы кто-то другой, он не был единственным, кто над этим работал, но так или иначе такое абстрактное теоретическое устройство оказалось одним из самых важных изобретений в XX веке.
Факт №2
Интересно, что потом Тьюринг, когда настали трудные времена, не только занимался теорией, но и практически участвовал в разных важных проектах.
Он с коллегами расшифровал коды немецкой армии — это известная история. Там использовались шифровальные машины «Энигма», которые пытались расшифровать сначала польские криптографы, а потом английские — при активном участии Тьюринга, и им это удалось.
А после войны Тьюринг уже строил реальную электронную вычислительную машину. Хотя прямой связи с его теоретическими работами не было, но явно это было продолжением той же самой деятельности. Так что хорошая теория — вещь очень практичная, и не надо бояться того, что теоретические работы окажутся бесполезными.
Факт №3
Сейчас это большая наука, которая называется теория сложности вычислений, в ней много всего интересного открыли, но есть самая главная проблема, которая называется проблема перебора, и которая до сих пор не решена.
Ее можно объяснить на таком примере: выпускалась игрушка Eternity — это такая коробочка, в которую уложены плитки, раскрашенные в разные цвета, но они раскрашены так, что видно, какие плитки можно прикладывать друг к другу (там рисунок на краях). Продаются они рассыпанными, и фирма, которая их изготовила, утверждает, что все это можно собрать в одну картинку внутри этой квадратной коробки (там 256 плиток) — то есть что изначально это была одна картинка, разрезанная на плитки.
По современным представлениям, машины такие задачи за обозримое время решать не могут, никакого способа, кроме как перебирать все варианты (а их очень много) сейчас не известно. Но, с другой стороны, никто этого не может и доказать. Это и называется проблемой перебора — доказать, что такой полный перебор каких-то объектов нельзя заменить никаким более коротким вычислением.
Факт №4
В 2000-м году был публично объявлен «список проблем следующего тысячелетия», за которые Институт Клея обещает миллион долларов.
Так вот, первая проблема в этом списке — это проблема перебора, и она там заслуженно. Интересно в теории сложности вычислений то, что не только наличие какого-то алгоритма полезно практически, но, как ни странно, часто бывает полезно отсутствие алгоритма.
Например, есть такой известный вопрос о разложении чисел на множители. Если число небольшое, то легко проверить, что оно простое — можно проверить все меньшие числа, и понять, что там нет делителей. Если число большое, то так просто уже нельзя проверить — но существуют разные алгоритмы, которые позволяют это делать. (Они основаны на малой теореме Ферма и её усовершенствованиях, но это отдельная тема.)
Так или иначе, алгоритмы проверки простоты существуют. А теперь другая задача: возьмём два больших простых числа и их перемножим, сообщим, что у нас получилось, и спросим, какие это были числа. Это задача разложения на множители, и никто не знает, как это быстро сделать. И то, что этого никто не знает, очень хорошо, потому что благодаря этому существует вся вычислительная криптография, это одно из основных её предположений.
Когда кто-нибудь снимает деньги в банке, или в Интернете заходит на сайт с помощью SSL — используются системы криптографии, основанные на том, что быстро разлагать на множители числа нельзя. Если кто-нибудь в какой-то момент обнаружит, что разлагать можно, то, думаю, после этого будет экономический кризис, потому что вся банковская система рухнет, пока люди не заменят это чем-то другим (вообще без использования компьютеров или с какими-то новыми алгоритмами).
Так что отсутствие алгоритма может быть полезнее, чем его наличие. К сожалению, никто не может доказать, что алгоритма нет, хотя все подозревают, что это так — не решена ни общая проблема перебора, ни этот частный ее случай (разложение чисел на множители), особенно важный, и про него тоже все думают, но никто ничего не придумал.
Факт №5
Что такое случайность? Это дело тонкое, вообще, существует ли случайность? Когда в каком-нибудь казино играют в рулетку — может ли наука предсказать, что там выпадет, и как нужно играть, чтобы выиграть, или это в принципе невозможно?
Федор Михайлович Достоевский твердо верил, что если быть хладнокровным и не волноваться во время игры, то можно выиграть, — он говорил, что, к сожалению, ему не удаётся быть хладнокровным, и поэтому он всё время проигрывал.
С другой стороны, теория вероятностей основана на том, что такой системы не существует, что последовательность бросания монеты в какой-нибудь игре, или последовательность выпадения красного и черного в рулетке, случайны и непредсказуемы. Но возникает вопрос, что такое случайность? Как определить, что это значит? Можем ли мы отделить случайное от неслучайного?
Сейчас вы видите две последовательности:
Вам сказано, что одна из них получена бросанием монеты, а другая как-то иначе. Сможете ли вы определить, какая из них получена каким образом?
Я думаю, что сможете, и что более-менее всякий человек, который посмотрит на эту картинку, скажет, что первая последовательность получена не бросанием монеты, а просто чередованием 0 и 1, а вторая вполне может быть получена бросанием монеты.
Но спрашивается, в чём разница? Почему вы смотрите на эту картинку и уверены, что первая последовательность не может быть получена бросанием монеты? Почему монета не может выпасть сначала орлом, потом решкой, потом снова орлом… как это объяснить? Можно сказать так: вероятность того, что это случайно произойдет, очень мала, потому что такая последовательность всего одна, а всего последовательностей очень много. Но ведь то же самое можно сказать и про вторую последовательность, появление конкретно этой последовательности имеет ту же самую малую вероятность, что и для первой. Поэтому вопрос — в чём тут разница, чем первая последовательность «лучше» второй (менее случайна, чем вторая)?
Факт №6
Или другой парадоксальный пример. Представьте себе, как в XIX веке (это написано у Лотмана в его «Беседах о русской культуре») играли в карты. В отличие от нынешней ситуации, когда карты тасуют, тогда карты продавались уже перетасованными заранее.
Поэтому дворяне, которые играли в серьезные игры, каждый раз брали новую колоду и играли с ней. После этого она выбрасывалась и поступала, как пишет Лотман, в распоряжение слуг, которые играли в своего «подкидного дурака».
Так вот, представим себе, что есть фабрика, которая выпускает такие перетасованные колоды и есть машина, которая печатает карты, а есть, которая их тасует — эта машина их как-то внутри себя тасует, потом выкладывает, запаковывает, и они поступают в продажу. Теперь представим себе, что на этой фабрике есть, как говорили в советское время, «отдел технического контроля», который должен проверять, хорошо ли они перетасованы.
Время от времени он из пачки сделанных колод достаёт одну колоду, распаковывает и смотрит, хорошо ли она перетасована. С одной стороны, он должен что-то контролировать, то есть если он никогда никакие колоды не будет браковать как негодные, то зачем он вообще нужен? А с другой стороны, непонятно, что он может контролировать, потому что вся идея того, что карты хорошо перетасованы, состоит в том, что все варианты, все возможные последовательности карт в колоде, имеют совершенно одинаковую вероятность.
Соответственно, ни одна из них, с точки зрения тасовальной машины, не лучше другой. Почему же мы некоторые колоды (некоторые последовательности карт) бракуем, а некоторые оставляем? Это как-то загадочно.
Если, скажем, все карты идут в порядке возрастания их значения, или сначала идут все красные карты, а потом черные — такие комбинации, вроде бы, надо браковать. Но, с другой стороны, непонятно, чем они хуже других. Одной из попыток ответить на этот вопрос (60-е годы XX века) было понятие сложности, то, что сейчас называется колмогоровская сложность или алгоритмическая сложность.
Факт №7
Идея эта совсем простая — что первая из последовательностей
потому выглядит неслучайной, что она проста. «Проста» значит, что существует очень короткий способ объяснить, как она устроена — сказать, что там нули и единицы чередуются. В нашем примере такая разница, может, не сильно заметна — но если там будет тысяча чередующихся нулей и единиц, то ясно, что короче это объяснить словами, чем выписывать всю последовательность.
А для настоящей случайной монеты (как считается в рамках этого объяснения случайности) — никакого способа описать последовательность более коротким способом, чем показав просто все нули и единицы, как они есть, не существует.
Можно сказать, что, если мы начнем «сжимать» последовательности каким-то архиватором, то вторая последовательность не сожмётся, а первая сожмется.
В этом и состоит основная идея Колмогорова и его коллег, которые придумали, что сложность последовательности — это длина кратчайшей программы, которая такую последовательность может напечатать, а случайные последовательности отличаются от неслучайных тем, что нельзя их напечатать никакой программой, которая короче, чем сама последовательность.
Теперь целая наука на эту тему возникла, она называется алгоритмическая теория информации, алгоритмическая случайность, но, конечно, многие вопросы там еще не ясны. Не ясен вопрос о том, что можно сделать с ограничением на сложность вычислений.
Возможно, что последовательность на самом деле неслучайна и имеет какое-то короткое описание, но мы его просто не знаем и не можем найти — или проблема может быть не в том, что мы его не можем найти, а в том, что для того, чтобы восстановить последовательность по этому описанию, нужно очень много времени.
Вот это такая активно развивающаяся и, к сожалению, ещё не очень развитая область, и там, может быть, что-нибудь интересное в ближайшее время (или не в ближайшее время) откроют.
Если вы хотите получать больше статей, подобно этой, то кликните Recommend ниже.
Наследие Тьюринга: машина, тест и полнота
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
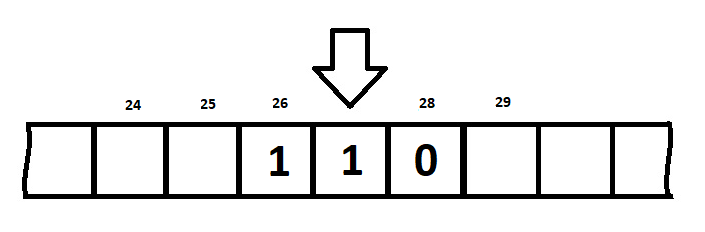
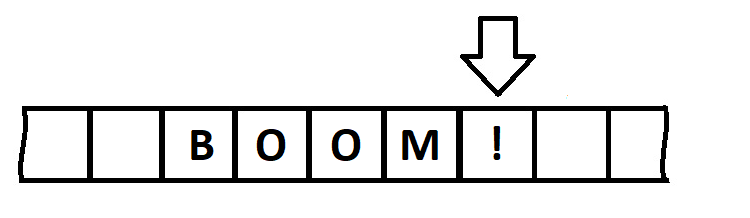
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Если вы не учились профессии программиста в вузе или не ходили в специальную школу, то, возможно «Машина Тьюринга» для вас просто дешифратор из курса истории или фильма «Игра в имитацию». В действительности всё немного сложнее, любому уважающему себя программисту необходимо знать и понимать, что это такое.
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.