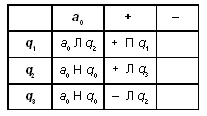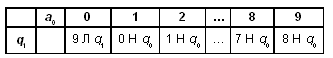Машина тьюринга стирает слово
Машина тьюринга стирает слово
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
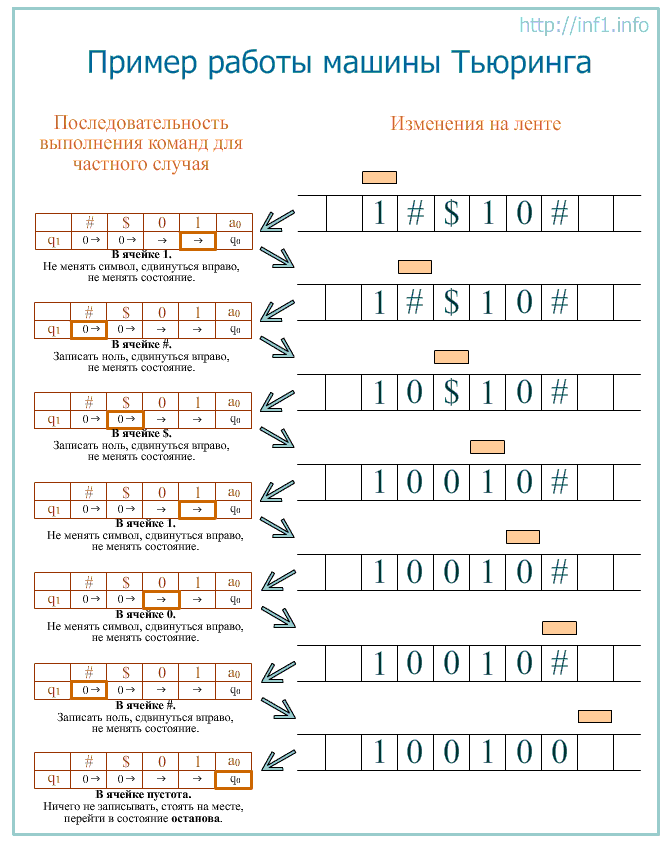
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A=
Q=
Каждая ячейка ленты может содержать символ из внешнего алфавита A =
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q =
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «
Машина Тьюринга. Удаление подслова.Как его правильно провести?
По заданию необходимо удалить из текста подслова вида ‘abc’.
Понимаю, что сначала нужно прочитать текст, чтоб найти данные подслова. Затем, обнаружив их пометить-обозначить, например как 123, и только после этого удалять.
Машина Тьюринга. Нужно правильно вычислить функцию f(x;y)=x+2y
В машине тьюринга вычислить функцию. Алгоритм выполнения есть, необходимо скинуть файл с ее.
Машина Тьюринга. Нужно правильно вычислить функцию f(x;y)=2x+y
Нужно правильно вычислить функцию f(x;y)=2x+y. Благодарю заранее)
Какую функцию f (x,y) правильно вычисляет машина Тьюринга с программой
ТЕСТ:(можно с решением) Какую функцию f (x,y) правильно вычисляет машина Тьюринга с программой
Машина Тьюринга. Приписать слева к непустому слову P его первый символ
Помочь найти в интернете решение задачи. А=
Даже помечать цифрами ничего не надо. После того, как нашли подстроку abc, поставить в текущую позицию пробел (то есть стереть «c»), а потом сделать два шага назад, на каждом шагу заменяя букву на пробел. Потом вернуться назад к первой букве после стёртого «abc» и продолжить поиск.
Машина Тьюринга: Удалить из слова Р его второй символ, если такой есть
Машина Тьюринга 1. А=
Решение задач. Машина Тьюринга
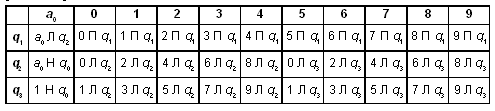
Написать программу на машине Тьюринга, прибавляющую число 2 к введенному числу.
Написать на машине Тьюринга программу, прибавляющую 3 к введенному числу.
Перенести первый символ непустого слова P в его конец. Алфавит : A=
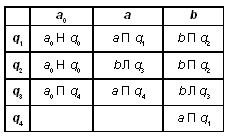
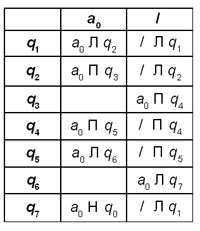
Если первый символ – это a, то надо перейти в состояние q2, в котором автомат бежит вправо и записывает в конце a. Если же первым был символ b, тогда надо перейти в состояние q3, где делается всё то же самое, только в конце записывается символ b. Если же первым был символ c, тогда переходим в состояние q4, в котором автомат дописывает за входным словом символ c.
Для решения этой задачи предлагается выполнить следующие действия:
В противном случае уничтожить всё входное слово ( q 7 ).
Запомнить первый символ, стереть второй символ и установить на его месте первый.
Сдвиг символов осуществляется так: в очередной клетке записываем b (если в q 1 ) или c (если в q 2 ), переходим вправо и меняем состояние на q 1 (если в текущей клетке было записано b ) или на q 2 (если было записано c ), где осуществляется дальнейшая запись. Если в очередной клетке записано a или пробел, то записываем в нее запомненный символ и останавливаем программу.
После этого возвращаемся к началу входного слова.
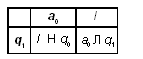
Вначале записываем знак = за входным словом. Затем возвращаемся под первый символ входного слова.
Машина тьюринга стирает слово
Абстрактные вычислительные машины
Материал взят с ресурса Планета информатики
То есть, всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:
Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).
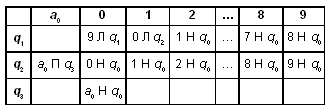
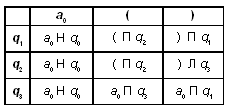
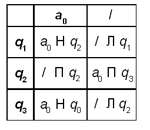
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):
Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние Q2 (команды которого совпадают с командами Q1 предыдущей программы).
Материал взят с ресурса Планета информатики
Решение этой задачи аналогично рассмотренному выше примеру.
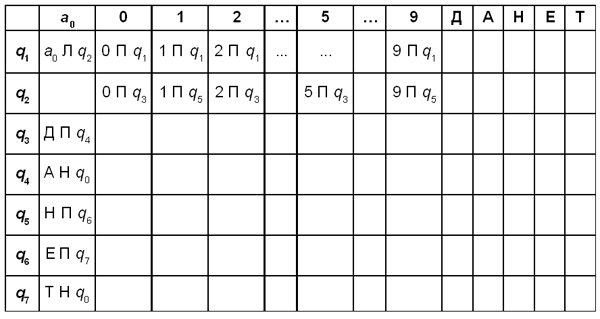
Задача 4 (усложнение задачи 3)
Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.
Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:
Рассмотрим следующие варианты входных слов:
Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.
В этом случае их программа выглядит следующим образом:
На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!
Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.
Идея решения (условие останова). На ленте есть два исходных массива штрихов.
Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.
При решении этой задачи следует обратить внимание на правильное выписывание алфавита:
Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и её начальное состояние (то есть состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из пронумерованных не обязательно упорядоченных строк команд, если в каждой команде указана строка, на которую нужно перейти. Обычно принимается, что если в команде переход не указан, то переход происходит на следующую строку. Каждая команда имеет следующий синтаксис:
После программы запуска возможны варианты:
Навигация
Календарь
Машина Тьюринга. Задачи и решения
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A=
Q=
Каждая ячейка ленты может содержать символ из внешнего алфавита A =
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q =
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «