Механическая вычислительная машина арифмометр
Знакомьтесь: арифмометр «Феликс»
Привет! На связи Музей Яндекса.
Во время режима социальной изоляции мы, как и многие коллеги по музейному делу, скучаем по посетителям:
Знакомьтесь, «Феликс» — арифмометр, один из самых популярных экспонатов нашего музея. Мало кому удаётся пройти мимо и не попытаться разобраться, как он работает. А я — Александр Шмелёв, сотрудник Музея. Под катом покажу как устроен наш «Феликс», немного первых арифмометров и много видео!
Немного истории
Арифмометр — настольная (или портативная) механическая вычислительная машина, предназначенная для выполнения точных умножения и деления, а также сложения и вычитания. Первые механические счётные машины появились ещё в XVII веке:
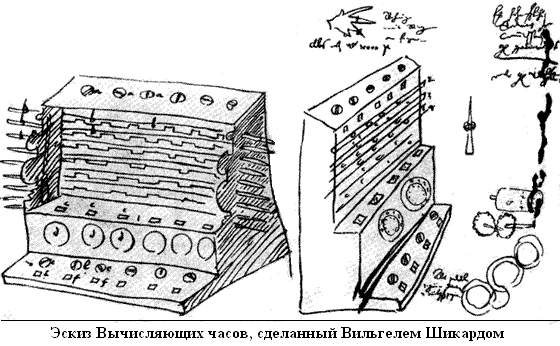
— «считающие часы» Вильгельма Шиккарда, 1623 год
Механизм состоял из звёздочек и шестерёнок, напоминающих часы, отсюда и название. Работали с шестиразрядными числами и могли выполнять все 4 операции. Со звуковым оповещением: о выходе результата вычислений за пределы технических возможностей аппарата предупреждал звонок. Два изготовленных экземпляра сгорели, а чертежи были утеряны и найдены только в 1935 году.

Реплика арифмометра Шиккарда
— суммирующая машина Блеза Паскаля («Паскалина»), 1642 год
Внешне — ящик с большим количеством шестерёнок. Хотя конструкция позволяла производить все 4 операции, удобно работать было только со сложением. Широкого распространения она не получила, но принцип работы (связанные шестерёнки) стал самым популярным для счётных машин ближайших трёх столетий.

«Паскалина» в Музее искусств и ремёсел в Париже
— арифмометр Готфрида Вильгельма Лейбница, 1673 год
Лейбниц придумал использовать шаговый барабан — колесо Лейбница. Позднее оно вошло в конструкцию популярного карманного арифмометра Curta («математическая граната»), выпускавшегося с 1948 по 1970 год. Как это выглядело:

Реплика арифмометра Лейбница
Модель колеса Лейбница
Прямым предком «Феликса» можно считать арифмометр, придуманный Вильгодтом Теофилом Однером, шведско-русским механиком и изобретателем. Он выпускался промышленно в Санкт-Петербурге с 1890 по 1918 год и известен под фамилией автора.

Арифмометр Однера
Самым важным новшеством в конструкции стало колесо Однера — подвижный диск с рычажками и штырьками. При перемещении рычажков штырьки выходят из своих гнезд, причём количество выдвинутых штырьков определяется положением рычажка. Арифмометр позволял выполнять 4 операции: сложение, вычитание, умножение и деление.

Колесо Однера
После Октябрьской революции 1917 года, наследники Однера вернулись в Швецию и стали производить вычислитель под маркой «Original-Odhner». В 1924 году петербургский завод был перевезён в Москву, и арифмометр стал «Феликсом».
Принцип работы на видео (осторожно, английский!):
«Феликс» — в честь Феликса Дзержинского
Под этим именем с 1929 по 1978 год было выпущено несколько миллионов экземпляров. Производством «Феликсов» занимались заводы счётных машин в Курске («Счётмаш»), Пензе (Пензенский завод вычислительной техники) и Москве (Завод счётно-аналитических машин имени В. Д. Калмыкова (САМ)). Кстати, «САМ» также занимался производством электронных вычислительных машин, таких как Урал-1, Стрела и БЭСМ-6.
В 70-ые годы «Феликс» стоил примерно 10–15 рублей, и за счёт достаточно низкой цены пользовался определённой популярностью: электрические калькуляторы в это же время стоили в несколько раз дороже. Арифмометрами учили пользоваться даже в школах. Почувствовать себя в роли оператора арифмометра можно тут: ссылка ведёт на инструкцию по эксплуатации.

«Феликс» на YaTalks 2019
На фото — экземпляр из коллекции Виктора Боева на YaTalks 2019. Если вы были в нашем музее до февраля текущего года, то видели именно этот арифмометр. Всем хотелось его потрогать (думаем, всё дело в его нечеловеческом обаянии), и мы решили обзавестись своим:
Органы управления арифмометром:
1 — барашек сброса счётчика оборотов ручки;
2 — счетчик оборотов основной рукоятки 10;
3 — рукоятка сдвига каретки;
4 и 7 — стрелки-запятые, не связаны с механизмом арифмометра;
5 — задвижка для сброса в 0 положений рычажков 8;
6 — счетчик результата;
8 — рычажки барабана, с помощью которых выставляется значение операнда;
9 — барашек сброса счётчика результата;
10 — основная рукоятка. На корпусе справа от рычажков 8 есть подсказка по нужному направлению вращения основной рукоятки 10 при разных арифметических операциях.
Что внутри?
Наш «Феликс» серого цвета выпущен заводом Счётмаш в городе Курск — на корпусе выбит соответствующий логотип — заглавная «С» в рамке. Сделан в 70-ые, последние годы выпуска — указан ГОСТ 16346-70. Габариты: 320х155х135 мм. Масса: 3,5 кг.
Мне удалось приобрести его в хорошем состоянии: рукоятки вращались нормально, рычажки двигались чётко, счётчики не заедали. Единственная возникшая проблема — тугая каретка. Значит, разбирать и смотреть. Поделюсь опытом: вдруг вам тоже посчастливится препарировать что-нибудь подобное.
Для обслуживания арифмометра я приготовил:
— набор шлицевых отверток;
— бумажные салфетки;
— салфетки из нетканого материала;
— машинное масло;
— ватные палочки;
— баллон со сжатым воздухом;
— бензин «Калоша».
Чтобы снять заднюю крышку, откручиваем 4 винта:
Снимаем крышки каретки:
Переворачиваем арифмометр и откручиваем ещё 6 винтов:
Отсоединяем часть с колесами Однера и основной рукояткой:
1 — система зубчатых колес Однера; 2 — счётчик результата; 3 — счётчик оборотов основной рукоятки; 4 — звонок переполнения или отрицательного числа в счётчике результата.
Откручиваем фиксаторы каретки и отсоединяем её:
На этом этапе будет много пыли и других возможностей запачкаться — не забудьте подготовиться! Продуваем и протираем внутренности. Смазываем машинным маслом трущиеся поверхности каретки и можно собирать всё в обратной последовательности.
«Феликс» позволяет работать с числами до 9 знаков. Есть и другие технические ограничения: результаты сложения, вычитания и умножения не должны превышать 13 знаков, деления — 8. При переполнении счётчика результата или получении отрицательного числа звучит звонок: требуется отменить предыдущую операцию.
Для подготовки к работе:
Так работает колесо Однера нашего «Феликса»:
ЭВМ: ЧТО? ГДЕ? КОГДА? | Арифмометр
Настольная или портативная : Чаще всего арифмометры были настольные или «наколенные» (как современные ноутбуки), изредка встречались карманные модели (Curta). Этим они отличались от больших напольных вычислительных машин, таких как табуляторы (Т-5М) или механические компьютеры (Z-1, Разностная машина Чарльза Бэббиджа).
Механическая: Числа вводятся в арифмометр, преобразуются и передаются пользователю (выводятся в окнах счётчиков или печатаются на ленте) с использованием только механических устройств. При этом арифмометр может использовать исключительно механический привод (то есть для работы на них надо постоянно крутить ручку. Этот примитивный вариант используется, например, в «Феликсе») или производить часть операций с использованием электромотора (Наиболее совершенные арифмометры — вычислительные автоматы, например «Facit CA1-13», почти при любой операции используют электромотор).
Точное вычисление: Арифмометры являются цифровыми (а не аналоговыми, как например логарифмическая линейка) устройствами. Поэтому результат вычисления не зависит от погрешности считывания и является абсолютно точным.
Умножение и деление: Арифмометры предназначались в первую очередь для умножения и деления. Поэтому почти у всех арифмометров есть устройство, отображающее количество сложений и вычитаний — счётчик оборотов (так как умножение и деление чаще всего реализовано как последовательное сложение и вычитание; подробнее — см. ниже).
Сложение и вычитание: Арифмометры могут выполнять сложение и вычитание. Но на примитивных рычажных моделях (например, на арифмометре «Феликс») эти операции выполнялись очень медленно — быстрее, чем умножение и деление, но заметно медленнее, чем на простейших суммирующих машинах или даже вручную.
Непрограммируемый: При работе на арифмометре порядок действий всегда задаётся вручную — непосредственно перед каждой операцией следует нажать соответствующую клавишу или повернуть соответствующий рычаг. Это особенность арифмометра не включается в определение, так как программируемых аналогов арифмометров практически не существовало.
Важнейшие события истории развития
Примерно VI век н.э.
Появляются китайские счёты.
Первая счётная машина (Германия, Вильгельм Шиккард). Состоит из отдельных устройств — суммирующего, множительного и записывающего. Об этом устройстве почти ничего не было известно до 1957 года, поэтому существенного влияния на развитие счётного машиностроения оно не оказало. 1642 г.
1846 г.
Счислитель Куммера (Российская империя, Польша). Он сходен с машиной Слонимского (1842, Российская Империя), но компактнее. Был широко распространён во всём мире вплоть до 1970-х годов в качестве дешёвого карманного аналога счёт.
1885 г.
Burroughs (США, У. Бэрроуз) Первая двухпериодная суммирующая машина с полноклавишным вводом и печатающим устройством.
Одновременно Mercedes-Euklid (Мерседес-Евклид), модель I» является первым (или, по крайней мере, одним из первых) арифмометров с полуавтоматическим делением (машина способна автоматически вычислять текущую цифру частного).
1950-е гг.
Расцвет вычислительных автоматов и полуавтоматических арифмометров. Именно в это время выпущена большая часть моделей электрических вычислительных машин.
1969 г.
Пик производства арифмометров в СССР. Выпущено около 300 тысяч «Феликсов» и ВК-1.
1978 г.
Примерно в это время прекращён выпуск арифмометров «Феликс-М». Возможно, это был последний в мире выпускавшийся тип арифмометров.
1995-2002 гг.
Механические кассовые аппараты (ККМ) «Ока» (модели 4400, 4401, 4600) исключены из государственного реестра РФ. Видимо, исчезла последняя область применения сложных механических вычислительных машин на территории России.
2008 г.
В некоторых магазинах Москвы ещё встречались счёты.
Справочник автора/Арифмометры
Арифмометр (в переводе с греческого — «числомер», «измеритель чисел») — механическая вычислительная машина, предназначенная для точного умножения и деления, а также для сложения и вычитания. Механическая вычислительная машина, ведущая автоматическую запись обрабатываемых чисел и результатов на особой ленте, называется арифмографом. Как правило, арифмометры были настольными, хотя встречались и портативные модели (такие как Curta)
Содержание
История [ править ]
Иногда говорят, что предтечей арифмометров был Антикитерский механизм — древнегреческий прибор для определения положения светил. Не совсем так: Антикитерский механизм — аналоговая механическая вычислительная машина (и скорее предок ПУАЗО — приборов управления артиллерийским зенитным огнём). Арифмометр — машина цифровая.
Важное отступление. В аналоговых машинах величины выставляются в непрерывном виде — как углы поворота чего-то, количество жидкости в чём-то, напряжение на чём-то и так далее. Наиболее известный аналоговый вычислитель — логарифмическая линейка: числа — длины отрезков на линейке. Аналоговые машины точны настолько, насколько точно они сделаны. Цифровые машины работают дискретными положениями каких-то элементов (цифрами), расчёты на них абсолютно повторяемы (на этом основаны запись демо-роликов и мультиплеер в Doom), а точность настолько велика, сколько цифр мы храним. Из-за точности, повторяемости и простоты программирования ход был дан именно цифровым машинам. После войны «оцифровались» и артиллерийские вычислители.
Схему первой цифровой суммирующей машины предложил Леонардо да Винчи около 1500 г. Но в то время разработка не получила распространения.
В XVII веке были сконструированы арифмометры Шиккарда, Паскаля, Лейбница и Морленда. В 1709 году появился арифмометр Полени. Серийный выпуск арифмометров начался в 1820 г. В СССР самым популярным арифмометром был «Феликс» (годы выпуска — 1929—78). Таких арифмометров было выпущено несколько миллионов.
Устройство и принцип действия [ править ]
Суммирующая машина [ править ]
Начнём с самого простого: как работает суммирующая машина. А работает она, как счётчик электричества в квартире или пробега в машине: несколько десятичных колёс, связанных механизмом переноса. Каждый раз, когда колесо прокручивается 9→0, оно зацепляет механизм переноса и сдвигает старший разряд. Чтобы не было ошибок в расчётах, колёса останавливаются не трением, а подпружиненной собачкой.
Если каким-то механизмом прощёлкивать младший разряд, получается устройство, известное под жаргонным названием кликер: с его помощью стюардессы считают пассажиров, транспортники — поток через дорогу. Но как к 123 прибавить 456? Не щёлкать же кликером 456 раз?
Первое усовершенствование — сделать по кнопочке на каждый разряд (запомним эту конструкцию под названием мультикликер). Но всё равно, чтобы набрать 456, потребуются 4+5+6=15 нажатий. Так что поступают не так: на каждый разряд делают по колесу с торчащими зубцами. Чтобы прибавить 400, надо ухватиться (пальцем или заострённым штырём) за 4-й зубец в разряде сотен и вытянуть его до самого низа. Чтобы вычесть 400 — наоборот, ухватиться за 4-й зубец сверху и толкнуть до верха.
Этот наш счётчик будем называть сумматором.
Суммирующая машина проста и дешева, некоторые варианты с полуавтоматическим переносом имели смехотворно простое устройство и умещались в кармане (счислитель Куммера).
Арифмометр «Феликс» [ править ]
Наиболее прогрессивные арифмометры (и «железный Феликс» тоже) работают на колесе Однера: на колесе вырастает от нуля до девяти зубцов в зависимости от выставленной на цифронаборнике цифры. Крутим ручку — и за один оборот арифмометр делает в точности то, что мы делали с суммирующей машиной руками. Если крутим её на оборот вперёд, прибавляется 456, если назад — вычитается. Но крутить надо точно на один оборот: если оставить в неисходном положении и начать работать с кареткой (см. ниже) или цифронаборником, можно сломать механизм (конкретно на Однере ещё и цифронаборник окажется смещённым). Потому ручка удерживается в исходном положении стопором, который надо ещё освободить (например, оттянув ручку). И крутить надо от щелчка до щелчка. Этот стопор может быть связан с блокиратором, не дающим работать с кареткой, цифронаборником и барашками сброса, если ручка не в исходном положении.
Такой способ — набрать 456 на цифронаборнике, а затем крутануть ручку — снижает вероятность ошибки (что для виртуоза суммирующей машины неважно), но несколько медленнее (что для виртуоза существенно). Потому в банках и бухгалтериях предпочитали суммирующие машины, а в конструкторских бюро — арифмометры. Но что нам этот цифронаборник даёт?
Давайте сбросим сумматор, наберём на цифронаборнике 123 и прокрутим ручку 4 раза. Что получается? 123·4=492. Уже неплохо, но как множить многозначные числа?
А для этого сумматор ставят на каретке. Она обеспечивает сдвиг результата на 1, 2, 3 и более разрядов.
Таким образом, чтобы умножить 123·456, надо действовать по принципу мультикликера: набрать на цифронаборнике 456 (так меньше работы), каретку в сотни, 1 оборот ручки, каретку в десятки, 2 оборота ручки, каретку в единицы, 3 оборота ручки.
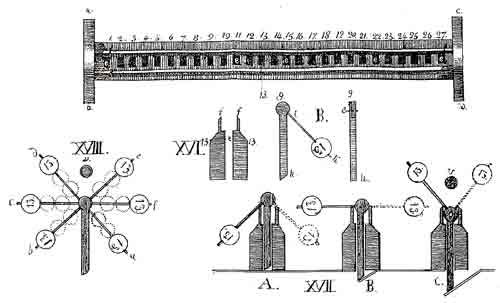
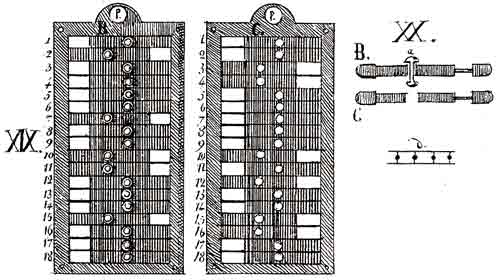
Устройство арифмометра Однера
Опытный механик поинтересуется, как устроен механизм переноса: все колёса сумматора вращаются одновременно, и традиционный шестерёнчатый перенос может просто заклинить. У Однера перенос рычажный: переход колеса через 0 взводит рычаг. Взведённый рычаг отодвигает в сторону специальный подвижный зуб на колёсах Однера, и этот зуб прибавляет единицу к следующему разряду, после этого рычаг падает. Переносы производятся не одновременно, а по очереди, от младших разрядов к старшим — тогда сложение 99+1 сначала взведёт перенос в десятки, а это, в свою очередь, перенесёт в сотни. Зубьев переноса на каждом колесе по два: для сложения и для вычитания. Кроме того, есть несколько упрощённых колёс без зубцов Однера, только с механизмом переноса: у «Феликса» их 13−9=4 штуки. Из-за такого механизма переноса запрещается возвращать недовёрнутую ручку, это приведёт к ошибке в расчётах. Надо довернуть её до конца, потом сделать оборот назад.
Наконец, в «Феликсе» есть три небольших плюшки: звонок, который звенит при переполнении от 0 до 999999 (и наоборот), маркеры-запятые, которые можно выставить так, как того требуют вычисления, и задвижка для быстрого обнуления цифронаборника (на иллюстрации её рычажок виден под эмблемой завода-изготовителя).
Сложение, вычитание и умножение мы описали. Чтобы разделить 456 на 123, надо…
Именно из-за деления в 18-ичных колёсах девятка красная: при умножении девятку обычно прокручивают как «−1, +10», а при делении надо честно прокрутить девять оборотов. Встречаются «феликсы» с одноцветным счётчиком.
Карманный арифмометр «Curta» [ править ]
Этот арифмометр стал легендой ещё до появления — разрабатывал его Курт Херцштарк в предвоенные годы. В Бухенвальде Курт восстановил чертежи по памяти, а когда пришли русские, он сбежал на западную сторону и нашёл инвестора в лице князя Лихтенштейна. «Курта» выпускалась около 30 лет, стала легендой за необычный вид и хорошее качество, и является желанным предметом для коллекционеров. Но давайте об устройстве.
Основные элементы арифмометра на месте. Цифронаборник — на внешней стороне цилиндра. Сумматор и счётчик оборотов — вверху, под ручкой. Их можно крутить относительно цифронаборника — вот вам и каретка. Механизм сброса — кольцо под ручкой, которое можно крутить в любую сторону, через сумматор или счётчик. Ручку можно слегка выдвинуть — включается вычитание (ручка крутится только вперёд).
В «Курте» используется другой принцип — он считается менее прогрессивным, чем колёса Однера, но удивительно красиво вписан в карманную конструкцию «Курты». Ручка соединена с валиком Лейбница, барабаном с 0…9 зубцами на каждой из дорожек. Работа с цифронаборником ставит зубчатое колесо напротив той или другой дорожки. В «Курте», впрочем, двадцать дорожек (плюс несколько вспомогательных), в зависимости от положения цифронаборника и переключателя «плюс-минус».
В режиме «плюс» «Курта» действует как любой арифмометр. В режиме «минус» — чтобы вычесть 456−123, дополняем разряды вычитаемого до девятки (9876), складываем (0456+9876=10332), отбрасываем лишний разряд, добавляем единицу и получаем нужные нам 333. Другими словами, «Курта» вычитает 3, прибавляя 6 (в последнем разряде прибавляется семёрка). Устроено это так: в нижнем разряде две наглухо соединённых шестерёнки, одна напротив тройки, другая — напротив двойки. В режиме сложения добавляется большее из двух (3), в режиме вычитания — тоже большее из двух (7). Дополнительный ряд из 10 зубцов используется для вычитания нуля.
За направление счётчика оборотов отвечает отдельный переключатель, действующий как XOR с ручкой: ручка в минус и счёт в минус — счёт идёт в плюс. С одной стороны, при умножении и делении нужно переключать и ручку, и переключатель направления. С другой — если вы ошиблись на единицу, вы вытягиваете ручку, не трогая переключателя, и исправляете ошибку.
У наиболее распространённой Curta 1 было 8 цифр на цифронаборнике, 6 цифр в счётчике оборотов (оснащён переносом) и 11 цифр в сумматоре.
Перенос, как и в Однере, рычажный.
Механизация [ править ]
А теперь как ускорить работу с арифмометром.
Первое, что приходит на ум,— крутить ручку электромотором. Получаются две кнопки, «+» и «−», одна эквивалентна ручке вперёд, другая — ручке назад. Иногда ухитрялись механизировать даже умножение и деление (то есть мотор даже сдвигает каретку).
Чаще используется в суммирующих машинах, чем в арифмометрах — по кнопке на разряд, как в кассовом аппарате. Штоки клавиш имеют разную длину, пропорционально величине цифр: нажатие — пружины взводятся, отпускание — колёса крутятся. Плюс очень сложный заводной механизм переноса с тремя (!) блокировками, позволяющий давить на клавиши даже одновременно: пружина переноса освободится и сделает дело, когда кнопка вернётся в исходное положение. Виртуоз суммирующей машины сделает работу даже быстрее, чем на электронном калькуляторе — потому такие машины применялись до 90-х, в то время как арифмометры в 80-е полностью исчезли.
Некоторые арифмометры отпечатывают результат на бумажной ленте.
При работе на арифмометре порядок действий всегда задаётся вручную — непосредственно перед каждой операцией следует нажать соответствующую клавишу или повернуть соответствующий рычаг. Программируемых аналогов арифмометров практически не существовало. Хотя проект первого компьютера от Чарльза Бэббиджа представлял собой именно программируемый на перфокартах арифмометр.
О том как устроено IT. Пост 1. Механические вычислительные устройства.
Итак, пилот нашел своего читателя поэтому продолжаем. В этом посте расскажу про различные механический вычислительные устройства.
Антикитерский механизм (Фрагмент A — спереди)
Антикитерский механизм (Фрагмент A — сзади)
Механизм содержал не менее 30 бронзовых шестерён в прямоугольном деревянном корпусе, на бронзовых передней и задней панелях которого были размещены циферблаты со стрелками. Две прямоугольные бронзовые защитные пластины прикрывали переднюю и заднюю панель. Ориентировочные размеры в сборе 31,5×17×6 см.
Механизм использовался для расчёта движения небесных тел и позволял узнать дату 42 астрономических событий; для вычисления лунных фаз использовалась дифференциальная передача, изобретение которой исследователи долгое время относили не ранее чем к XVI веку. Впрочем, с уходом античности навыки создания таких устройств были позабыты; потребовалось около полутора тысяч лет, чтобы люди вновь научились создавать похожие по сложности механизмы. С помощью специально разработанной компьютерной программы определено что устройство было сделано в полосе северной широты 33,3-37. Oстров Родос (36,4 с.ш.) и Сиракузы (37,1 с.ш.) часто предлагаются в качестве мест, где изготовлен или применялся антикитерский механизм.
Устройства, аналогичные антикитерскому механизму, упоминаются более чем в дюжине литературных произведений, которые написаны с 300 года до н. э. по 500 год н. э.
Первые исследования механизма проводились с 1902 по 1910 и с 1925 по 1930 годы. Уже в ходе первых осмотров прибора стало ясно, что астролябия, как некоторые изначально называли этот сложный прибор, была гораздо более продвинутой, чем любые известные астролябии. Редиадис, Радос и Теофанидис (все — греческие военно-морские офицеры и адмиралы) написали ряд статей на эту тему с 1903 по 1930 годы. Теофанидис сконструировал первую бронзовую модель астрономических часов, которые показывали некоторые из планет. Но более серьёзные результаты были получены с помощью рентгеновских исследований Прайсом в 1951—1978 годах.
В 1623 году Вильгельм Шиккард изобрел «Считающие часы» — первый арифмометр, умевший выполнять четыре арифметических действия. Считающими часами устройство было названо потому, что, как и в настоящих часах, работа механизма была основана на использовании звёздочек и шестерёнок. Это изобретение нашло практическое использование в руках друга Шиккарда, философа и астронома Иоганна Кеплера.
За Считающими часами последовали машины Блеза Паскаля («Паскалина», 1642 г.) и Готфрида Вильгельма Лейбница — арифмометр Лейбница.
Суммирующая машина Паскаля. Француз Блез Паскаль начал создавать суммирующую машину «Паскалину» в 1642 году в возрасте 19 лет, наблюдая за работой своего отца, который был сборщиком налогов и часто выполнял долгие и утомительные расчёты.
Машина Паскаля представляла собой механическое устройство в виде ящичка с многочисленными связанными одна с другой шестерёнками.
Складываемые числа вводились в машину при помощи соответствующего поворота наборных колёсиков. На каждое из этих колёсиков, соответствовавших одному десятичному разряду числа, были нанесены деления от 0 до 9. При вводе числа колесики прокручивались до соответствующей цифры. Совершив полный оборот, избыток над цифрой 9 колёсико переносило на соседний разряд, сдвигая соседнее колесо на 1 позицию. Ответ появлялся в верхней части металлического корпуса.
Несмотря на преимущества автоматических вычислений, использование десятичной машины для финансовых расчётов в рамках действовавшей в то время во Франции денежной системы было затруднительным. Расчёты велись в ливрах, су и денье. В ливре насчитывалось 20 су, в су — 12 денье. Использование десятичной системы в недесятичных финансовых расчётах усложняло и без того нелёгкий процесс вычислений. Тем не менее примерно за 10 лет Паскаль построил около 50 и даже сумел продать около дюжины вариантов своей машины. Несмотря на вызываемый ею всеобщий восторг, машина не принесла богатства своему создателю. Сложность и высокая стоимость машины в сочетании с небольшими вычислительными способностями служили препятствием её широкому распространению. Тем не менее, заложенный в основу «Паскалины» принцип связанных колёс почти на три столетия стал основой для большинства создаваемых вычислительных устройств.
Схему подобного арифмометру механизма нарисовал Леонардо да Винчи. Это устройство датируется 1500 годом и представляет собой 13-разрядную суммирующую машину на десятизубых колёсах. Однако в своё время идеи Леонардо никакого распространения не получили.
Арифмометр Лейбница. Идея создания машины, выполняющей вычисления, появилась у выдающегося немецкого математика и философа Готфрида Вильгельма Лейбница после его знакомства с голландским математиком и астрономом Христианом Гюйгенсом. Огромное количество вычислений, которое приходилось делать астроному, навело Лейбница на мысль о создании механического устройства, которое могло бы облегчить такие расчёты («Поскольку это недостойно таких замечательных людей, подобно рабам, терять время на вычислительную работу, которую можно было бы доверить кому угодно при использовании машины»).
Арифмометр был создан Лейбницем в 1673 году. Сложение чисел выполнялось в десятичной системе счисления при помощи связанных друг с другом колёс, так же как на вычислительной машине Блеза Паскаля. Добавленная в конструкцию движущаяся часть и специальная рукоятка, позволявшая крутить ступенчатое колесо (в последующих вариантах машины — цилиндры), позволяли ускорить повторяющиеся операции сложения, при помощи которых выполнялось деление и перемножение чисел. Необходимое число повторных сложений выполнялось автоматически.
Копия арифмометра Лейбница в Немецком музее.
Были построены два прототипа, до сегодняшнего дня только один сохранился в Национальной библиотеке Нижней Саксонии в Ганновере, Германия. Несколько поздних копий находятся в музеях Германии, например, один в Немецком музее в Мюнхене.
Несмотря на недостатки арифмометра Лейбница, он дал изобретателям арифмометров новые возможности. Привод, изобретённый Лейбницем — шагающий цилиндр или колесо Лейбница — использовался во многих вычислительных машинах на протяжении 300 лет, до 1970-х годов.
Лейбниц также описал двоичную систему счисления — один из ключевых принципов построения всех современных компьютеров. Однако, вплоть до 1940-х многие последующие разработки были основаны на более сложной в реализации десятичной системе.
В 1820 году Шарль Ксавье Тома де Кольмар создал первое серийно выпускавшееся механическое счётное устройство — арифмометр Томаса, который мог складывать, вычитать, умножать и делить. В основном, он был основан на работе Лейбница.
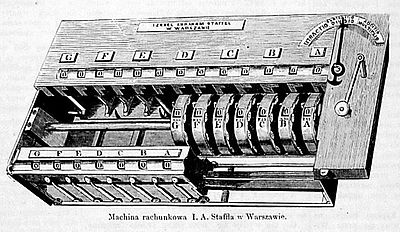
В 1845 году Израиль Штаффель представил счётную машину, которая кроме четырёх арифметических действий могла извлекать квадратные корни. Арифмометры, считающие десятичные числа, использовались до 1970-х.
Вычислительная машина Штаффеля. Ни один экземпляр машины не сохранился до XXI века. Её конструкция известна только по историческим источникам, в основном, это статьи для прессы, отчёты и решения жюри c выставок, на которых демонстрировалась машина.
Создатель машины, Израиль Авраам Штаффель, был жителем Варшавы, по профессии — часовщик. Штаффель вырос в бедной еврейской семье и не имел доступа к научным публикациям, рассказывающих о последних изобретениях Западной Европы. Выучил польский язык, что позволило ему читать научно-технические публикации по механике, издаваемые в Царстве Польском. Неизвестно, было ли ему известно о счётных машинах других варшавских изобретателей, Авраама Штерна или Хаима Слонимского, и поэтому невозможно достоверно утверждать, как те повлияли на сконструированное им устройство. Штаффель не был знаком с конструкцией арифмометра де Кольмара или других счётных машин, созданных в Западной Европе. В связи с этим следует предположить, что построенная им машина была его собственным изобретением, мало похожей на разработанные ранее вычислительные устройства. Штаффель начал строить машину в 1835 году и закончил работы через 10 лет. Впервые он продемонстрировал машину публике в 1845 году. Позже Штаффель представил ещё несколько моделей машины, содержащих различные усовершенствования. В 1845 году на промышленной выставке в Варшаве Израиль Авраам Штаффель был награждён серебряной медалью. В комитет, присуждающий медаль. В описании машины отмечалось значительное снижение времени, необходимого на выполнение вычислений по сравнению с ручными расчётами на бумаге.
В том же 1845 году Штаффель ознакомил с машиной министра народного просвещения, президента Петербургской академии наук Уварова, когда тот был в Варшаве, Уваров обещал ему содействие. После получения Штаффелем серебряной медали на выставке наместник Царства Польского Паскевич, князь Варшавский, выдал ему 150 рублей на поездку в Санкт-Петербург для представления машины в академии наук.В 1846 году Уваров поручил академии исследовать машину. По результатам исследования она получила широкое признание среди членов академии. В 1851 году машина вместе с некоторыми другими устройствами Штаффеля была представлена на Всемирной выставке в Лондоне. Машина Штаффеля получила серебряную медаль и была признана лучшей из вычислительных машин, участвовавших в выставке.
Механизм машины был основан на колесе Лейбница.
В 1804 году Жозеф Мари Жаккар разработал ткацкий станок, в котором вышиваемый узор определялся перфокартами. Серия карт могла быть заменена, и смена узора не требовала изменений в механике станка. Это было важной вехой в истории программирования.
Перфокарточная система музыкального автомата
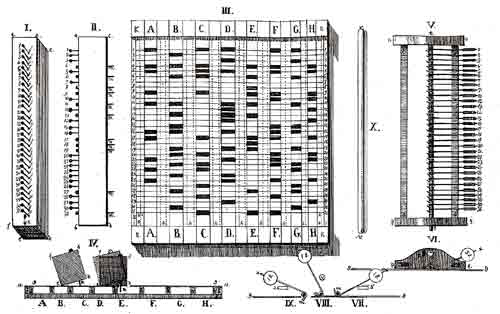
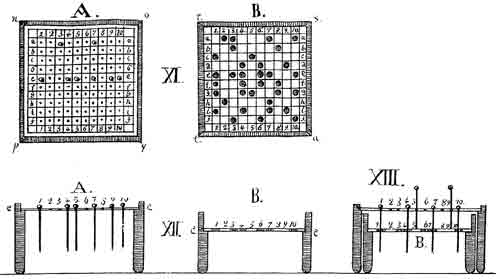
В 1832 году Семен Корсаков применил перфорированные карты в конструкции разработанных им «интеллектуальных машин», механических устройств для информационного поиска, являющихся прообразами современных баз данных и, в какой-то степени, — экспертных систем. С. Н. Корсаков является пионером русской кибернетики. Основное стремление С. Н. Корсакова — усиление возможностей разума посредством разработки научных методов и специальных устройств. В первой половине XIX века он изобрел и сконструировал ряд действующих механических устройств, функционирующих на основе перфорированных таблиц и предназначенных для задач информационного поиска и классификации.
Гомеоскоп прямолинейный с неподвижными частями. Он представляет собой наиболее простое из всех устройств Корсакова. Пользуясь им, можно найти среди большого числа записей, отображённых в гомеоскопической перфорированной таблице, ту, которая содержит все признаки другой заданной записи.
Гомеоскоп прямолинейный с подвижными частями. Он может указывать то же самое, что и гомеоскоп прямолинейный с неподвижными частями, и в дополнение к этому он находит и отделяет из заданной записи все те признаки, которые соответствуют (или не соответствуют) аналогичным признакам других записей в таблице.
Плоский гомеоскоп. Плоский гомеоскоп аналогично указывает соответствия, имеющиеся у сравниваемых между собой записей, число признаков которых может достигать многих тысяч. С. Н. Корсаков утверждает, что число признаков можно довести до одного миллиона, используя, так называемые, градуированные стержни. В целом плоский гомеоскоп позиционируется Корсаковым как устройство для обработки больших массивов данных.
Идеоскоп представляет наиболее «хитроумное» из всех пяти устройств, предложенных С. Н. Корсаковым. Идеоскоп одновременно позволяет выполнить исчисление следующих значений:
множество вообще возможных признаков, но отсутствующих в заданной и сравниваемой записях
множество признаков заданной записи, но которых нет в сравниваемой записи из идеоскопической таблицы
множество общих признаков для заданной и сравниваемой записей
множество общих наиболее важных признаков
множество наиболее важных признаков сравниваемой записи из таблицы, но которые отсутствуют в заданной записи
множество признаков сравниваемой записи из таблицы, которые отсутствуют в заданной записи.
Простой компаратор. Компаратор определяет те же операции с множествами, что и идеоскоп. Преимущество компаратора заключается в том, что признаки сравниваемых идей можно задать непосредственно (динамически) перед началом сравнения, не требуется заранее подготавливать и использовать перфорированные таблицы. Ограничение состоит в том, что за один раз возможно сравнение только двух идей.
В целом, изобретенные С. Н. Корсаковым машины позволяют быстро находить, сравнивать и классифицировать множества информационных записей (идей) по набору многочисленных признаков (деталей). C. Н. Корсаков позиционирует свои машины как усиливающие человеческий разум для одновременного охвата большого количества объектов и их сравнения по множеству признаков. Для реализации своих машин С. Н. Корсаков по существу впервые применил перфорированные карты в информатике. В работах С. Н. Корсакова содержится целый ряд новых для того времени идей, как то: многокритериальный поиск с учетом относительной степени важности различных критериев, способ обработки больших массивов данных, предтеча современных экспертных систем, и даже попытка определить понятие алгоритма.
С. Н. Корсаков предпринял два шага к продвижению своих изобретений. В 1832 г. им была издана брошюра «Начертание нового способа исследования при помощи машин, сравнивающих идеи». По традиции того времени, брошюра была написана на французском языке. В том же году С. Н. Корсаков предпринимает попытку представить свои изобретения на суд Императорской Академии наук в Санкт-Петербурге. Однако С. Н. Корсакову не повезло. Изобретения его не были в должной мере оценены современниками и не получили официальной поддержки. Заключение комиссии содержало ироническое замечание: «Г-н Корсаков потратил слишком много разума на то, чтобы научить других обходиться без разума».
В 1838 году Чарльз Бэббидж перешёл от разработки Разностной машины к проектированию более сложной аналитической машины, принципы программирования которой напрямую восходят к перфокартам Жаккара.
Разностная машина Чарльза Бэббиджа. Предназначен для автоматизации вычислений путём аппроксимации функций многочленами и вычисления конечных разностей. Возможность приближённого представления в многочленах логарифмов и тригонометрических функций позволяет рассматривать эту машину как довольно универсальный вычислительный прибор.
В 1822 году Бэббиджем была построена модель разностной машины, состоящая из валиков и шестерней, вращаемых вручную при помощи специального рычага. Заручившись поддержкой Королевского общества, посчитавшего его работу «в высшей степени достойной общественной поддержки», Бэббидж обратился к правительству Великобритании с просьбой о финансировании полномасштабной разработки. В 1823 году правительство Великобритании предоставило ему субсидию в размере 1500 фунтов стерлингов (общая сумма правительственных субсидий, полученных Бэббиджем на реализацию проекта, составила в конечном счёте 17 000 фунтов стерлингов). Разрабатывая машину, Бэббидж и не представлял всех трудностей, связанных с её реализацией, и не только не уложился в обещанные три года, но и спустя девять лет вынужден был приостановить свою работу. Однако часть машины все же начала функционировать и производила вычисления даже с большей точностью, чем ожидалось. Конструкция разностной машины основывалась на использовании десятичной системы счисления. Механизм приводился в действие специальными рукоятками. Когда финансирование создания разностной машины прекратилось, Бэббидж занялся проектированием гораздо более общей аналитической машины, но затем всё-таки вернулся к первоначальной разработке. Улучшенный проект, над которым он работал между 1847 и 1849 годами, носил название «Разностная машина № 2».
Копия разностной машины в лондонском Музее науки
Несмотря на неудачу с разностной машиной, Бэббидж в 1833 году задумался о создании программируемой вычислительной машины, которую он назвал аналитической (прообраз современного компьютера). В отличие от разностной машины, аналитическая машина позволяла решать более широкий ряд задач. Именно эта машина стала делом его жизни и принесла посмертную славу. Он предполагал, что построение новой машины потребует меньше времени и средств, чем доработка разностной машины, так как она должна была состоять из более простых механических элементов. С 1834 года Бэббидж начал проектировать аналитическую машину.
Архитектура современного компьютера во многом схожа с архитектурой аналитической машины. В аналитической машине Бэббидж предусмотрел следующие части: склад (store), фабрика или мельница (mill), управляющий элемент (control) и устройства ввода-вывода информации.Склад предназначался для хранения как значений переменных, с которыми производятся операции, так и результатов операций. В современной терминологии это называется памятью. Мельница (арифметико-логическое устройство, часть современного процессора) должна была производить операции над переменными, а также хранить в регистрах значение переменных, с которыми в данный момент осуществляет операцию. Третье устройство, которому Бэббидж не дал названия, осуществляло управление последовательностью операций, помещением переменных в склад и извлечением их из склада, а также выводом результатов. Оно считывало последовательность операций и переменные с перфокарт. Перфокарты были двух видов: операционные карты и карты переменных. Из операционных карт можно было составить библиотеку функций. Кроме того, по замыслу Бэббиджа, Аналитическая машина должна была содержать устройство печати и устройство вывода результатов на перфокарты для последующего использования.
Только после смерти Чарлза Бэббиджа его сын, Генри Бэббидж, продолжил начатое отцом дело. В 1888 году Генри сумел построить по чертежам отца центральный узел аналитической машины. А в 1906 году Генри совместно с фирмой Монро построил действующую модель аналитической машины, включающую арифметическое устройство и устройство для печатания результатов. Машина Бэббиджа оказалась работоспособной.
В 1864 году Чарлз Бэббидж написал: «Пройдёт, вероятно, полстолетия, прежде чем люди убедятся, что без тех средств, которые я оставляю после себя, нельзя будет обойтись». В своём предположении он ошибся на 30 лет. Только через 80 лет после этого высказывания была построена машина МАРК-I, которую назвали «осуществлённой мечтой Бэббиджа». Архитектура МАРК-I была очень схожа с архитектурой аналитической машины. Говард Эйкен на самом деле серьёзно изучал публикации Бэббиджа и Ады Лавлейс перед созданием своей машины, причём его машина идеологически незначительно ушла вперёд по сравнению с недостроенной аналитической машиной. Производительность МАРК-I оказалась всего в десять раз выше, чем расчётная скорость работы аналитической машины.
В 1948 году появился Curta — небольшой арифмометр, который можно было держать в одной руке. В 1950-х — 1960-х годах на западном рынке появилось несколько марок подобных устройств.