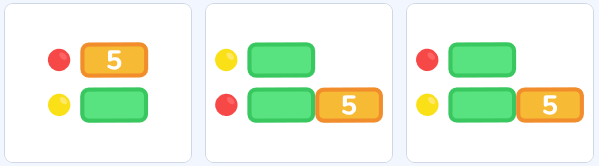
На парковке было 3 красных 4 желтых и 5 зеленых автомобиля
Головоломки для взрослых
Более 3500 логических загадок и головоломок для взрослых! Пройдите весь курс логики от ЛогикЛайк или выбирайте любимые категории головоломок.
Отгадывайте головоломки онлайн!
Решение головоломок помогает держать мозг в тонусе!
Семь головоломок для тренировки логики и мышления
Есть 5 красных шариков. Их больше, чем желтых. Выберите подходящую схему
На парковке было 3 красных, 4 желтых и 5 зеленых автомобиля.
Потом уехали восемь машин.
Какого цвета сейчас определенно меньше, чем раньше?
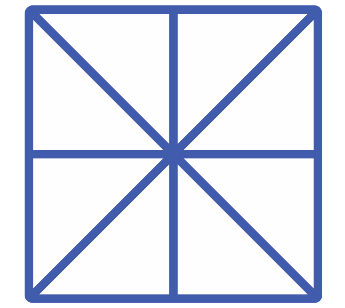
Популярная головоломка, которую дошкольники решают быстрее, чем взрослые 🙂
Сколько всего треугольников на картинке?
Арчи лгал по понедельникам, вторникам и средам и говорил правду во все остальные дни недели.
Карл лгал по четвергам, пятницам и субботам и говорил правду во все остальные дни.
Арчи: Вчера я врал.
Карл: Я тоже вчера врал.
Какой день недели был вчера?
Каждую пятницу Тим ходит в любимое кафе.
В любом месяце он посещает кафе 4 раза.
Но в некоторых месяцах пятниц больше, и Тим отдыхает чаще.
Какое наибольшее число таких месяцев может быть в году?
Более 550 000 детей и их родителей со всего мира уже развивают логику и мышление вместе с нами!
На парковке было 3 красных 4 желтых и 5 зеленых автомобиля
В фирме такси в данный момент свободно 16 машин: 4 черных, 3 синих и 9 белых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет черное такси.
вероятность того, что к заказчице приедет черное такси равна
В фирме такси в данный момент свободно 15 машин: 2 красных, 9 желтых и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
вероятность того, что к заказчице приедет желтое такси равна
Ваш ответ: 0.6. Правильный ответ: 0,6
В записи десятичной дроби используйте запятую
В фирме такси в данный момент свободно 35 машин: 11 красных, 17 фиолетовых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Вероятность того, что к заказчице приедет зеленое такси равна
В фирме такси в данный момент свободно 20 машин: 3 белых, 11 синих и 6 серых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет белое такси.
Вероятность того, что к заказчице приедет белое такси равна
Максим с папой решил покататься на колесе обозрения. Всего на колесе 30 кабинок, из них 11 – синие, 7 – зеленые, остальные – оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Максим прокатится в оранжевой кабинке.
на колесе обозрения 30–11–7=12 оранжевых кабинок. Тогда вероятность того, что Максим прокатится в оранжевой кабинке равна
Аня с папой решили покататься на колесе обозрения. Всего на колесе 22 кабинки, из них 5 — желтые, 6 — белые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Аня прокатится в красной кабинке.
На колесе обозрения 22 – 5 – 6 = 11 красных кабинок. Тогда вероятность того, что Аня прокатится в красной кабинке равна
Кирилл с папой решил покататься на колесе обозрения. Всего на колесе 30 кабинок, из них 8 – фиолетовые, 4 – зеленые, остальные – оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Кирилл прокатится в оранжевой кабинке.
На колесе обозрения оранжевых кабинок. Тогда вероятность того, что Кирилл прокатится в оранжевой кабинке равна
На парковке было 3 красных 4 желтых и 5 зеленых автомобиля
Я всегда покупаю носки десятками и одного цвета. Это практично.
Я тоже. Но вопрос в другом.
да пойду новые куплю- зачем зря заморачиваться)
Два носка. Если ты не дальтоник конечно.
3 цвета потому что.
И что? Я же слепой! Цветов не различаю!! Сами сказали!
Куча вариантов! если взять один и держать, и брать другой, то всё равно есть шанс угадать с первого раза! Или я не понял условия загадки?
Я могу взять два носка одеть не глядя
Левый и правый носок различаются?! )
А вы усложните задачку, пущай различаются. ))
А дальтоников это тоже касается?
Ja bozmy cornue hihi
На парковке было 3 красных 4 желтых и 5 зеленых автомобиля
Дайте обоснованные ответы на следующие вопросы.
а) В мешке находятся 1 желтый, 1 зеленый и 2 красных шара. Из мешка случайным образом вынимают 2 шара разного цвета и заменяют одним шаром третьего цвета. Этот процесс продолжают до тех пор, пока все оставшиеся шары в мешке не окажутся одного цвета (возможно, что при этом в мешке останется один шар) Какого цвета шары (или шар) могут остаться в мешке?
б) В мешке 3 желтых, 4 зеленых и 5 красных шаров. Какого цвета шары (или шар) могут остаться в мешке в конце после применения описанной в предыдущем пункте процедуры?
в) В мешке находятся 3 желтых, 4 зеленых и 5 красных шаров. Из мешка случайным образом вынимают 2 шара разного цвета и заменяют двумя шарами третьего цвета. Можно ли, применяя эту процедуру многократно, добиться того, чтобы в мешке оказались шары одного цвета? Если можно, то какого цвета эти шары?
а) Обозначим (Ж, З, К) упорядоченную тройку чисел, характеризующую состояние мешка на данный момент, т. е. количество жёлтых, зелёных и красных шаров в мешке. Изначально мешок находится в состоянии (1, 1, 2).
Если в первый раз из мешка вынимают жёлтый и зелёный шар и заменяют их красным шаром, то мешок переходит в состояние (0, 0, 3), когда все шары в мешке — красные. Если в первый раз из мешка вынимают зелёный и красный шар и заменяют их жёлтым шаром, то мешок переходит в состояние (2, 0, 1). Дальнейшие переходы из одного состояния в другое определяются однозначно и описываются цепочкой: (2, 0, 1)→(1, 1, 0)→(0, 0, 1) Видим, что в мешке остался красный шар. Аналогично, если в первый раз из мешка вынимают жёлтый и красный шар и заменяют их зелёным шаром, то мешок переходит в состояние (0, 2, 1). Дальнейшие переходы из одного состояния в другое определяются однозначно и описываются цепочкой: (0, 2, 1)→(1, 1, 0)→(0, 0, 1).
Видим, что в мешке снова остался красный шар. Таким образом, в любом случае оставшиеся в мешке шары (или шар) будут красными.
б) Легко видеть, что в мешке могут остаться зелёные шары: (3, 4, 5)→(4, 3, 4)→(3, 4, 3)→(2, 5, 2)→(1, 6, 1).
Докажем, что в любом случае оставшиеся в мешке шары будут зелёными. Так как каждый раз общее количество шаров в мешке уменьшается на 1, то процесс завершится не более чем за 11 шагов. В начальном состоянии количество жёлтых и красных шаров нечётно, а количество зелёных шаров — чётно. Поскольку за один ход (выемку и замену шаров) количество шаров каждого цвета изменяется на 1, количества жёлтых и красных шаров всегда будут одной чётности, а количество зелёных шаров — противоположной чётности. Поэтому, никогда нельзя получить состояние, в котором количество зелёных и количество красных шаров оба будут нулевыми, также, как никогда нельзя получить состояние, в котором количество зелёных и количество жёлтых шаров будут нулевыми. Следовательно, в любом случае в конце мы получим состояние, в котором все оставшиеся в мешке шары будут зелёными.
в) Обозначим f(С)=Ж − З, где Ж и З — количества жёлтых и зелёных шаров в данном состоянии С = (Ж, З, К). Предположим, что из состояния С за один шаг мы перешли в состояние С’ = (Ж’, З’, К’)
Докажем, что f(С) и f(С’) дают одинаковые остатки при делении на 3. Для этого покажем, что разность Δf = f(С’) ‐ f(С) делится на 3. Рассмотрим несколько случаев.
Случай 1. Ж’ = Ж −1, З’ = З − 1, К’=К + 2. Δf = f(С’) − f(С) = (Ж’ − З’) · (Ж − З) = 0.
Случай 2. Ж’ = Ж ‐ 1, З’ = З + 2, К’ = К‐1. Δf = f(С’) · f(С) = (Ж’ − З’) − (Ж − З) = −3.
Случай 3. Ж’ = Ж + 2, З’ = З − 1, К’ = К − 1. Δf = f(С’) − f(С) = (Ж’ − З’) − (Ж − З) = 3.
Видим, что f(С) и f(С’) дают одинаковые остатки при делении на 3.
Для начального состояния C0(3, 4, 5) находим: f(C0) = Ж − З = 3 − 4 = −1.
Oбщее количество шаров в мешке остаётся неизменным, поскольку каждый раз два вынутых шара заменяются двумя шарами другого цвета. Если бы в конце в мешке все шары оказались бы одного цвета, то конечным состоянием было бы одно из трёх состояний (12, 0, 0), (0, 12, 0) или (0, 0, 12).
В любом случае f(Cn) будет делиться на 3, и, значит, f(C0) и f(Cn) дают разные остатки при делении на 3. Следовательно, применяя указанную процедуру, добиться того, чтобы в мешке оказались шары одного цвета, нельзя.