На рисунке 184 изображены автомобиль и велосипедист двигающийся навстречу друг другу
Материальная точка. Система отсчета. Перемещение. Определение координаты
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
1404. Можно ли считать автомобиль материальной точкой при определении пути, который он проехал за 2 ч? за 2 с?
В первом случае можно. Во втором случае нельзя, потому что тело можно считать материальной точкой тогда, когда его размеры меньше расстояний, рассматриваемых в задаче.
1405. Можно ли рассматривать поезд длиной 200 м как материальную точку при определении времени, за которое он проехал расстояние 2 м?
Нельзя. Длина поезда больше пройденного им расстояния. Для рассмотрения поезда в качестве материальной точки расстояние, пройденное им, должно быть больше его собственной длины.
1406. Можно ли считать поезд длиной 200 м материальной точкой при определении времени, за которое он проехал мост длиной 800 м?
Можно.
1407. Муха ползет по краю блюдца из точки А в точку В (рис. 176). На рисунке покажите:
а) траекторию движения мухи;
б) перемещение мухи.
1408. При каком движении материальной точки путь, пройденный точкой, равен модулю перемещения?
При прямолинейном.
1409. Рота солдат прошла на север 4 км, затем солдаты повернули на восток и прошли еще 3 км. Найдите путь и перемещение солдат за все время движения. Нарисуйте в тетради траекторию их движения.
1410. Найдите координаты точек А, В и С в системе координат XOY (рис. 177). Определите расстояния между точками:
а) А и В, б) В и С, в) А и С.
1411. На рисунке 178 показаны перемещения трех материальных точек: s1, s2, s3. Найдите:
а) координаты начального положения каждой точки;
б) координаты конечного положения каждой точки;
в) проекции перемещения каждой точки на координатную ось OX;
г) проекции перемещения каждой точки на координатную ось OY;
д) модуль перемещения каждой точки.
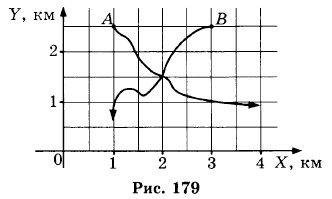
1413. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
1415. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось OX, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату x0 начального положения мяча;
б) координату xm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1416. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.
На рисунке 184 изображены автомобиль и велосипедист двигающийся навстречу друг другу
Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью
а к автобусу — со скоростью
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Не совсем понял решение. Объясните пожалуйста, как решаются подобные задачи?
Самое полезное, что можно придумать в таких задачах — нарисовать картинку, на ней обозначить вектора скоростей всех тел относительно одной системы отсчета (в данном случае, относительно Земли). А потом из рисунка уже выписывать, чему равны модули скоростей одних тел, относительно других. Например, пешеход и велосипедист двигаются навстречу, а значит, скорость их сближения — это сумма их скоростей относительно Земли: . А вот автобус нагоняет велосипедиста, поэтом его скорость относительно велосипедиста равна
. Смотрите внимательно на картинку и все поймете.
Хочу предложить другой способ решения:
1. Находим модуль скорости сближения пешехода и автобуса |v-10v|=9v.
2. Делим полученную скорость на 2, т. к. модуль скорости велосипедиста должен быть одинаков относительно пешехода и автобуса ОДНОВРЕМЕННО, т. е. 4,5v.
Судя по картинке, скорость велосипедиста относительно пешехода равна 14 км/ч, а относительно автобуса — 22 км/ч. В условии сказано, чтобы скорости велосипедиста относительно двух тел (пешехода и автобуса) должны быть равны. Так вот, они (скорости) будут равны, если скорость велосипедиста относительно поверхности будет равна 22 км/ч. Пожалуйста, не говорите, что я неправильно решил задачу))
Скорость велосипедиста относительно пешехода 18 + 4 = 22 км/ч такая же как относительно автобуса. Если тела движутся в разные стороны, то относительная скорость равна сумме скоростей, а не разности. Допустим, если два пешехода идут навстречу друг другу, то они сближаются со скоростью 4 + 4 = 8 км/ч, а не покоятся относительно друг друга (4 – 4 = 0).
На рисунке 184 изображены автомобиль и велосипедист двигающийся навстречу друг другу
Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью
а к автобусу — со скоростью
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Не совсем понял решение. Объясните пожалуйста, как решаются подобные задачи?
Самое полезное, что можно придумать в таких задачах — нарисовать картинку, на ней обозначить вектора скоростей всех тел относительно одной системы отсчета (в данном случае, относительно Земли). А потом из рисунка уже выписывать, чему равны модули скоростей одних тел, относительно других. Например, пешеход и велосипедист двигаются навстречу, а значит, скорость их сближения — это сумма их скоростей относительно Земли: . А вот автобус нагоняет велосипедиста, поэтом его скорость относительно велосипедиста равна
. Смотрите внимательно на картинку и все поймете.
Хочу предложить другой способ решения:
1. Находим модуль скорости сближения пешехода и автобуса |v-10v|=9v.
2. Делим полученную скорость на 2, т. к. модуль скорости велосипедиста должен быть одинаков относительно пешехода и автобуса ОДНОВРЕМЕННО, т. е. 4,5v.
Судя по картинке, скорость велосипедиста относительно пешехода равна 14 км/ч, а относительно автобуса — 22 км/ч. В условии сказано, чтобы скорости велосипедиста относительно двух тел (пешехода и автобуса) должны быть равны. Так вот, они (скорости) будут равны, если скорость велосипедиста относительно поверхности будет равна 22 км/ч. Пожалуйста, не говорите, что я неправильно решил задачу))
Скорость велосипедиста относительно пешехода 18 + 4 = 22 км/ч такая же как относительно автобуса. Если тела движутся в разные стороны, то относительная скорость равна сумме скоростей, а не разности. Допустим, если два пешехода идут навстречу друг другу, то они сближаются со скоростью 4 + 4 = 8 км/ч, а не покоятся относительно друг друга (4 – 4 = 0).
На рисунке 184 изображены автомобиль и велосипедист двигающийся навстречу друг другу
Решение:
Велосипедист проедет до встречи расстояние

Автомобиль проедет до встречи расстояние

Подставим выражение для х в формулу (2)
Расстояние до встречи, пройденное велосипедистом
Если скорости увеличатся в два раза, то время до встречи
Расстояние до встречи, пройденное велосипедистом
Т.е. место встречи не изменится.
Ответ: 
Материальная точка. Система отсчета. Перемещение. Определение координаты движущегося тела
1394. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
а) модуль перемещения автомобиля;
б) модуль перемещения велосипедиста;
в) проекцию перемещения каждого тела на ось ОХ;
г) путь, пройденный каждым телом;
д) расстояние между телами в начальный момент времени;
е) расстояние между телами в конечный момент времени.
1396. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось ОХ, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату х0 начального положения мяча;
б) координату хm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1397. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.