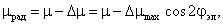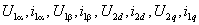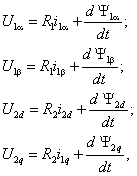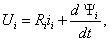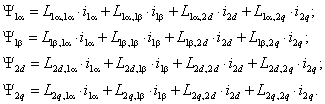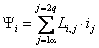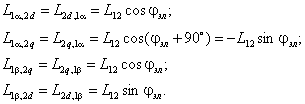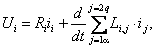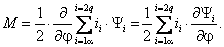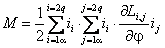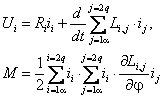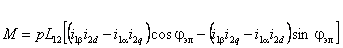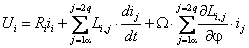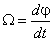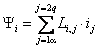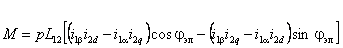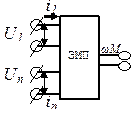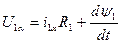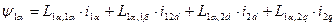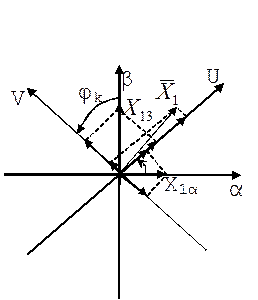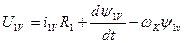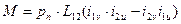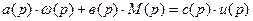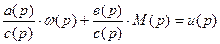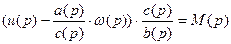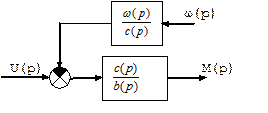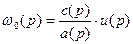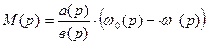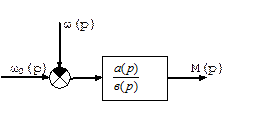Обобщенная электрическая машина как основной компонент электропривода

Обобщенная электрическая машина как основной компонент электропривода

Тема: «Краткие сведения из теории обобщенной электрической машины»

Рассматривая двигатель как элемент электромеханической системы, целесообразно механическую инерцию ротора и момент потерь на его валу отнести к механической части системы, считая механическими переменными электромагнитный момент двигателя М и скорость его ротора .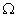

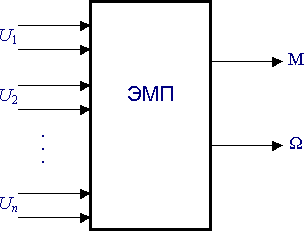
Рис. 2.1. Электромеханический многополюсник

Для построения математического описания динамических процессов в электродвигательных устройствах любого типа (постоянного и переменного тока) используются элементы теории обобщенной электрической машины [2]. Без ее использования практически невозможно построить модель электродвигателей переменного тока.

Известно [2], что любая многофазная электрическая машина с n–фазной обмоткой статора и m–фазной обмоткой ротора при условии равенства полных сопротивлений фаз статора (ротора) для изучения динамических процессов может быть представлена эквивалентной двухфазной машиной.

Понятие обобщенной электрической машины

Обобщенная машина является упрощенной моделью реальной машины. Ее отличительными признаками являются:

Сосредоточенные в пазах проводники стоком заменены синусоидальными токовыми слоями, эквивалентными по магнитодинамической силе (МДС) первым гармоникам МДС соответствующих реальных обмоток.

Не учитывается неравномерность воздушного зазора, обусловленная пазами.

Наличие явнополюсной структуры на статоре (роторе) учитывается введением первой гармоники переменной составляющей зазора.

Магнитная цепь имеет очень высокую магнитную проницаемость и не насыщается, то есть считается, что энергия магнитного поля сосредоточена в воздушном зазоре. Влияние явнополюсности учитывается введением переменной радиальной магнитной проницаемости [2]

— соответственно электрической и геометрический угол поворота ротора относительно статора; 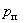— число пар полюсов машины.

Полные сопротивления фаз статора и ротора равны.

Математическое описание процессов электромеханического преобразования энергии в обобщенной машине

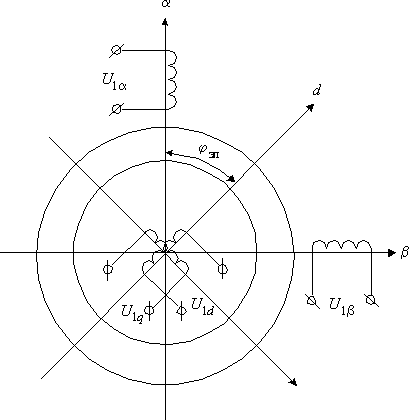
Обобщенная электрическая машина может быть представлена схемой приведенной на рис. 2.2. Две обмотки статора размещены в ортогональной системе координат 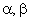, неподвижной относительно статора, а две обмотки ротора – в ортогональной системе координат d, q, неподвижной относительно ротора.

Рис. 2.2. Схема обобщенной машины

Для координат и параметров обобщенной машины будем использовать следующую систему индексов. Индексами 1 и 2 будем обозначать координаты и параметры, относящиеся соответственно к статору и ротору; индексы 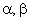, d, q определяют принадлежность координат к соответствующей оси машины.

Динамика обобщенной электрической машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии. Уравнения электрического равновесия, выраженные через потокосцепления, и записанные относительно реальных напряжений и токов статора и ротора

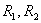
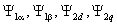
где – активное сопротивление одной фазы статора (ротора), — потокосцепления соответствующих индексам обмоток.

Уравнения (2.2) однотипны и их можно записать в компактной обобщающей форме:

где индекс i принимает значения 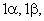2d, 2q, соответствующие индексам обмоток.

Потокосцепления обмоток в общем виде определяются результирующим действием токов всех обмоток машины:

Однотипность записи уравнений (2.4) позволяет в дальнейшем прибегнуть к удобной обобщенной форме записи этой системы

При работе машины взаимное положение обмоток статора и ротора изменяется, поэтому собственные и взаимные индуктивности обмоток в общем случае являются функцией угла поворота ротора

.

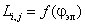
Для симметричной неянополюсной машины собственные индуктивности статора и ротора не зависят от положения ротора

,

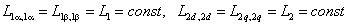
а взаимные индуктивности между обмотками статора или ротора равны нулю

,

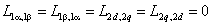
так как магнитные оси этих обмоток сдвинуты в пространстве на угол

.

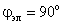
Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменений при повороте ротора на угол

,

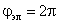
поэтому можно записать

С учетом выражения (2.5) уравнения электрического равновесия можно представить в обобщенной форме записи

где 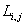определяются формулами (2.6).

В результате взаимодействия токов, протекающих по обмоткам обобщенной машины, на ее роторе создается электромагнитный момент М, который может быть определен с помощью известных соотношений [2]:

С помощью выражения (2.5) электромагнитный момент может быть выражен через токи обмоток:

Уравнения электрического равновесия (2.7) в сочетании с уравнением электромагнитного момента (2.8) представляют собой математическое описание динамического процесса преобразования энергии, которое в дальнейшем будет конкретизировано для наиболее используемых разновидностей электродвигателей. В обобщенной форме это описание принимает следующий вид:

Уравнение электромагнитного момента можно упростить, подставив в (2.9) выражения для собственных и взаимных индуктивностей обмоток (2.6):

В электрическом двигателе осуществляется связь механического движения привода и приводимого им в движение механизма с электрическими процессами в системе автоматического управления и наоборот. Эта связь объединяет механическую и электрическую части в единую электромеханическую систему.

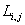
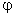
Так как зависят от угла , а, следовательно, и от времени t, уравнение (2.7) после дифференцирования по времени преобразуется к виду:

— угловая скорость вала двигателя.

Первый член каждого уравнения (2.12) представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй – результирующую ЭДС самоиндукции и взаимной индукции 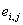, вызванную изменениями токов в обмотках, а третий член отражает взаимодействие механической и электрической частей электропривода и представляет собой результирующую ЭДС, наведенную в обмотке в результате механического движения ротора машины.

Следовательно, математическое описание процессов преобразования энергии в обобщенной электрической машине в общем виде имеет следующий вид:

Контрольные вопросы к лекции No 2.

Назовите основное условие возможности представления многофазной электрической машины с n–фазной обмоткой статора и m–фазной обмоткой ротора эквивалентной двухфазной машиной.

С какой скорость вращаются обмотки статора обобщенной электрической машины?

С какой скорость вращаются обмотки ротора обобщенной электрической машины?

Значения каких индуктивностей обмоток статора и ротора от угла поворота ротора ?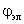

Поясните физический смысл полученных уравнений электрического равновесия напряжений в обмотках обобщенной электрической машины:

.

Полные сопротивления фаз статора и ротора должны быть соответственно равны.

Обмотки статора обобщенной электрической машины неподвижны в пространстве.

Обмотки ротора обобщенной электрической машины неподвижны относительно ротора и вращаются в пространстве со скоростью ротора.

Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменений при повороте ротора на угол.

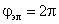
Первый член каждого уравнения представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй – результирующую ЭДС самоиндукции и взаимной индукции , вызванную изменениями токов в обмотках, а третий член отражает взаимодействие механической и электрической частей электропривода и представляет собой результирующую ЭДС, наведенную в обмотке в результате механического движения ротора машины.

Источник

Понятие обобщенной электрической машины

Обобщенная машина является упрощенной моделью реальной машины. Ее отличительными признаками являются:

1. Сосредоточенные в пазах проводники стоком заменены синусоидальными токовыми слоями, эквивалентными по магнитодинамической силе (МДС) первым гармоникам МДС соответствующих реальных обмоток.

2. Не учитывается неравномерность воздушного зазора, обусловленная пазами.

3. Наличие явнополюсной структуры на статоре (роторе) учитывается введением первой гармоники переменной составляющей зазора.

4. Магнитная цепь имеет очень высокую магнитную проницаемость и не насыщается, то есть считается, что энергия магнитного поля сосредоточена в воздушном зазоре. Влияние явнополюсности учитывается введением переменной радиальной магнитной проницаемости [2]

(2.1)

Где

— соответственно электрической и геометрический угол поворота ротора относительно статора; — число пар полюсов машины.

5. Полные сопротивления фаз статора и ротора равны.

Математическое описание процессов электромеханического преобразования энергии в обобщенной машине

Обобщенная электрическая машина может быть представлена схемой приведенной на рис. 2.2. Две обмотки статора размещены в ортогональной системе координат , неподвижной относительно статора, а две обмотки ротора – в ортогональной системе координат d, q, неподвижной относительно ротора.

Рис. 2.2. Схема обобщенной машины

Для координат и параметров обобщенной машины будем использовать следующую систему индексов. Индексами 1 и 2 будем обозначать координаты и параметры, относящиеся соответственно к статору и ротору; индексы , d, q определяют принадлежность координат к соответствующей оси машины.

Динамика обобщенной электрической машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии. Уравнения электрического равновесия, выраженные через потокосцепления, и записанные относительно реальных напряжений и токов статора и ротора

имеют вид:

где – активное сопротивление одной фазы статора (ротора), — потокосцепления соответствующих индексам обмоток.

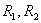
Уравнения (2.2) однотипны и их можно записать в компактной обобщающей форме: где индекс i принимает значения 2d, 2q, соответствующие индексам обмоток.

Потокосцепления обмоток в общем виде определяются результирующим действием токов всех обмоток машины:

Однотипность записи уравнений (2.4) позволяет в дальнейшем прибегнуть к удобной обобщенной форме записи этой системы

При работе машины взаимное положение обмоток статора и ротора изменяется, поэтому собственные и взаимные индуктивности обмоток в общем случае являются функцией угла поворота ротора 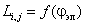. Для симметричной неянополюсной машины собственные индуктивности статора и ротора не зависят от положения ротора , а взаимные индуктивности между обмотками статора или ротора равны нулю , так как магнитные оси этих обмоток сдвинуты в пространстве на угол

Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменений при повороте ротора на угол ,

поэтому можно записать

С учетом выражения (2.5) уравнения электрического равновесия можно представить в обобщенной форме записи где определяются формулами (2.6).

В результате взаимодействия токов, протекающих по обмоткам обобщенной машины, на ее роторе создается электромагнитный момент М, который может быть определен с помощью известных соотношений [2]:

С помощью выражения (2.5) электромагнитный момент может быть выражен через токи обмоток:

Уравнения электрического равновесия (2.7) в сочетании с уравнением электромагнитного момента (2.8) представляют собой математическое описание динамического процесса преобразования энергии, которое в дальнейшем будет конкретизировано для наиболее используемых разновидностей электродвигателей. В обобщенной форме это описание принимает следующий вид: Уравнение электромагнитного момента можно упростить, подставив в (2.9) выражения для собственных и взаимных индуктивностей обмоток (2.6):

В электрическом двигателе осуществляется связь механического движения привода и приводимого им в движение механизма с электрическими процессами в системе автоматического управления и наоборот. Эта связь объединяет механическую и электрическую части в единую электромеханическую систему.

Так как зависят от угла , а, следовательно, и от времени t, уравнение (2.7) после дифференцирования по времени преобразуется к виду: где — угловая скорость вала двигателя.

Первый член каждого уравнения (2.12) представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй – результирующую ЭДС самоиндукции и взаимной индукции , вызванную изменениями токов в обмотках, а третий член отражает взаимодействие механической и электрической частей электропривода и представляет собой результирующую ЭДС, наведенную в обмотке в результате механического движения ротора машины.

Следовательно, математическое описание процессов преобразования энергии в обобщенной электрической машине в общем виде имеет следующий вид:

Источник

Электромеханический преобразователь и обобщённая электрическая машина

Электромеханический преобразователь(в дальнейшем ЭМП) –идеальный Эл. двигатель, имеющий идеальный ротор, не имеющий потерь и жёстко взаимодействующий с реальным ротором.

ЭМП оперирует с переменным током. Обычно рассматривают 2-х фазную электрическую машину.

Оси α, β –оси неподвижного статора.

Оси d, q –оси неподвижного ротора.

При протекании токов через все катушки возникает потокосцепление как в самих катушках, так и потокосцепление любой из катушек со всеми остальными.

Уравнение электрического равновесия

Идеальная машина: индукция не имеет насыщения; μ→∞ и полное сопротивление катушек статора и ротора идентичны.

; ; ;

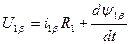
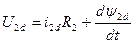
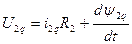
Общее потокосцепление: ;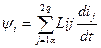

Индекс появления токов в соответствующей обмотке: i=1α, 1β, 2d, 2q;

Индекс обмотки, влияющей на появления тока: j=1α, 1β, 2d, 2q;

L_1α,1β·i_1β –потокосцепление, появляется противоэ.д.с. в обмотке 1α под влиянием тока 1β.

Потокосцепление первой катушки:

Самоиндукции:; ;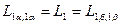

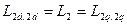
Взаимоиндукция:

Рассмотрим взаимоиндукцию:; ;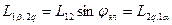

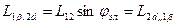
В результате преобразований, уравнения электрического равновесия записывается: 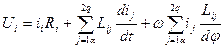dφ=ωdt

где U_i – напряжение на i-той обмотке;

i_iR_i – падения напряжения на активной составляющей i-той обмотки;

В этом случае данное уравнение отражает электромеханическую связь, объединяющую механическую составляющую электропривода и ЭМП в единую систему. Т.е. электромагнитный момент изменяется под действием изменяющегося Mс и следовательно под действием меняющихся токов в обмотках он же влияет на механическую часть привода.

Достоинство электромеханического преобразователя (в дальнейшем ЭМП) в идеальном двигателе в том, что здесь оперируют с действующими значениями токов и напряжений. Однако большое количество взаимосвязей между индуктивностями и взаимодействие всех четырех обмоток приведет к усложнению расчетов.

Для упрощения этих расчетов и исключения зависимости L_ij от φ_эл. и перехода использования амплитудных значений токов и напряжений осуществляется векторное преобразования координат:

Сущность преобразования в том, что на ряду с координатами α и β статора и d и q ротора, вводятся дополнительно координаты U и V, которые вращается относительно неподвижных координат статора на φ_к.

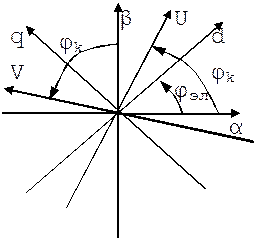
В этом случае для преобразования координат и получения новых значений векторов производится суммирование проекций векторов.

результирующая проекций напряжений X_1α и X_1β.

Какая-либо величина напряжения или тока изображается в виде вектора проекций X_1α и X_1β. Затем эти проекции проецируются на вращающиеся оси V и U. И определяется результирующая X₁ вектора.

В этом случае для преобразования координат и получения новых значений векторов токов производится суммирование проекций векторов.

результирующая проекций напряжений X_1α и X_1β.

Какая-либо величина напряжения или тока изображается в виде вектора относящихся к статору и проектируется в виде проекций X_1α и X_1β. Затем эти проекции проектируются на вращающиеся оси V и U, и определяется результирующая X₁ , этого вектора относительно U и V. В результате такого преобразования получается, что катушки статора и ротора получаются следующие.

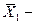
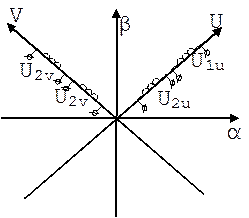
Достоинство: исключается взаимное влияние Кат. 1U, 2U с кат. 1V, 2V

Т.е. в катушках на одной оси существует самоиндукция и взаимоиндукция и только.

Тогда уравнение электрического равновесия,

;

для ротора:; ;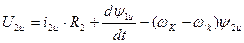

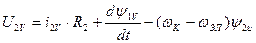
Электромагнитный момент:

p_n – количество пар полюсов; L₁₂ – взаимоиндуктивность между статором и ротором; i_i – токи в обмотках.

Если рассмотреть эти соотношения с позиции электропривода, то они обладают нелинейностью. Чтобы упростить расчеты используют понятия “разложение нелинейности вокруг положения равновесии”.

общее дифференциальное уравнение вида:

a(p), b(p), c(p) – полиномы представляющие собой некоторые значения; ω(p) – возмущение воздействия; u(p) – управляющее воздействие; M(p) – регулируемая величина.

Эту систему с позиции управления:

Структурная схема для данного уравнения:

Рассмотрим эти системы с позиции возмущения:

Частота холостого хода:

Электромагнитный момент:

Структурная схема для данного уравнения:

Передаточная функция электромеханического преобразователя по возмущению называется динамической жесткостью механические характеристики:;

Т.е., используя частотные свойства, можно найти зависимость осуществления колебательного процесса в системе при изменении момента сопротивления.

Источник