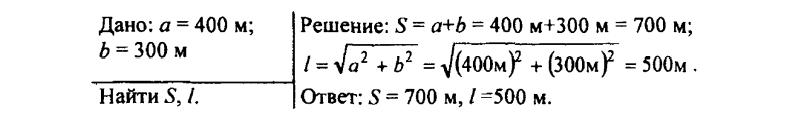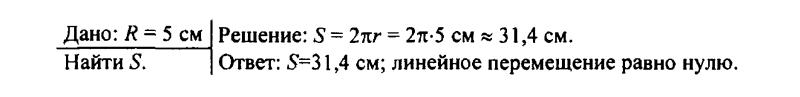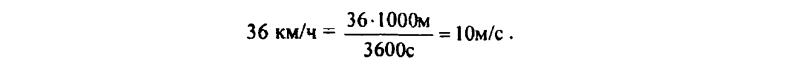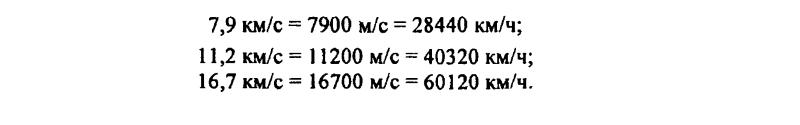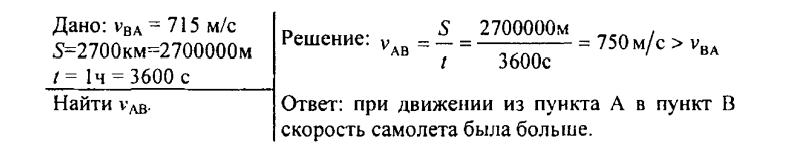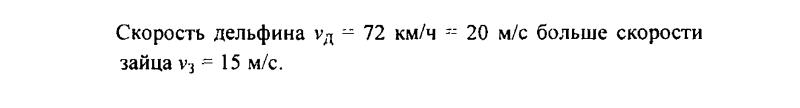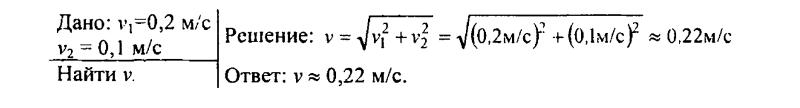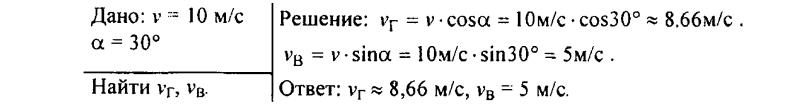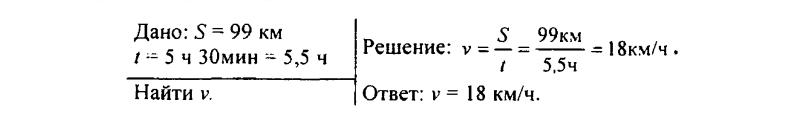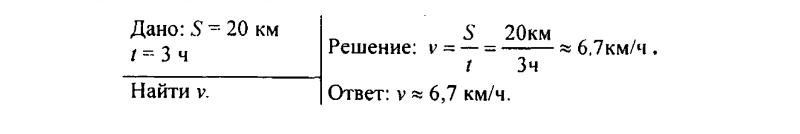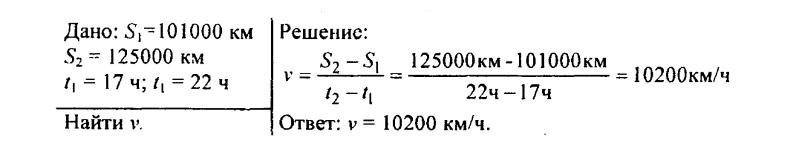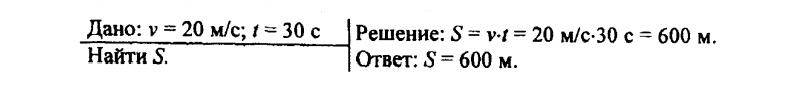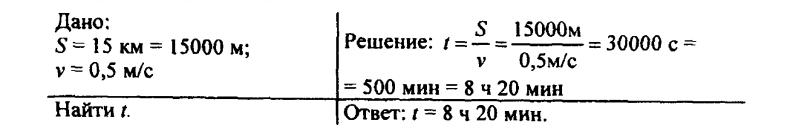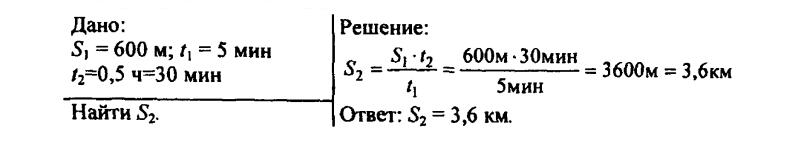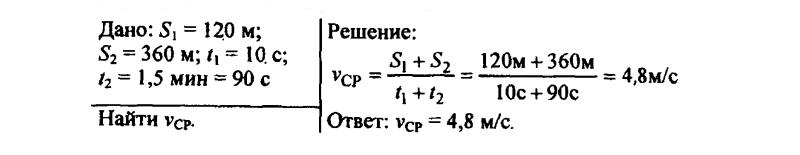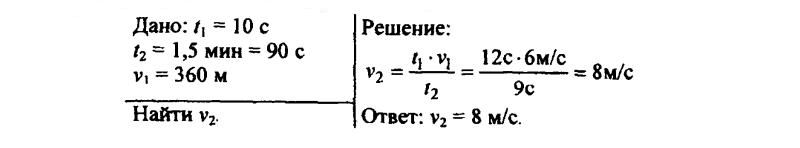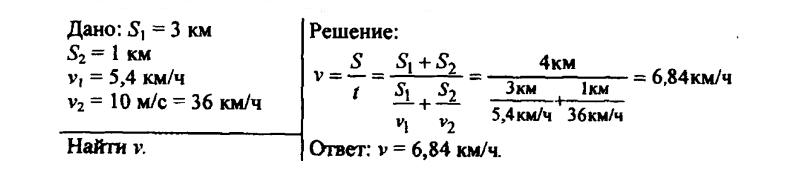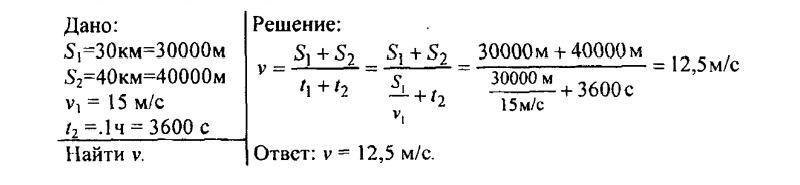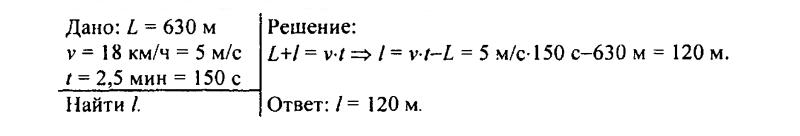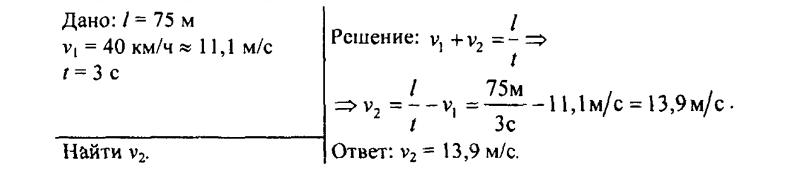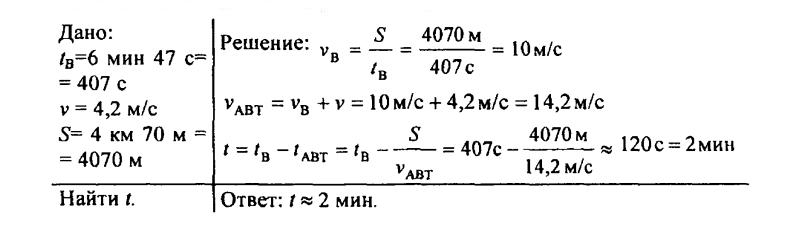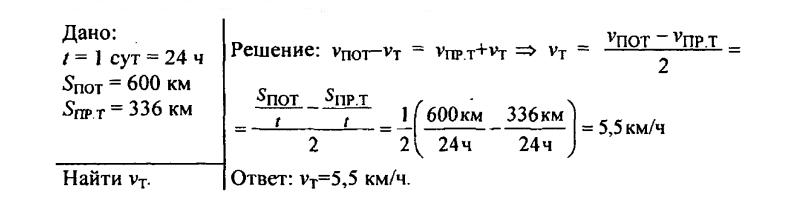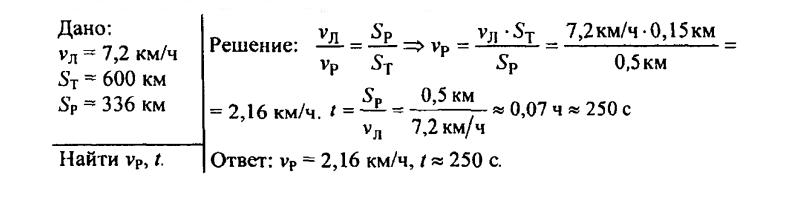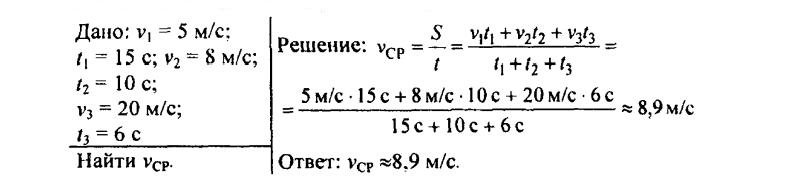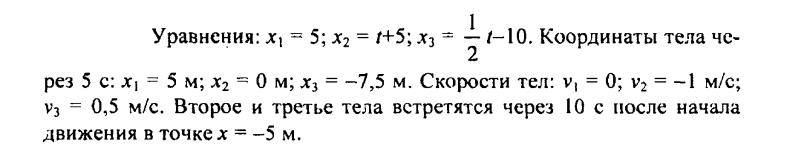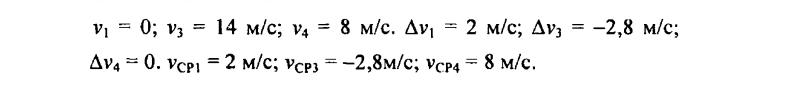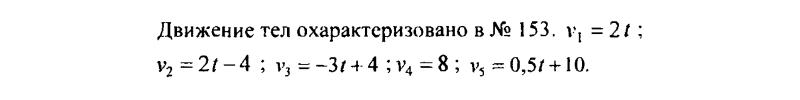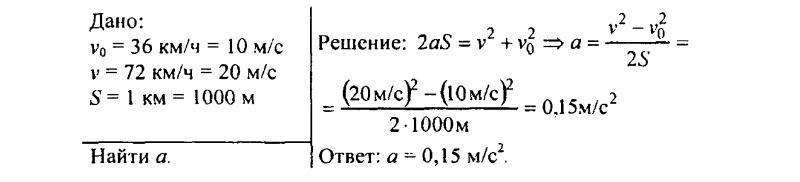Один автомобиль проехал пункт а со скоростью 40 км ч двигаясь равномерно второй автомобиль

Задачи на движение

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

Примеры простых задач.

Задача 1.

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2.

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3.

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4.

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5.

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6.

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7.

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8.

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9.

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10.

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11.

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Итак, для решения задач на движение:

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.

Источник

Первую половину пути автомобиль двигается со скоростью 60 км/ч, а вторую

Условие задачи:

Первую половину пути автомобиль двигается со скоростью 60 км/ч, а вторую – со скоростью 40 км/ч. Определить среднюю скорость движения автомобиля на всем пути.

Задача №1.2.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

\(S_1=S_2=\frac<1><2>S\), \(\upsilon_1=60\) км/ч, \(\upsilon_2=40\) км/ч, \(\upsilon_<ср>-?\)

Решение задачи:

Так как и на первом, и на втором участке автомобиль двигался равномерно, то справедливо записать такую систему.

Выразим из каждого выражения время.

Подставим эти выражения в формулу средней скорости.

По условию \(S_1=S_2=\frac<1><2>S\), поэтому:

Подставив в эту итоговую формулу исходные данные задачи, мы получим ответ. Переводить значения скоростей в систему СИ не имеет смысла, подставив их без изменений в формулу, мы получим ответ так же в км/ч.

Ответ: 13,3 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

Помогите пожалуйста с задачей авто двигалось 2 часа первый час 90 км в час а второй 60. Найдите среднюю скорость авто на первой половине пути и на второй

Задача устная. Всего за два часа авто пройдет 150 км (за первый час 90 км, а за второй – 60 км), значит половина пути равна 75 км. Так как первый час авто движется равномерно со скоростью 90 км/ч и проходит 90 км, значит средняя скорость на первой половине пути (поскольку 75 км Ответить

Извините, а вы не подскажите как решить? В течение первой секунды от начала движения ускорение грузовика было 6,0 м/с², в каждую последующую секунду ускорение убывало на 60%. Какова средняя скорость автомобиля за первые 8 с движения?

Источник

Один автомобиль проехал пункт а со скоростью 40 км ч двигаясь равномерно второй автомобиль

Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 17 км/ч, а вторую половину пути — со скоростью 102 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она меньше 60 км/ч. Ответ дайте в км/ч.

Это задание ещё не решено, приводим решение прототипа.

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.

Пусть км/ч – скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:

Таким образом, скорость первого автомобиля была равна 52 км/ч.

По условию, оба автомобиля проехали одинаковое расстояние за одно и то же время, а значит, средние скорости их движения равны. Поэтому из приведенного решения следует, что средняя скорость второго автомобиля равна 52 км/ч, его скорость на первой половине пути составляет 52 − 13 = 39 км/ч, а скорость на второй половине пути — 78 км/ч. Невнимательный читатель мог бы решить, что в решении ошибка, поскольку Однако противоречия нет.

Первую половину пути автомобиль ехал с меньшей скоростью, значит, он затратил на первую половину пути больше времени, чем на вторую. Поэтому среднюю скорость нельзя находить по формуле Пусть половина пути между пунктами А и В равна х км, тогда для прохождения первой половины пути второму автомобилю потребовалось часов, для прохождения второй половины пути часов, а всего часов. Тогда средняя скорость второго автомобиля составит

км/ч,

то есть действительно будет равна скорости первого автомобиля.

Источник

Один автомобиль проехал пункт а со скоростью 40 км ч двигаясь равномерно второй автомобиль

Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.

1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.

2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.

3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.

5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.

Переведем скорость

Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.

1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).

2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.

3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно Значит, Р = 15 кН.

4. Верно. (см. пункт 3).

5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).

Источник

95. В движущемся вагоне пассажирского поезда на столе лежит книга. В покое или движении находится книга относительно: а) стола; б) рельсов; в) пола вагона; г) телеграфных столбов?
Книга находится в покое относительно стола и пола вагона, в движении относительно рельсов и телеграфных столбов.

96. Какую траекторию при движении описывает центр колеса автомобиля относительно прямолинейной дороги?
Прямую линию.

97. Рассмотрите движение концов минутной и часовой стрелок часов. Что между этими движениями общего? Чем они отличаются друг от друга?
Эти движения имеют разную скорость и траекторию одного вида.

98. Велосипедист движется равномерно и прямолинейно. Какова траектория движения точек обода колеса относительно рамы велосипеда?
Окружность.

99. Какие части велосипеда при прямолинейном движении описывают прямолинейные траектории относительно дороги, а какие — криволинейные?
Прямолинейную траекторию описывает рама, криволинейную траекторию описывает точка на ободе.

100. После стыковки космический корабль и орбитальная станция двигались некоторое время совместно. Что можно сказать о скорости и виде их движения относительно друг друга и относительно Земли при таком полете?
Их скорость была равна нулю.

101. На рисунке 19 изображена часть траектории движения Земли вокруг Солнца. Стрелками показаны направления движения Земли и ее вращения. Когда жители Москвы движутся в пространстве быстрее относительно Солнца: в полдень или в полночь? Почему?
В полдень, т.к. к скорости движения Земли прибавляется скорость ее вращения, и скорость жителя Москвы относительно Солнца становится больше.

102. Группа самолетов (рис. 20) одновременно выполняет фигуры высшего пилотажа, сохраняя заданный строй. Что можно сказать о движении самолетов относительно друг друга?
Их скорость относительно друг друга равна нулю.

103. Шарик в трубке с водой (рис. 21) равномерно опускается за каждую секунду на 5 см. В каком направлении и с какой скоростью следует перемещать трубку, чтобы шарик относительно поверхности Земли оставался в состоянии покоя?
Трубку следует перемещать вертикально вверх со скоростью v=5 см/с.

104. Велосипедист проехал путь от А до Б (рис. 22). Одинаковые ли пути пройдены при этом передним и задним колесами велосипеда?
Одинаковы.

105. Одинаковые ли пути проходят правые и левые колеса автомобиля при повороте (рис. 23)?
Нет, меньшее расстояние проходят колеса, в сторону кото¬рых происходит поворот.

106. Определите знаки проекций векторов перемещения s1,s2, s3, s4, s5, s6 на оси координат X и Y (рис. 24).

107. Кабина лифта опустилась с одиннадцатого этажа здания на пятый, а затем поднялась на восьмой этаж. Считая, что расстояния между этажами равны по 4 м, определите путь и перемещение кабины.
Какой знак имеет проекция вектора перемещения на ось, направленную вертикально вверх?
Путь: 36 м. Перемещение (имеет отрицательную проекцию на вертикальную ось, направленную вверх): 12 м.

108. Автомобиль проехал по улице путь, равный 400 м, затем свернул направо и проехал по переулку еще 300 м. Считая движение прямолинейным на каждом из отрезков пути, найдите путь автомобиля и его перемещение.

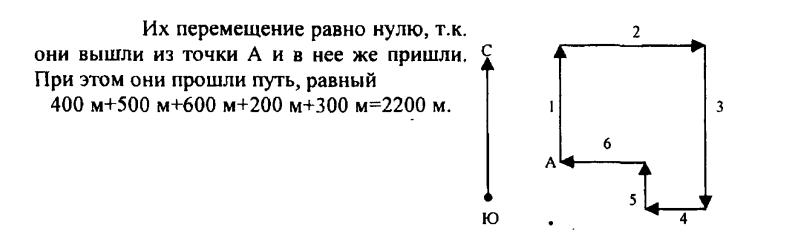
109. В военно-патриотической игре группа школьников получила задание пройти путь, равный 400 м на север, 500 м на восток, 600 м на юг, 200 м на запад, 200 м на север и 300 м на запад. Изобразите траекторию передвижения группы и определите весь пройденный ею путь и перемещение.

110. Минутная стрелка часов за один час совершает полный оборот. Какой путь проходит при этом конец стрелки длиной 5 см? Чему равно линейное перемещение конца стрелки?

111. Каждый из участков пути АВ, ВС и CD автомобиль проезжает за 1 мин (рис. 25). На каком участке скорость наибольшая, на каком — наименьшая?
На ВС — скорость наименьшая; на DC — скорость наибольшая.

112. На рисунке 26 обозначена траектория движения искусственного спутника Земли. Участки траектории бе и га спутник проходит за одинаковое время. На каком из участков средняя скорость спутника больше?
Средняя скорость спутника больше на участке вг.

113. Домик полярников с дрейфующей льдиной за первые сутки переместился на 5 км, за вторые сутки — на 5 км, за третьи — на 5 км и т. д. Можно ли считать такое движение равномерным?
Можно, но только в том случае, если перемещение совершалось вдоль прямой линии в одном направлении. Вероятность такого движения льдины крайне мала, так что, скорее всего, такое движение нельзя считать равномерным.

114. Автомобиль равномерно движется с запада на восток со скоростью 60 км/ч. Изобразите графически скорость автомобиля (масштаб: 0,5 см — 10 км/ч).

115. Шарик тонет в воде. Каждую секунду он проходит путь, равный 10 см. Изобразите графически скорость движения шарика (масштаб: 2 см — 10 см/с).

116. С востока на запад при встречном ветре, скорость которого 6 м/с, движется велосипедист со скоростью 8 м/с. Изобразите графически (стрелкой) эти скорости (масштаб: 0,5 см — 2 м/с).

117. Муха летит со скоростью 18 км/ч. Выразите эту скорость в сантиметрах в секунду (см/с); метрах в секунду (м/с). Последнюю скорость изобразите графически (стрелкой), полагая, что муха летит в направлении с востока на запад (масштаб: 1м/с — 0,5 см).

118. Трамвай движется со скоростью 36 км/ч. Выразите эту скорость в метрах в секунду (м/с).

119. Известно, что первая, вторая и третья космические скорости соответственно равны 7,9 км/с, 11,2 км/с, 16,7 км/с. Выразите эти скорости в метрах в секунду (м/с) и в километрах в час (км/ч).

120. От пункта А до пункта В путь, равный 2700 км, реактивный самолет пролетел за 1 ч. Обратный путь он летел со скоростью 715 м/с. В каком направлении скорость самолета была больше?

121. Скорость зайца равна 15 м/с, а скорость дельфина — 72 км/ч. Кто из них имеет большую скорость?

122. Скорость v1 вертикального подъема груза краном равна 0,2 м/с. Скорость v2 тележки крана равна 0,1 м/с (рис. 27). Определите скорость движения груза относительно наблюдателя, неподвижно стоящего на поверхности Земли.

123. Санки скатываются с горы и в некоторый момент времени имеют скорость 10 м/с. Чему равны горизонтальная составляющая vг и вертикальная составляющая vг этой скорости в данный момент, если наклон горы равен 30° к горизонту?

124. За 5 ч 30 мин велосипедист проделал путь 99 км. С какой средней скоростью двигался велосипедист?

125. Вычислите среднюю скорость лыжника, прошедшего путь 20 км за 3 ч.

126. Вычислите скорость движения пешехода, кавалериста, танка (Т-34), пассажирского самолета (Ил-62), если путь 20 км они проходят соответственно за 5 ч; 2 ч; 22 мин; 1,4 мин.

127. К 17 ч 12 сентября 1959 г. вторая космическая ракета, доставившая советский вымпел на Луну, удалилась от поверхности Земли на расстояние 101 000 км. К 22 ч того же дня она находилась уже на расстоянии 152 000 км от Земли. Определите среднюю скорость удаления ракеты от Земли.

128. В течение 30 с поезд двигался равномерно со скоростью 72 км/ч. Какой путь прошел поезд за это время?

129. Юный пассажир в самолете дальнего следования отметил, что полет над лесом длился ровно 1 мин. Зная скорость полета самолета (850 км/ч), он тут же определил длину пути, пройденного самолетом над лесом. Какой результат получил юный пассажир?

130. За сколько времени плывущий по течению реки плот пройдет 15 км, если скорость течения 0,5 м/с?

131. В подрывной технике употребляют сгорающий с небольшой скоростью бикфордов шнур. Какой длины надо взять шнур, чтобы успеть отбежать на расстояние 300 м, после того как его зажгут? Скорость бега равна 5 м/с, а пламя по шнуру распространяется со скоростью 0,8 см/с.

132. Трактор за первые 5 мин проехал 600 м. Какой путь он пройдет за 0,5 ч, двигаясь с той же скоростью?

133. Вагон, двигаясь под уклон с сортировочной горки, проходит 120 м за 10 с. Скатившись с горки и продолжая двигаться, он проходит до полной остановки еще 360 м за 1,5 мин. Определите среднюю скорость вагона за все время движения.

134. Один велосипедист 12 с двигался со скоростью 6 м/с, а второй проехал этот же участок пути за 9 с. Какова средняя скорость второго велосипедиста на этом участке пути?

135. Поднимаясь в гору, лыжник проходит путь, равный 3 км, со средней скоростью 5,4 км/ч. Спускаясь с горы со скоростью 10 м/с, он проходит 1 км пути. Определите среднюю скорость лыжника на всем пути.

136. Автомобиль первую часть пути (30 км) прошел со средней скоростью 15 м/с. Остальную часть пути (40 км) он прошел за 1 ч. С какой средней скоростью двигался автомобиль на всем пути?

137. Автобус первые 4 км пути проехал за 12 мин, а следующие 12 км — за 18 мин. Какова средняя скорость автобуса на каждом участке пути и на всем пути?

138. Определите длину поезда, движущегося равномерно по мосту длиной 630 м со скоростью 18 км/ч, если поезд проходит мост в течение 2,5 мин.

139. Пассажир поезда, идущего со скоростью 40 км/ч, видит в течение 3 с встречный поезд длиной 75 м. С какой скоростью движется встречный поезд?

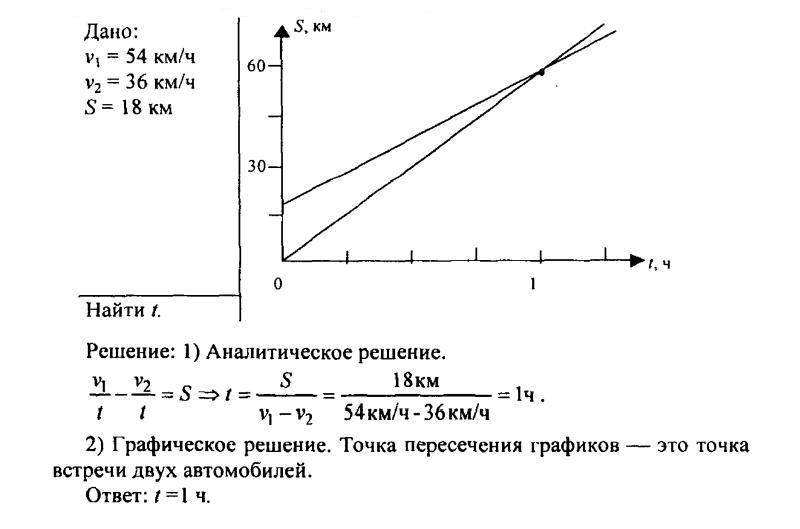
140. Два автомобиля движутся прямолинейно и равномерно в одном направлении со следующими скоростями: v1=54 км/ч и v2=36 км/ч. В начале наблюдения расстояние между ними было равно 18 км. Через какое время первый автомобиль догонит идущий впереди второй автомобиль? Решите задачу аналитически и графически.

141. Венеция соединена с материковой частью Италии мостом длиной 4 км 70 м. Велосипедист преодолевает это расстояние за время, которое равно 6 мин 47 с. Определите, на сколько минут позже должен въехать на мост автомобиль, чтобы догнать велосипедиста в конце моста, если скорость автомобиля больше на 4,2 м/с скорости велосипедиста.

142. Из пунктов А и Б по шоссе навстречу друг другу движутся два автобуса. Один выехал в 9 ч из пункта А, а другой — в 9 ч 30 мин из пункта Б. Первый движется со скоростью 40 км/ч, а второй — со скоростью 60 км/ч. Расстояние между пунктами равно 120 км. В какое время и на каком расстоянии от пункта А автобусы встретятся?

143. Определите скорость течения реки, если грузовой теплоход проходит за сутки по течению путь, равный 600 км, и против течения путь, равный 336 км, за то же время.

144. Лодка держит курс перпендикулярно берегу и движется со скоростью 7,2 км/ч. Течение относит ее на расстояние 150 м вниз по реке. Найдите скорость течения реки и время, затраченное на переезд через реку. Ширина реки равна 0,5 км.

145. Мотоцикл двигался в течение 15 с со скоростью 5 м/с, в течение 10 с со скоростью 8 м/с и в течение 6 со скоростью 20 м/с. Какова средняя скорость движения мотоцикла?

146. Три четверти своего пути автомобиль прошел со скоростью 60 км/ч, остальную часть пути — со скоростью 80 км/ч. Какова средняя скорость движения автомобиля?

147. На рисунке 28 представлены графики зависимости пути от времени для трех тел. Какое из этих тел движется равномерно? Можно ли утверждать, что тела движутся прямолинейно?
Равномерно движется тело №1.0 характере траектории мы ничего не можем сказать.

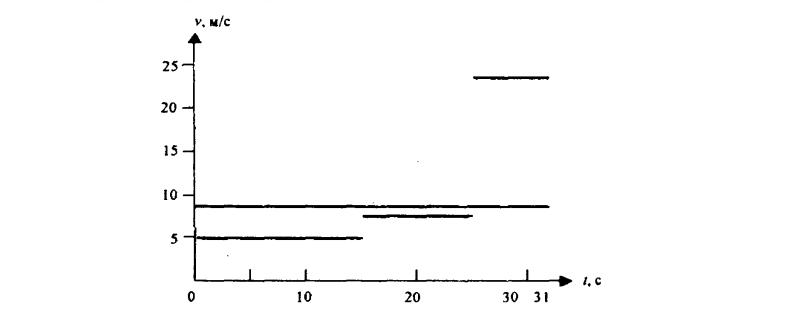
148. По графику зависимости пути от времени (рис. 29) определите значения скорости на каждом этапе пути и среднюю скорость тела за время движения. Можно ли утверждать, что в моменты времени, соответствующие изломам графика, тело движется равномерно?

149. По данным условия задачи 145 постройте график скорости и определите отрезки пути, пройденные телом на каждом этапе движения. Постройте график средней скорости движения тела. Сравните площади под графиками.
Площади под графиком скорости и графиком средней скорости равны.

150. На рисунке 30 представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

151. По графикам (рис. 31) напишите уравнения движения х = х (t). Из уравнений и графиков найдите координаты тел через 5 с, скорости движения тел, время и место встречи второго и третьего тел.

152. Тело, двигаясь без начальной скорости, прошло за первую секунду путь, равный 1 м, за вторую секунду путь, равный 2 м, за третью секунду 3 м, за четвертую секунду 4 м и т. д. Можно ли считать такое движение равномерным?
Нельзя.

153. Какой из графиков на рисунке 32 соответствует равномерному прямолинейному движению, а какой — равноускоренному? Можно ли однозначно утверждать, что точка пересечения графиков 3 и 5 свидетельствует о том, что в данный момент времени координаты тел совпадают?
Равномерному прямолинейному движению соответствует график 4; равноускоренному — графики 1, 2, 5; равнозамедленному график 3. То, что графики 3 и 5 пересекаются, не позволяет однозначно утверждать, что координаты тел совпадают.

154. По данным графиков 1, 3, 4 (рис. 32) определите начальную скорость, приращение скорости за одну секунду, среднюю скорость движения за шесть секунд.

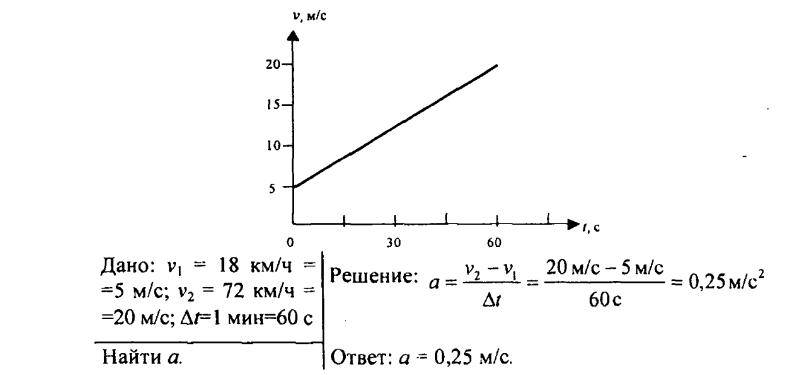
155. С каким средним ускорением двигался автобус, если за время, равное 1 мин, показания скорости на спидометре изменились от 18 до 72 км/ч? Постройте график зависимости скорости от времени.

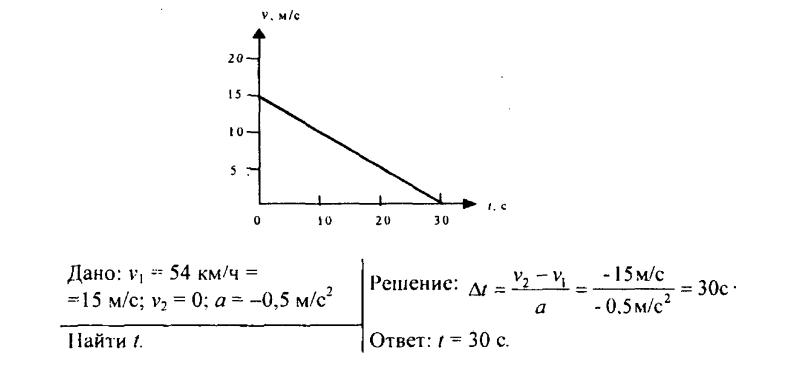
156. Вагон движется равноускоренно с ускорением 0,5 м/с2. Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

157. Пользуясь графиками рисунка 32, поясните, как двигались тела. Запишите формулу зависимости скорости от времени для каждого из тел.

158. С каким ускорением двигался автомобиль, если на пути 1 км его скорость возросла от 36 до 72 км/ч?

159. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

160. Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с2. Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(f).

Источник