Ограниченная машина больцмана это

Моделирование нейросети Машина Больцмана

Уважаемое хабросообщество, решил поделиться с вами моими наработками в изучении нейросети Машины Больцмана, сделанными в студенческие года.

В России по данной теме было крайне мало информации. Даже руководитель нашей кафедры не мог мне помочь с материалом. Благо наш университет состоял в единой международной базе, и была возможность воспользоваться зарубежным опытом. В частности, большая часть была найдена в литературе оксфордского университета. По сути, данная статья является сборником информации из различных источников, переосмысленная и изложенная достаточно понятным языком, как мне кажется. Надеюсь кому-то будет интересно. Когда-то меня это заставляло не спать ночами.
Итак, приступим.

Сеть Хопфилда

Среди различных конфигураций искуственных нейронных сетей (НС) встречаются такие, при классификации которых по принципу обучения, строго говоря, не подходят ни обучение с учителем [1], ни обучение без учителя [2]. В таких сетях весовые коэффициенты синапсов рассчитываются только однажды перед началом функционирования сети на основе информации об обрабатываемых данных, и все обучение сети сводится именно к этому расчету. С одной стороны, предъявление априорной информации можно расценивать, как помощь учителя, но с другой – сеть фактически просто запоминает образцы до того, как на ее вход поступают реальные данные, и не может изменять свое поведение, поэтому говорить о звене обратной связи с «миром» (учителем) не приходится. Из сетей с подобной логикой работы наиболее известны сеть Хопфилда, которая обычно используются для организации ассоциативной памяти. Именно ее мы и рассмотрим.
Структурная схема сети Хопфилда приведена на рисунке ниже. Она состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон связан синапсами со всеми остальными нейронами, а также имеет один входной синапс, через который осуществляется ввод сигнала. Выходные сигналы, как обычно, образуются на аксонах.

На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом [3][4]:
(1)
Здесь i и j – индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk – i-ый и j-ый элементы вектора k-ого образца.
Алгоритм функционирования сети следующий (p – номер итерации):
1. На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений аксонов:
Yi(0) = xi, i = 0. n-1 (2)
поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от yi означает нулевую итерацию в цикле работы сети.
2. Рассчитывается новое состояние нейронов
(3)
и новые значения аксонов
(4)

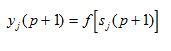
Рис. 4 Активационные функции
где f – активационная функция в виде скачка, приведенная на рисунке (4)

3. Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.
Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов m не должно превышать величины, примерно равной 0.15•n. Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.
Так же для полного понимания функционирования сети необходимо упомянуть о правиле Хебба.
Правило обучения для сети Хопфилда опирается на исследования Дональда Хебба (D.Hebb, 1949), который предположил, что синаптическая связь, соединяющая два нейрона будет усиливатьося, если в процессе обучения оба нейрона согласованно испытывают возбуждение либо торможение. Простой алгоритм, реализующий такой механизм обучения, получил название правила Хебба. Рассмотрим его подробно.

Синхронный и асинхронный вариант активации

Рассмотрим поведение сети во времени при фиксированной матрице весов. Пускай в момент t=0 мы предали вектору состояния некоторое значение. Существуют два варианта дальнейшего процесса работы сети: синхронный и асинхронный. Синхронный вариант работы заключается в том, что все нейроны одновременно изменят своё состояние в момент t+1 согласно состоянию сети на момент t. В случае асинхронной работы в момент t+1 своё состояние изменяет только один нейрон, в момент t+2 некоторый другой нейрон согласно состоянию сети в момент t+1 и т.д. (каждый раз нейрон выбирается случайно). В любом случае с течением времени сеть каким-то образом изменяет своё состояние. Утверждается, что при наложенных нами условиях на матрицу весов сеть через какое-то конечное время придёт в стационарное состояние, то есть. Так же утверждается, что это стационарное состояние S достигается и является одним и тем же вне зависимости от синхронности работы нейронов.

Машины Больцмана (Вероятностная сеть)

Одним из основных недостатков сети Хопфилда является тенденция «стабилизации» выходного сигнала в локальном, а не в глобальном минимуме. Желательно, чтобы сеть находила глубокие минимумы чаще, чем мелкие, и чтобы относительная вероятность перехода сети в один из двух различных минимумов зависела только от соотношения их глубин. Это позволило бы управлять вероятностями получения конкретных выходных векторов путем изменения профиля энергетической поверхности системы за счет модификации весов связей.
Идея использования «теплового шума» для выхода из локальных минимумов и повышения вероятности попадания в более глубокие минимумы принад¬лежит С. Кирпатрику. На основе этой идеи разработан алгоритм имитации отжига.
Введем некоторый параметр t — аналог уровня теплового шума. Тогда вероятность активности некоторого нейрона к определяется на основе вероятност¬ной функции Больцмана:
Рk=1/(1 + ехр(-Еk/t)) (11)
где t — уровень теплового шума в сети; Ек — сумма весов связей к-го нейрона со всеми активными в данный момент нейронами. Кривая изменения вероятности активности к-го нейрона показана на рисунке 5. При уменьшении t колебания активности нейрона уменьшаются; при t = 0 кривая становится пороговой.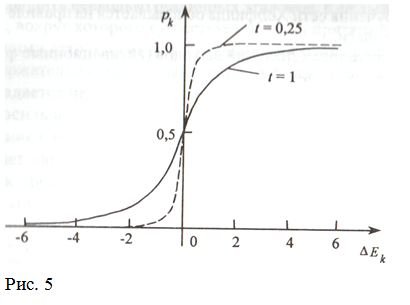

Изменение вероятности активности нейрона в зависимости от параметра t.
Специалисты по статистике называют такие сети случайными марковскими полями. Сеть, использующая для обучения алгоритм имитации отжига, назвается машиной Больцмана в честь австрийского физика Л. Больцмана, одного из создателей статистической механики. Сформулируем задачу обучения вероятностной сети, в которой вероятность активности нейрона вычисляется по формуле (11). Пусть для каждого набора возможных входных векторов требуется получить с определенной вероятностью все допустимые выходные вектора. В большенстве случаев эта вероятность близка к нулю. Процедура обучения машины Больцмана сводится к выполнению следующих чередующихся шагов:
1) Подать на вход сети входной вектор и зафиксировать выходной (как в процедуре обучения с учителем). Предоставить сети возможность приблизиться к состоянию теплового равновесия:
а) приписать состоянию каждого нейрона с вероятностью рк (см. формулу (7.2)) значение единица (активный нейрон) и с вероятностью 1-рк — нуль (не активный нейрон);
б)уменьшить параметр t, перейти к а).
В соответствии с правилом Хебба увеличить вес связи между активными нейронами на величину δ. Эти действия повторить для всех пар векторов обучающей выборки.
2) Подать на вход сети входной вектор без фиксации выходного вектора. Повторить пункты а), б). Уменьшить вес связи между активными нейронами на величину δ.
Результирующее изменение веса связи между двумя произвольно взятыми нейронами на определенном шаге обучения будет пропорционально разности между вероятностями активности этих нейронов на 1-м и 2-м шаге. При повто¬рении шагов 1 и 2 эта разность стремится к нулю.
Второй способ обучения – обучение без учителя – заключается в предварительном расчете коэффициентов в матрице весов. Данные расчеты основаны на предварительном знании условия решаемой задачи.

Друзья, это пока все что я успел вспомнить и найти в своих запасниках.
В следующей статье хочу описать уже прикладной аспект этого вопроса, а именно разработку программы использующую алгоритм Машины Больцмана. Решение будет на задача коммивояжора.
Всем спасибо за внимание.
Очень жду комментариев и вопросов.

Источник

Глубокое обучение встречает физику: ограниченные машины Больцмана, часть I

Дата публикации Apr 27, 2018

Это руководство является частью серии из двух статей о Restricted Boltzmann Machines, мощной архитектуре глубокого обучения для совместной фильтрации. В этой части я познакомлю вас с теорией ограниченных машин Больцмана. Вторая часть состоит из пошагового руководства по практической реализации модели, которая может предсказать, хочет ли пользователь фильм или нет.

Практическая часть теперь доступнаВот,

Оглавление:

0. Введение

1. Ограниченные машины Больцмана

1.1 Архитектура

На мой взгляд, RBM имеют одну из самых простых архитектур из всех нейронных сетей. Как видно на рис.1. RBM состоит из одного входного / видимого слоя (v1,…, v6), одного скрытого слоя (h1, h2) и соответствующих векторов смещения Bias и уклонб, Отсутствие выходного слоя очевидно. Но, как будет видно позже, выходной слой не понадобится, поскольку прогнозы делаются иначе, чем в обычных нейронных сетях с прямой связью.

1.2 Модель на основе энергии

Одной из целей моделей глубокого обучения является кодирование зависимостей между переменными. Захват зависимостей происходит посредством связывания скалярной энергии с каждой конфигурацией переменных, что служит мерой совместимости. Высокая энергия означает плохую совместимость. Модель на основе энергии всегда старается минимизировать предопределенную энергетическую функцию. Энергетическая функция для RBM определяется как:

Как можно заметить, значение энергетической функции зависит от конфигурации видимого / входного состояний, скрытых состояний, весов и смещений. Обучение RBM состоит в нахождении параметров для заданных входных значений, чтобы энергия достигала минимума.

1.3 Вероятностная модель

Ограниченные машины Больцмана являются вероятностными. В отличие от назначения дискретных значений модель присваивает вероятности. В каждый момент времени RBM находится в определенном состоянии. Состояние относится к значениям нейронов в видимом и скрытом слояхvа такжечас, Вероятность того, что определенное состояниеvа такжечасМожно наблюдать, дает следующее совместное распределение:

ВотZназывается «функцией разбиения», которая является суммированием по всем возможным парам видимых и скрытых векторов.

Это тот момент, когда ограниченные машины Больцмана встречаются с физикой во второй раз. Совместное распределение известно в физике какРаспределение Больцманачто дает вероятность того, что частица может наблюдаться в состоянии с энергиейЕ, Как и в физике, мы назначаем вероятность наблюдать состояниеvа такжечас,это зависит от общей энергии модели. К сожалению, очень сложно рассчитать общую вероятность из-за огромного количества возможных комбинацийvа такжечасв функции разделаZ, Гораздо проще вычисление условных вероятностей состояниячасучитывая состояниеvи условные вероятности состоянияvучитывая состояниечас:

Вотσсигмовидная функция. Это уравнение получено путем применения правила Байеса к уравнению 3 и его большого расширения, которое здесь не рассматривается.

Аналогична вероятность, что бинарное состояние видимого нейронаяустановлен в 1:

2. Совместная фильтрация с ограниченными машинами Больцмана

2. 1 Распознавание скрытых факторов в данных

Предположим, что некоторых людей попросили оценить набор фильмов по шкале от 1 до 5 звезд. В классическом факторном анализе каждый фильм можно объяснить с точки зрения набора скрытых факторов. Например, фильмы типаГарри Поттера такжеФорсажможет иметь сильные ассоциации со скрытыми факторамифантазияа такжедействие, С другой стороны, пользователи, которые любятИстория игрушека такжеWall-Eможет иметь сильные ассоциации со скрытымPixarфактор. УОКР используются для анализа и выяснения этих основных факторов. После нескольких эпох фазы обучения нейронная сеть видела все оценки в наборе дат обучения для каждого пользователя, умноженного на несколько раз. В это время модель должна была узнать скрытые факторы, основанные на предпочтениях пользователей и соответствующих совместных вкусов фильмов всех пользователей.

Учитывая фильмы, юань назначает вероятностьр (ч | v)(Уравнение 4) для каждого скрытого нейрона. Окончательные двоичные значения нейронов получены путем выборки изРаспределение Бернуллииспользуя вероятностьп,

В этом примере только скрытый нейрон, который представляет жанрФантазиястановится активным. С учетом рейтингов фильма машина Restricted Boltzmann правильно распознала, что нравится пользователюФантазиябольшинство.

2.2 Использование скрытых факторов для прогнозирования

После этапа обучения цель состоит в том, чтобы предсказать двоичный рейтинг фильмов, которые еще не были просмотрены. Учитывая данные обучения конкретного пользователя, сеть может идентифицировать скрытые факторы, основываясь на предпочтениях этого пользователя. Поскольку скрытые факторы представлены скрытыми нейронами, мы можем использоватьр (v | ч)(Уравнение 5) и выборка из распределения Бернулли, чтобы выяснить, какой из видимых нейронов теперь становится активным.

На рис. 4 показаны новые оценки после использования скрытых значений нейронов для вывода. Сеть определилаФантазиякак предпочтительный жанр фильма и рейтингХоббиткак фильм, который хотел бы пользователь.

В итоге процесс от обучения до прогнозирования проходит следующим образом:

3. Обучение

Обучение Restricted Boltzmann Machine отличается от обучения регулярных нейронных сетей посредством стохастического градиентного спуска. Отклонение процедуры обучения для RBM не будет здесь рассмотрено. Вместо этого я дам краткий обзор двух основных этапов обучения и рекомендую читателю этой статьи ознакомиться с оригинальной статьей оОграниченные машины Больцмана,

3.1 Выборка Гиббса

Первая часть тренинга называетсяВыборка Гиббса, Учитывая входной векторvмы используемр (ч | v)(Уравнение 4) для прогнозирования скрытых значенийчасЗная скрытые ценности, которые мы используемр (v | ч)(Уравнение 5) для прогнозирования новых входных значенийv, Этот процесс повторяетсяКраз ПослеКитерации мы получаем другой входной векторV_kкоторый был воссоздан из исходных значений вводаv_0,

3.2 Контрастное расхождение

Обновление весовой матрицы происходит во времяКонтрастное расхождениешаг. векторыv_0а такжеV_kиспользуются для расчета вероятностей активации для скрытых значенийh_0а такжеh_k(Eq.4). Разница междувнешние продуктыиз этих вероятностей с входными векторамиv_0а такжеV_kРезультаты в матрице обновления:

Используя матрицу обновления, новые веса могут быть рассчитаны с градиентомподъем,дано:

Специальное объявление: Мы только что выпустили бесплатный курс по глубокому обучению!

Я основательАкадемия глубокого обучения, продвинутая образовательная платформа Deep Learning. Мы предоставляем практическое современное глубокое обучение, обучение и наставничество для профессионалов и начинающих.

Среди наших вещей мы только что выпустилибесплатный вводный курс по глубокому обучению с TensorFlow, где вы можете узнать, как реализовать нейронные сети с нуля для различных сценариев использования с использованием TensorFlow.

Если вы заинтересованы в этой теме, не стесняйтесь проверить это;)

Источник

Ограниченная машина Больцмана

Введение в ограниченную машину Больцмана

Работа машины Restricted Boltzmann

Каждый видимый узел получает низкоуровневое значение от узла в наборе данных. В первом узле невидимого слоя Х образуется произведением веса и добавляется к смещению. Результат этого процесса подается на активацию, которая вырабатывает мощность данного входного сигнала или выхода узла.

В следующем процессе несколько входов будут соединены в одном скрытом узле. Каждый X объединяется по индивидуальному весу, добавление продукта объединяется со значениями, и снова результат передается через активацию, чтобы дать вывод узла. В каждом невидимом узле каждый вход X объединяется с индивидуальным весом W. Здесь вход X имеет три веса, что составляет двенадцать вместе. Вес, сформированный между слоями, становится массивом, где строки являются точными для входных узлов, а столбцы удовлетворяются для выходных узлов.

Каждый невидимый узел получает четыре ответа, умноженные на их вес. Добавление этого эффекта снова добавляется к значению. Это действует как катализатор для некоторого процесса активации, и результат снова подается в алгоритм активации, который производит каждый отдельный вывод для каждого невидимого ввода.

Первая модель, полученная здесь, это модель на основе энергии. Эта модель связывает скалярную энергию с каждой конфигурацией переменной. Эта модель определяет распределение вероятностей через энергетическую функцию следующим образом:

(1)

В этой энергетической функции следует логистическая регрессия, которая на первом этапе будет определять лог. вероятность и следующий определит функцию потерь как отрицательную вероятность.

используя стохастический градиент, где параметры,

Энергетическая модель со скрытой единицей определяется как ‘h’

Наблюдаемая часть обозначается как «х»

Из уравнения (1) уравнение свободной энергии F (x) определяется следующим образом

(2)

(3)

Отрицательный градиент имеет следующую форму,

(4)

Вышеупомянутое уравнение имеет две формы, положительную и отрицательную форму. Термин положительный и отрицательный не представлен знаками уравнений. Они показывают влияние плотности вероятности. Первая часть показывает вероятность уменьшения соответствующей свободной энергии. Вторая часть показывает снижение вероятности генерируемых образцов. Затем градиент определяется следующим образом:

(5)

Здесь N отрицательные частицы. В этой основанной на энергии модели трудно определить градиент аналитически, так как он включает в себя расчет

Следовательно, в этой модели EBM мы имеем линейное наблюдение, которое не может точно отобразить данные. Таким образом, в следующей модели Restricted Boltzmann Machine скрытый слой предназначен для обеспечения высокой точности и предотвращения потери данных. Энергетическая функция RBM определяется как,

(6)

В RBM единицы видимого и скрытого слоя полностью независимы, что можно записать следующим образом:

Из уравнений 6 и 2, вероятностный вариант функции активации нейрона,

(7)

(8)

Это далее упрощается в

(9)

Объединяя уравнения 5 и 9,

(10)

Отбор проб в Restricted Boltzmann machine

Выборка Гиббса сустава из N случайных величин выполняется через последовательность из N подэтапов выборки вида где

содержит другие случайные величины в без учета.

Вот, это набор всех скрытых юнитов. Пример случайным образом выбирается равным 1 (против 0) с вероятностью, и так же, случайным образом выбирается равным 1 (против 0) с вероятностью

Контрастное расхождение

Он используется в качестве катализатора для ускорения процесса отбора проб
Поскольку мы ожидаем, чтобы быть правдой, мы ожидаем значение распределения должно быть близко к P, так что оно образует сходимость к окончательному распределению P

Но противоречивая дивергенция не ждет, когда цепь сойдется. Образец получается только после процесса Гиббса, поэтому мы установили здесь k = 1, где он работает на удивление хорошо.

Стойкая контрастная дивергенция

Это еще один метод аппроксимации формы выборки. Это постоянное состояние для каждого метода выборки, он извлекает новые выборки, просто изменяя параметры K.

Слои машины Restricted Boltzmann

Примеры

Преимущества машины Restricted Boltzmann

Вывод

Рекомендуемая статья

Это было руководство к ограниченной машине Больцмана. Здесь мы обсуждаем его работу, отбор проб, преимущества и машину Layers of Restricted Boltzmann. Вы также можете просмотреть наши другие предлагаемые статьи, чтобы узнать больше _

Источник