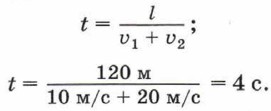Опишите движение двух автомобилей представленное графиками зависимости

Равномерное прямолинейное движение

4. Зависимость координаты тела от времени можно представить графически.

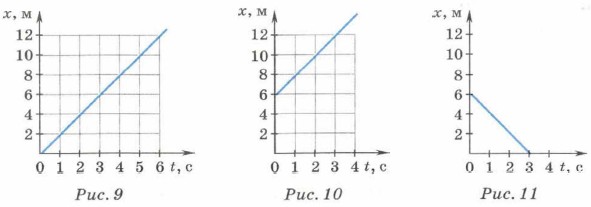
Предположим, что тело движется из начала координат в направлении оси X с постоянной скоростью. Проекция скорости тела на эту ось равна 2 м/с. Уравнение движения в этом случае имеет вид: х = 2t (м). Зависимость координаты тела от времени — линейная. Графиком такой зависимости является прямая, проходящая через начало координат (рис. 9).

Если в начальный момент времени координата тела х₀ = 6 м, а проекция его скорости υ_x = 2 м/с, то уравнение движения имеет вид: х = 6 + 2t (м). Это тоже линейная зависимость координаты тела от времени, и её графиком является прямая, проходящая через точку, для которой при t = 0 x = 6m (рис. 10).

Таким образом, движение тела может быть описано аналитически, т. е. с помощью уравнения движения, и графически, т. е. с помощью графика зависимости координаты тела от времени.

5. Пример решения задачи

При решении задач необходимо выполнять следующую последовательность действий.

1. Кратко записать условие задачи.

2. Проанализировать ситуацию, описанную в условии задачи:

— выяснить, можно ли принять движущиеся тела за материальные точки;

— сделать рисунок, изобразив на нём векторы скорости;

— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.

3. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости на координатные оси.

4. Решить задачу в общем виде.

5. Подставить в формулу значения величин и выполнить вычисления.

6. Проанализировать ответ.

Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один — со скоростью 10 м/с, другой — со скоростью 20 м/с. Определите время и координату места встречи автомобилей, если в начальный момент времени расстояние между ними равно 120 м.

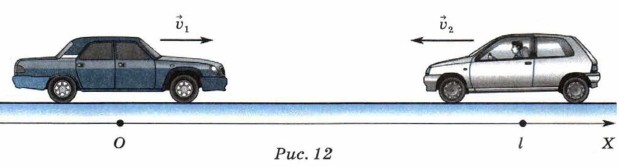
1-й способ. Свяжем систему отсчёта с Землёй, ось ОХ направим в сторону движения первого автомобиля, за начало отсчёта координаты выберем точку О — положение первого автомобиля в начальный момент времени (рис. 12).

В начальный момент времени координаты каждого тела равны: х₀₁ = 0; х₀₂ = l.

Запишем уравнение движения: х = х₀ + vυ_xt.

Уравнения движения для каждого тела с учётом начальных условий имеют вид:

В момент встречи тел х₁ = х₂, следовательно:

Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей:

х = 10 м/с • 4 с = 40 м.

Источник

Опишите движение двух автомобилей представленное графиками зависимости

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Типовая задача «Уравнение координаты (нахождение неизвестной величины)»

Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»

Задача № 2. Движение двух тел задано уравнениями x₁ = 20 – 8t и х₂ = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»

Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.

Типовая задача «График координаты. Движение нескольких тел»

Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.

ЗАДАЧИ ПОСЛОЖНЕЕ

Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ:

РЕШЕНИЕ:

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.

Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.

Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.

При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.

В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:

Источник

Опишите движение двух автомобилей представленное графиками зависимости

На рисунке представлен график зависимости пути S велосипедиста от времени t.

Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью

Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась

На других интервалах скорость была иная.

Правильный ответ указан под номером 4.

а на интервале от 10 до 30, он же тоже двигается 5 м/с

На этом интервале пройденный им путь не изменяется, а значит, он покоится.

Тоесть,он двигается со скоростью 5м/c,но пройденный путь не изменяется?

Нет, раз его путь не изменяется, значит его скорость на этом интервале времени равна нулю.

А в интервале времени от 50 до 70 сек,разве скорость равнялась не 5м/c? 100м/20c=5(м/c)

В интервале от 50 до 70 с скорость велосипедиста равнялась

На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.

Пункт A находится в точке а пункт Б — в точке Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)

Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна

Здесь использована формула для движения без ускорения. Но если всмотреться в график, то можно заметить, что за первые 0,1ч автобус прошел 5км. За вторые 0,1 км автобус проехал уже больше 5км.

То есть движение-то получается не равномерное.

Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)

Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки: Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение:

что в этой задаче является

1. скоростью относительно неподвижной с.о.

2. скоростью относительно подвижной с.о.

3. переносной скоростью

1. скорость относительно неподвижной с.о. — скорость пловца относительно берега ;

2. скорость относительно подвижной с.о. — скорость пловца относительно воды ;

3. переносная скорость — скорость воды относительно берега .

Если бы он бы плыл против течения, то ответ был бы 0,1 м/с?

Все верно, но была бы она направлена в противоположную сторону.

Ваше решение совершенно верно. Однако есть некоторая небрежность в определении переносной скорости.

Переносной скоростью нельзя называть скорость движения системы отсчета, тем более при вращательном движении СО понятие скорости СО вообще исчезает, так как разные ее точки имеют разные скорости.

Итак, Vа=Vп+Vо (в формулах все величины векторные). С определением абсолютной и относительной скорости нет проблем. Так что же такое переносная скорость? Определение легко дать, исходя из самой формулы. Если Vо=0, то Vа=Vп. То есть переносная скорость это скорость точки в неподвижной системе, если в подвижной системе она покоится. Это скорость, с которой подвижная система переносит относительно неподвижной покоящуюся на ней точку. Потому она и называется переносной.

Из такого понятия и вытекает, что в нашем случая скорость течения реки и есть переносная скорость.

Спасибо за уточняющий комментарий.

Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)

Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: То есть, буквально, надо весь пройденный телом путь разделить на всё время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.

Разберёмся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.

Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через L, тогда весь путь, пройденный велосипедистом, равен На первую половину пути велосипедист затратил время На обратную дорогу — время Всё время пути составило Окончательно, находим, что средняя путевая скорость велосипедиста равна

Источник

Опишите движение двух автомобилей представленное графиками зависимости

На рисунке приведён график зависимости модуля средней скорости V_р материальной точки от времени t при прямолинейном движении. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

3) За первые 3 с движения материальная точка проходит путь 8 м.

4) За первые 2 с движения материальная точка проходит путь 12 м.

5) Модуль начальной скорости материальной точки равен 2 м/с.

При равноускоренном движении средняя скорость равна полусумме начальной и конечной скорости. Найдем, чему равна скорость тела в момент времени t = 1 c:

Таким образом, ускорение тела равно

Путь — это произведение средней скорости на затраченное время

Обратите внимание, что на графике приведена зависимость средней скорости от времени, а не просто скорости. Наклон этого графика не равен ускорению.

Грузик массой m = 100 г неподвижно висит на лёгкой абсолютно упругой гибкой резинке с коэффициентом упругости k = 100 Н/м в поле силы тяжести с ускорением свободного падения g. Грузик поднимают из этого положения вертикально вверх на высоту h = 80 см, меньшую длины резинки, и отпускают без начальной скорости. Найдите время движения грузика вниз до точки его остановки. Начальной деформацией резинки при покоящемся грузике можно пренебречь.

Какие законы Вы используете для описания движения груза на резинке? Обоснуйте их применение к данному случаю.

Обоснование. Грузик движется поступательно, поэтому его можно принять за материальную точку. На первом этапе движения грузика на него действует только сила тяжести, т. к. сопротивлением воздуха мы пренебрегаем. Следовательно, на этом этапе грузик движется с ускорением свободного падения. И для описания движения тела можно применять законы прямолинейного равноускоренного движения.

На втором этапе движения резинка упруго деформируется, в результате чего на грузик начинает действовать изменяющаяся по модулю и направлению сила упругости, для которой справедлив закон Гука. Таким образом, второй этап движения представляет собой механические колебания груза на резинке. Т. к. сила тяжести не меняется по модулю и направлению, то она не влияет на характер колебаний грузика. В инерциальной системе отсчета возможно применение законов колебательного движения.

Перейдем к решению.

1. Введём неподвижную декартову систему координат с вертикальной осью ОХ, направленной вниз, причём начало координат поместим на уровне начального положения грузика.

2. После подъёма и отпускания грузика его движение вниз в поле силы тяжести разбивается на две стадии: вначале он свободно падает с ускорением g с высоты h до точки x = 0 (поскольку начальной деформацией резинки можно пренебречь) за время

что следует из формул кинематики равноускоренного движения.

3. Затем резинка начинает растягиваться, а грузик — тормозиться вплоть до остановки в нижней точке его движения. Поскольку начальное растяжение резинки компенсирует вес грузика, то на второй стадии можно считать, что действует только упругая сила, и уравнение движения (второй закон Ньютона) в проекции на ось ОХ имеет вид:

что является уравнением гармонических колебаний с периодом

4. С учётом начальных условий закон движения грузика на втором этапе представляет собой 1/4 часть периода синусоиды и происходит за время

5. Таким образом, искомое время движения грузика вниз до точки остановки равно

6. Подставляя численные данные из условия, получаем:

Ответ:

Источник

Опишите движение двух автомобилей представленное графиками зависимости

По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале времени от 0 до 2 с автомобиль прошёл путь

Примечание. В принципе, интересующий нас участок (от 0 до 2 с) не обязательно разбивать на два, площадь под графиком можно посчитать, как площадь трапеции:

В принципе, можно использовать стандартные кинематические формулы для изменения координаты, скорости, ускорения, а все необходимые данные снимать с графика. Но так получается значительно дольше.

Почему же не через площадь дольше?

S= So + vt + (at^2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;

Правильно. Так тоже можно.

В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.

В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂

Утверждение «в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)» не совсем верно, правильно тогда уж говорить так: «за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с».

Однако такое утверждение в свою очередь требует разъяснений.

так путь же нужно найти почему нельзя воспользоваться формулой S=Vt

Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется

В задании не сказано, но тело двигалось прямолинейно

Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.

На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Источник