Определить является ли p словом ab машина тьюринга
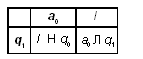
Машина Тьюринга. Определить, входит ли в слово P символ a
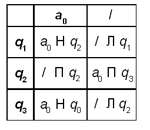
Машина Тьюринга: оставить в слове P только последний символ (пустое слово не менять)
Помогите решить A=
Машина Тьюринга: оставить в слове Р только последний символ (пустое слово не менять)
A=
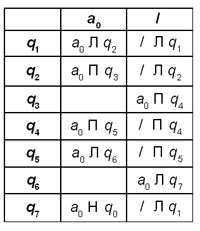
Машина Тьюринга: если P-непустое слово, то за его первым символом вставить символ а
Если P-непустое слово, то за его первым символом вставить символ а. Алфавит А:
Машина Тьюринга: Если первый и последний символ непустого слова различаются, то заменить слово пустым
Здравствуйте,помогите решить задачу. Если первый и последний символ непустого слова различаются.
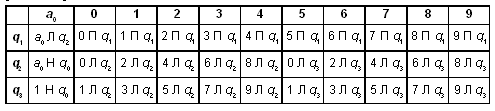
Определить, какое слово перерабатывает машина Тьюринга из данных слов.
Вот собственно два задания Помогите решить, одно начал, но не знаю как дальше 1 задание: 2.
Машина Тьюринга: после знака «=» вывести символ алфавита, входящий в слово в минимальном количестве
Слово в алфавите abc. После знака = вывести символ алфавита, входящий в слово в минимальном.
Машина Тьюринга. В итоговом ответе записать что получившиеся слово = a0 a0 a0 a0 a0 или слово = 0
Я решил задачу: После применения машины Тьюринга к слову a=11*11, у меня вышло после применения.
Машина Тьюринга
Содержание
Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.
Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:
При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.
Определение [ править ]
Определение машины [ править ]
Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.
Определение процесса работы [ править ]
Особо следует рассмотреть случай переходов по пробельному символу:
Для машины Тьюринга, которая пишет символ [math]B[/math] на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.
Результат работы [ править ]
Примеры машин-распознавателей и машин-преобразователей будут даны ниже.
Примеры машин Тьюринга [ править ]
Прибавление единицы [ править ]
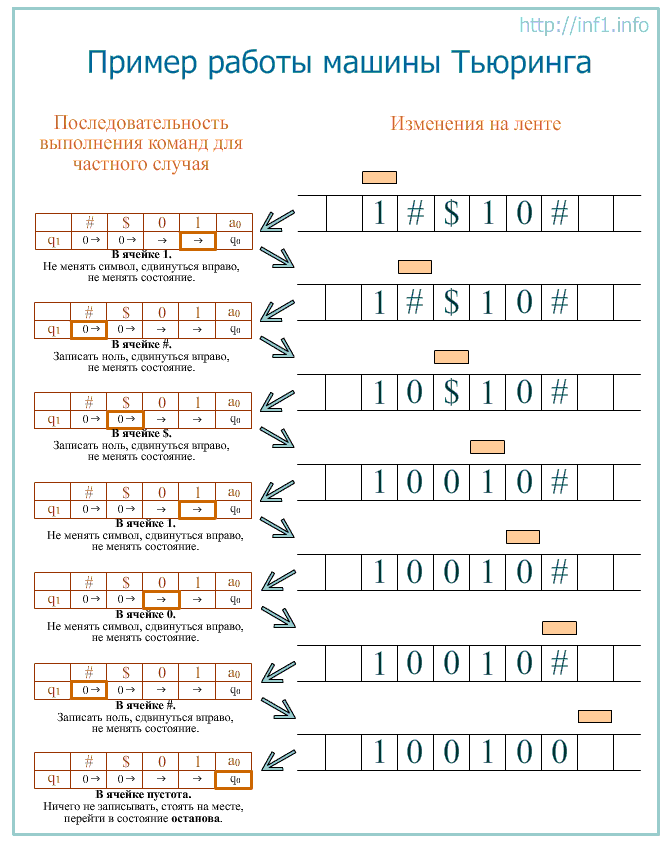
Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:
| [math]0[/math] | [math]1[/math] | [math]B[/math] | |
| [math]S[/math] | [math]\langle R, 1, \downarrow \rangle[/math] | [math]\langle S, 0, \rightarrow \rangle[/math] | [math]\langle R, B, \leftarrow \rangle[/math] |
| [math]R[/math] | [math]\langle R, 0, \leftarrow \rangle[/math] | [math]\langle R, 1, \leftarrow \rangle[/math] | [math]\langle Y, B, \rightarrow \rangle[/math] |
Проверка того, является ли слово палиндромом [ править ]
| [math]0[/math] | [math]1[/math] | [math]B[/math] | |
| [math]S[/math] | [math]\langle F_0, B, \rightarrow \rangle[/math] | [math]\langle F_1, B, \rightarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]F_0[/math] | [math]\langle F_0, 0, \rightarrow \rangle[/math] | [math]\langle F_0, 1, \rightarrow \rangle[/math] | [math]\langle B_0, B, \leftarrow \rangle[/math] |
| [math]F_1[/math] | [math]\langle F_1, 0, \rightarrow \rangle[/math] | [math]\langle F_1, 1, \rightarrow \rangle[/math] | [math]\langle B_1, B, \leftarrow \rangle[/math] |
| [math]B_0[/math] | [math]\langle R, B, \leftarrow \rangle[/math] | [math]\langle N, 1, \downarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]B_1[/math] | [math]\langle N, 0, \downarrow \rangle[/math] | [math]\langle R, B, \leftarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]R[/math] | [math]\langle R, 0, \leftarrow \rangle[/math] | [math]\langle R, 1, \leftarrow \rangle[/math] | [math]\langle S, B, \rightarrow \rangle[/math] |
Варианты машины Тьюринга [ править ]
В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.
Многодорожечная машина Тьюринга [ править ]
Машина Тьюринга с полубесконечной лентой [ править ]
Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.
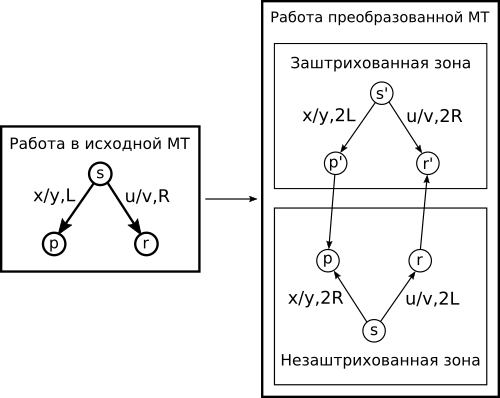
Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом:
Затем перенумеруем ячейки, и запишем символ [math]c \in \Pi \setminus \Sigma, B[/math] в начало ленты, который будет означать границу рабочей зоны:
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации.
Многоленточная машина Тьюринга [ править ]
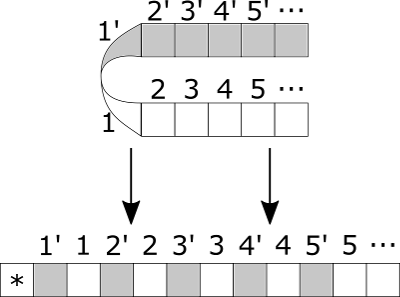
Многоленточная машина с [math]n[/math] дорожками эмулируется многодорожечной машиной с [math]2n[/math] дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом [math]*[/math] позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).
Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов [math]*[/math] символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.
Аланом Тьюрингом было сформулировано следующее утверждение:



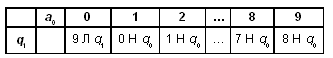
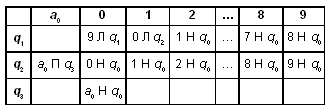
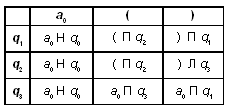
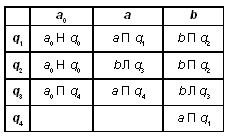


 Проверить, одинаковы ли первые две буквы слова (regex)
Проверить, одинаковы ли первые две буквы слова (regex)