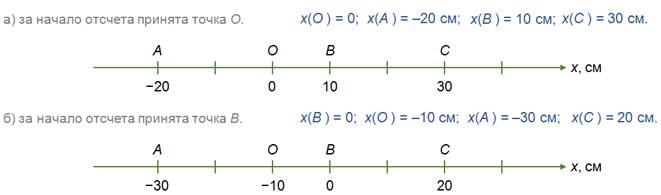При движении автомобиля траектория точки обода колеса
Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
При движении автомобиля траектория точки обода колеса
Рис. 3.2. Циклоида как траектория точки обода катящегося колеса
Циклоиду можно рассматривать как траекторию какой-либо точки обода колеса, которое катится без проскальзывания по прямой. На рис. 3.2 показана циклоида, которую «вычерчивает» точка 𝐴, находившаяся внизу в начальный момент. Точка 𝐴 описывает данную циклоиду независимо от того, катится ли колесо равномерно или с ускорением, важно только, чтобы оно не проскальзывало. Проще всего рассмотреть, разумеется, равномерное качение колеса. Такое качение получается в результате сложения равномерного вращения колеса вокруг оси и равномерного поступательного движения, линейная скорость которого 𝑣 равна произведению угловой скорости на радиус колеса 𝑟.
Во всех инерциальных системах отсчёта материальная точка имеет одно и то же ускорение. Поэтому находить его можно в любой такой системе отсчёта. Ясно, что ускорение точек обода колеса связано только с его вращением вокруг оси. Поэтому ускорение 𝑎 любой точки обода направлено по радиусу к центру колеса и определяется выражением
Значит, и в высшей точке циклоиды ускорение элемента обода колеса равно 𝑣²/𝑟 и направлено вниз (рис. 3.2).
Теперь рассмотрим движение этой же точки обода как движение по циклоиде. Скорость в любой точке траектории направлена по касательной к ней; значит, в высшей точке циклоиды скорость направлена горизонтально. Ускорение же, как мы выяснили, направлено вертикально вниз, т.е. перпендикулярно скорости. Поэтому найденное выше ускорение может быть записано также в виде
Для нахождения 𝑉 будем рассуждать следующим образом. Скорость любой точки обода катящегося колеса равна векторной сумме скорости поступательного движения колеса и линейной скорости вращения вокруг оси. При отсутствии проскальзывания эти скорости равны по модулю. В верхней точке они и направлены одинаково. Поэтому 𝑉=2𝑣, и, сравнивая формулы (1) и (2), находим
Радиус кривизны циклоиды в верхней точке равен удвоенному диаметру колеса. Если бы мы рассматривали качение колеса как вращение вокруг мгновенной оси, совпадающей в каждый момент с нижней неподвижной точкой колеса (рис. 3.2), то могло бы показаться, что верхняя точка движется по окружности, радиус которой равен диаметру колеса. Так оно и было бы, если бы мгновенная ось вращения 𝑂 оставалась неподвижной. На самом деле эта ось перемещается вместе с колесом, и именно поэтому рассматриваемая точка обода 𝐴 движется в этот момент по окружности, радиус которой даётся формулой (3). ▲
4. Падающий мяч.
Заброшенный в кольцо баскетбольный мяч начинает отвесно падать из корзины без начальной скорости. В тот же момент из точки, находящейся на расстоянии 𝑙 от кольца, в падающий мяч бросают теннисный мяч (рис. 4.1). С какой начальной скоростью был брошен теннисный мяч, если мячи столкнулись на расстоянии ℎ от кольца?
Рис. 4.1. Падающий мяч
△ В поставленном вопросе подразумевается, что нужно найти вектор начальной скорости теннисного мяча, т.е. его направление (угол α) и модуль (𝑣₀). Если решать задачу в исходной (лабораторной) системе отсчёта, то ход рассуждений может быть следующим. Записываем выражения для перемещений обоих мячей за время 𝑡 от начала движения до их встречи, затем проецируем их на вертикальное и горизонтальное направления (рис. 4.2). В результате приходим к системе уравнений
Рис. 4.2. Проекции перемещений мячей
В системе трёх уравнений (1) четыре неизвестных величины: 𝑣₀, α, 𝑡 и 𝐻. Поэтому может показаться, что задача не имеет единственного решения. Однако это не так. Действительно, подставляя ℎ из первого уравнения во второе, получаем
Разделив почленно это уравнение на третье уравнение системы (1), находим выражение для tg α:
Теперь с помощью рис. 4.2 можно увидеть, что угол α, под которым должна быть направлена начальная скорость теннисного мяча, в действительности соответствует направлению из точки бросания на кольцо. Истинное направление начальной скорости 𝒗₀ показано на рис. 4.3. Итак, бросать теннисный мяч нужно точно в направлении кольца. Модуль его начальной скорости можно найти, подставляя 𝑡=√2ℎ/𝑔 из первого уравнения системы (1) в уравнение (2). Учитывая, что 𝐻/sin α=𝑙, получаем
Рис. 4.3. Истинное направление вектора 𝑣₀ начальной скорости
Но всех этих преобразований можно избежать, если с самого начала перейти в систему отсчёта, связанную с баскетбольным мячом, т.е. свободно падающую с ускорением 𝒈 в этой системе отсчёта баскетбольный мяч, естественно, неподвижен, а теннисный движется равномерно и прямолинейно со скоростью 𝒗₀. Очевидно, что эта скорость 𝒗₀ должна быть направлена на баскетбольный мяч. Через время 𝑡=𝑙/𝑣₀ мячи столкнутся. В лабораторной системе отсчёта за это время баскетбольный мяч опустится на расстояние
откуда для 𝑣₀ получаем прежнее выражение (4). На примере этой задачи мы видим, что в некоторых случаях удобным оказывается переход в ускоренно движущуюся систему отсчёта. ▲
5. В цель с наименьшей начальной скоростью.
Необходимо с поверхности земли попасть камнем в цель, которая расположена на высоте ℎ и на расстоянии 𝑠 по горизонтали. При какой наименьшей начальной скорости камня это возможно? Сопротивлением воздуха пренебречь.
△ На первый взгляд кажется, что начальная скорость камня будет наименьшей, если верхняя точка его траектории совпадает с мишенью (рис. 5.1а).
Рис. 5.1. К выбору оптимальной траектории
Может быть, и вам так показалось? Иллюзия эта настолько сильна, что подобное решение аналогичной задачи можно встретить в некоторых солидных пособиях по решению физических задач. Однако, даже не решая задачи, легко убедиться, что это не так. Действительно, будем мысленно уменьшать высоту, на которой расположена цель. При этом точка, куда попадает камень, продолжает согласно предположению оставаться верхней точкой траектории (рис. 5.1б), в том числе и в предельном случае ℎ=0. Но совершенно очевидно, что для того чтобы попасть в цель, находящуюся на земле, достаточно просто добросить камень до цели (рис. 5.1б). Итак, предположение о том, что цель совпадает с высшей точкой траектории полёта камня, неверно.
Какую траекторию описывают при движении автомобиля его фара, точка обида колеса, центр колеса : а) относительно прямолинейного шоссе ; б) относительно центра колеса?
Какую траекторию описывают при движении автомобиля его фара, точка обида колеса, центр колеса : а) относительно прямолинейного шоссе ; б) относительно центра колеса.
Помогите пожалуйста СРОЧНО.
Κυκλοειδής— круглый)—плоская трансцендентная кривая.
Циклоида определяется кинематически кактраекторияфиксированной точкипроизводящейокружности радиуса, катящейся без скольжения попрямой.
Мне кажется : Прямую линию, параллельную дороге.
Помогите пожалуйста срочно решить задачу?
Помогите пожалуйста срочно решить задачу.
Велосипедист движется по прямолинейному гладкому участку дороги.
Каковы траектории движения относительно велосипедиста и относительно стоящего на обочине человека рамы велосипеда ; точки на ободе колеса ; руля ; точки на конце педали?
Велосипедист движется прямолинейно и равномерно?
Велосипедист движется прямолинейно и равномерно.
1)какова траектория движения центра колеса относительно дороге.
2) Что описывает ниппель относительно центра колеса.
3) Ниппель относительно рамы.
4)Точка ниппеля колеса относительно дороги Помогите пожалуйста, срочно.
Нужно описать траектории.
Колесо катится по горизонтальной дороге?
Колесо катится по горизонтальной дороге.
Центр масс колеса перемещается со скоростью vo относительно земли.
Выберите рисунок, на котором для точки C, находящейся на ободе колеса, правильно показаны вектор её центростремительного ускорения и вектор её скорости относительно земли :
Нарисуйте примерный вид траектории движения точки обода колеса относительно центра колеса?
Нарисуйте примерный вид траектории движения точки обода колеса относительно центра колеса.
Автомобиль едет равномерно со скоростью 70км / ч?
Автомобиль едет равномерно со скоростью 70км / ч.
Определите скорость камешка в тот момент, когда он находился в верхней точке своей траектории.
А) Относительно центра колеса.
В)Относительно камешка, оставшегося на дороге.
Какую траекторию при движении автомобиля описывает центр колеса автомобиля?
Какую траекторию при движении автомобиля описывает центр колеса автомобиля.
Какова траектория движения точки обода колеса мотоцикла движется прямо линейно относительно a)поверхности земли б)корпуса мотоцикла в)оси вращающегося колеса?
Какова траектория движения точки обода колеса мотоцикла движется прямо линейно относительно a)поверхности земли б)корпуса мотоцикла в)оси вращающегося колеса.
Велосепидист движется по горизонтальной прямой дороге?
Велосепидист движется по горизонтальной прямой дороге.
Нарисуйте траекторию движения точки А, отмеченной на колесе велосипеда во время движения, относительно :
1) жука, сидящего на оси колеса ;
2) муравья, сидящего в точке В на колесе ;
3) человека, стоящего на обочине дороги.
Траектория точки на ободе колеса велосипеда во время его движения является кругом относительно : А?
Траектория точки на ободе колеса велосипеда во время его движения является кругом относительно : А.
Ноги велосипедиста Г.
Пешехода, что движется навстречу велосипеду.
G = 10 F = mg = 2×10 = 20Н.
По формуле F = mg, при g = 9, 8, находим F = 2 * 9, 8 = 19, 6.
Увеличится в 2, 25 раза.
F = gm⇒m = F / g m = 100H / 10H / кг = 10кг.
, то есть площадь поперечного сечения медного стержня в 1, 141 раза больше, чем площадь поперечного сечения железного стержня.
Если вы возьмёте изолированную систему, то есть без взаимодействия с окружающей средой, то ответнет, не будет. Согласно уравнению теплового баланса, суммарное выделевшееся количество теплоты равно поглощённому количеству теплоты. Здесь я могу Вам т..
Газ : 1. Расстояние между молекулами очень большон 2. Притяжение между молекулами очень маленькое 3. Не сохраняет форму и объем Жидкость : 1. Молекулы находятся на небольшом расстоянии 2. Небольшое притяжение между молекулами 3. Сохраняет объем..
Основные понятия кинематики. Относительность движения (практика)
Урок 2. Подготовка к ЕГЭ по физике. Часть 1. Механика.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Основные понятия кинематики. Относительность движения (практика)»
В данной теме будет рассмотрено решение некоторых типовых задач по кинематике.
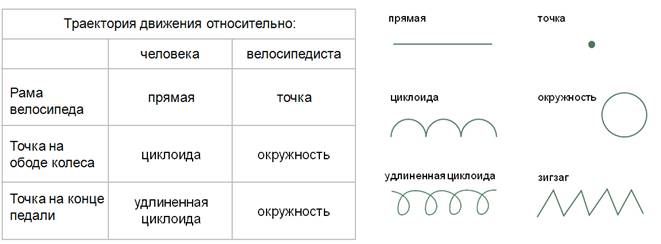
Задача 1. Велосипедист движется по прямолинейному гладкому участку дороги. Каковы траектории движения относительно велосипедиста и относительно стоящего на обочине человека рамы велосипеда; точки на ободе колеса; точки на конце педали?
Начнем с определения вида траектории рамы велосипеда. Здесь все очень просто: так как относительно велосипедиста рама неподвижна, то траекторией ее движения будет являться точка.
Относительно же человека, стоящего на обочине дороги, рама будет двигаться прямолинейно, «вычерчивая» в воздухе прямую линию.
Теперь исследуем движение точки, располагающейся на ободе колеса, относительно велосипедиста. Представьте, что вы сели на велосипед, приметили положение ниппеля на переднем колесе и не спеша надавили на педаль, не выпуская ниппель из поля зрения. Какую траекторию описывает ниппель.
Точка, располагающаяся на ободе колеса, относительно велосипедиста, описывает окружность. Аналогично будет себя вести и точка, находящаяся на конце педали
Теперь разберемся с траекторией движения точки на ободе колеса, относительно человека, стоящего на обочине. Вновь обратимся к мысленному эксперименту. Мы стоим на обочине, а мимо нас проезжает велосипедист. Зафиксировали взгляд на какой-либо точке колеса (пусть это будет, например, светоотражатель на конце спицы) и проследим за ее траекторией.
Получаются кривые, которые принадлежат семейству циклоид. Значит траекторией движения точки на ободе колеса относительно неподвижного человека на обочине является циклоида.
Траекторией движения точки на конце педали относительно неподвижного человека на обочине будет являться удлиненная циклоида.
Задача 2. Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца за месяц; в) длины экватора и г) скорости движения Земли по орбите вокруг Солнца?
Тело можно принять за материальную точку, если:
1) тело движется поступательно;
2) размеры тела много меньше расстояния, которое оно проходит;
3) размеры тела много меньше расстояния до тела отсчета.
Рассмотрим вариант а более подробно. Для это проверим выполнение выше названных условий. Согласно первому условию, тело должно двигаться поступательно. Для этого случая оно не выполняется, так как о движении Земли в условии задачи ничего не говорится. Второе условие материальной точки также не выполняется, так как не известно расстояние, пройденное Землей. По третьему условию размеры тела должны быть намного меньше расстояния до тела отсчета. В данном случае, тело отсчета — это Солнце. Среднее расстояние от Земли до Солнца составляет 149,6 миллионов км, а средний радиус нашей планеты всего 6371 км, что, конечно же, намного меньше среднего расстояния до Солнца.
Следовательно, в первом примере Землю можно принять за материальную точку, так как выполняется третье условие.
Во втором примере Землю можно принять за МТ, т. к. ее размеры много меньше расстояния, которое она проходит по орбите за месяц.
В примере «в» Землю нельзя считать МТ, т. к. при расчете длины экватора Земли нельзя пренебречь ее размерами.
В последнем примере Землю можно считать МТ, т. к. размеры Земли (радиус 6371 км) во много раз меньше расстояния до Солнца (149,6 млн. км).
Задача 3. На рисунке указаны положения точек А, О, В, С и направление оси Х. Перерисуйте рисунок и определите координаты точек, если: а) за начало отсчета принята точка О; б) за начало отсчета принята точка В.
Задача 4. Мяч вертикально упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Сделайте чертеж. Найдите путь и модуль перемещения мяча.
«Упражнение, друзья, даёт больше,