Проблема самоприменимости машины тьюринга
Проблема самоприменимости.
¨ Допустим, что существует машина T0, решающая проблему самоприменимости. Построим машину T1, в которой вместо состояния q0 введем новое заключительное состояние q0¢ и добавим к программе машины T0 новые команды
q0 0 ® 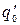
В силу тезиса Тьюринга невозможность построения машины Тьюринга означает отсутствие алгоритма решения данной проблемы. Поэтому данная теорема дает первый пример алгоритмически неразрешимой проблемы.
Проблема останова алгоритмически неразрешима. Если бы она была алгоритмически разрешимой, то взяв в качестве a код машины Т, можно было бы решить проблему самоприменимости. Данные теоремы лежат в основе доказательства алгоритмической неразрешимости большого числа алгоритмических проблем. При истолковании утверждений, связанных с алгоритмической неразрешимостью, следует иметь в виду следующее обстоятельство. Речь идет об отсутствии единого алгоритма, решающего данную проблему, при этом не исключается возможность ее решения в частных случаях.
Неразрешимость проблемы останова можно интерпретировать как несуществование общего алгоритма для отладки программ, точнее, алгоритма, который по тексту любой программы и данным для нее определял бы, зациклится ли программа на этих данных или нет.
Приведем без доказательства важную теорему теории алгоритмов.
Теорема 1.2(теорема Райса). Никакое нетривиальное свойство вычислимых по Тьюрингу функций не является алгоритмически разрешимым.
Из данной теоремы следует, что по номеру вычислимой функции нельзя узнать, является ли она постоянной, периодической, ограниченной и т.п. Смысл данной теоремы в том, что по описанию алгоритма нельзя узнать о свойствах функций, которую он вычисляет. Подчеркнем, что “нельзя узнать” означает “не существует единого алгоритма решения”. Свойства подклассов вычислимых функций могут оказаться разрешимыми.
Дата добавления: 2014-12-02 ; просмотров: 3205 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Проблема самоприменимости
Множество всех алгоритмов счетно. Это означает наличие взаимно-однозначного соответствия между алгоритмами и числами натурального ряда, т.е. функции типа
Такая функция называется нумерацией алгоритмов, а ее значение (А) – номером алгоритма А при нумерации . Из взаимной однозначности отображения следует, что существует обратная функция -1(n)= Аn, восстанавливающая по номеру n описание алгоритма Аn.
Очевидно, что различных нумераций много. Существование нумераций позволяет работать с алгоритмами как с числами. Это удобно при исследовании алгоритмов над алгоритмами. Такие алгоритмы уже рассматривались при построении универсальной машины Тьюринга и в связи с проблемой остановки. По существу, вычислимая умерация служит языком программирования для универсального алгоритма.
Теорема 1. Не существует алгоритма В(x,y) такого, что для любого алгоритма Аx (с номером (А)=х)

Один частный случай проблемы остановки имеет вполне самостоятельную интерпретацию: рассмотрим машину Т, которая решает проблему остановки для машины Т в случае, когда на ленте машины Т написана ее собственная система команд. Такая проблема называется проблемой самоприменимости машин Тьюринга. Было показано, что такая машина невозможна. В инвариантном виде это формулируется следующей теоремой
Теорема 2. Проблема самоприменимости алгоритмов аналитически неразрешима.
Т.е. не существует алгоритма В1(х) такого, что для любого Ах
Эти две теоремы являются мощным средством для доказательства разных неразрешимостей.
Решение задачи перечисления всех алгоритмов (в частности, всех рекурсивных функций) в принципе ясно. Может показаться, что перечисление примитивно-рекурсивных или общерекурсивных функций окажется более легким делом.
Теорема 3. Для любого перечисления любого множества всюду определенных вычислимых (т.е. общерекурсивных) функций существует общерекурсивная функция не входящая в это перечисление.
Если в перечислении допускаются частичные функции, то определение В не приводит к противоречию, а лишь означает, что в точке Хв функция В(Хв) не определена.
Теорема 4. Проблема определения общерекурсивности алгоритмов неразрешима.
Не существует алгоритма В(х) такого, что для любого алгоритма Ах

Возникает естественное желание либо вообще убрать частичные алгоритмы из общей теории алгоритмов (скажем, не считать их ал-горитмами), либо ввести стандартный метод доопределения частичных алгоритмов. Однако ни то, ни другое эффективными методами сделать нельзя. В силу последней теоремы нет эффективного способа распознавать частичные алгоритмы среди множества всех алгоритмов и следовательно, предполагаемый отбор невозможен. Что касается второй идеи, для нее существует не менее убедительное опровержение:
Теорема 5. Существует такая частично-рекурсивная функция f, что никакая общерекурсивная функция g не является ее доопределением.
Следовательно, существуют частичные алгоритмы, которые нельзя доопределить до всюду определенного алгоритма.
Еще одна идея: построить язык, описывающий все всюду определенные алгоритмы и только их. Осуществить ее нельзя потому, что описания в этом языке можно упорядочить и следовательно, наличие такого языка означало бы существование полного перечисления всех всюду определенных функций, что противоречит теореме 3.
Таким образом, возникает дилемма: либо определение алгоритма должно быть достаточно общим, чтобы в число объектов, удовлетворяющих этому определению заведомо вошли все объекты, которые естетственно считать алгоритмами, либо требование об обязательной результативности сохраняется.
В первом случае этому определению будут удовлетворять частичные алгоритмы и избавиться от них конструктивными методами нельзя. Во втором случае никакую процедуру нельзя называть алгоритмом до тех пор, пока для нее не решена проблема остановки, а единого метода решения этой проблемы не существует.
Впрочем, когда речь идет об алгоритме, решающем данную задачу, теория алгоритмов обязательно требует сходимости. И только в случае, когда алгоритм решения всюду определен, соответствующая задача считается разрешимой.
Просматривая весь запас алгоритмически неразрешимых проблем, можно заметить, что все они так или иначе связаны с самоприменимостью. Понятие самоприменимости весьма далеко от алгоритмической практики, следовательно, можно предположить, что и неразрешимость в этой практике никогда не встречается.
Теорема Райса. Никакое нетривиальное свойство вычислимых функций не является алгоритмически разрешимым.
Отсюда следует, что по номеру вычислимой функции нельзя узнать, является ли эта функция постоянной, периодической, ограниченной и т.д.
Чтобы разобраться в смысле теоремы Райса, следует вспомнить, что номер хфункции f – это номер алгоритма Ах, вычисляющего f; по номеру алгоритма однозначно восстанавливается его описание, и разным номерам соответствуют разные алгоритмы.
Для функций это неверно: при xyfx и fy могут быть одной и той же функцией ( в ее классическом смысле).
Можно ли по тексту сколько-нибудь сложной программы (не запуская ее в работу) понять, что она делает ( не имея гипотез о том, что она должна делать)? В этом тексте алгоритмическим путем можно отыскать так называемые синтаксические ошибки – те или иные свойства описания алгоритма (и это делают трансляторы и компиляторы с алгоритмических языков программирования).
Хорошо известно, что в процессе отладки программ синтаксические ошибки обнаруживаются очень быстро; все неприятности связаны с анализом семантики программы, т.е. с попытками установить, что же собственно программа делает, вместо того, чтобы делать задуманное.
Мы говорили о неразрешимых проблемах внутри самой теории алгоритмов. Некоторые из них имеют вполне реальную интерпретацию в практике программирования. Неразрешимости возникают и в других областях – в теории автоматов, в синтаксическом анализе и других и с существованием их приходится считаться.
Если же важно иметь дело с разрешимой задачей, то следует четко представлять, что, во-первых отсутствие общего алгоритма, решающего данную проблему не означает, что в частном случае нельзя добиться успеха. Во-вторых, появление неразрешимости – как правило, результат черезмерной общности задачи. Задача в более общей постановке имеет больше шансов оказаться неразрешимой.
Самоприменимость МТ
Поможем написать любую работу на аналогичную тему
Рассмотрим машины Тьюринга, внешние алфавиты которых содержат символы 0,1 (наряду с другими). Для каждой машины Тьюринга Т построим Код(Т), который является (0,1)-словом, и запустим машину Т в начальной конфигурации q1Код(Т). Если машина Т останавливается (т.е. попадает в заключительное состояние) через конечное число шагов, то она называется самоприменимой, в противном случае – несамоприменимой. Существуют как самоприменимые, так и несамоприменимые машины Тьюринга. Например, несамоприменимой будет машина Т1, у которой все команды имеют вид qiaj→qiajС (в правых частях команд нет заключительного состояния), самоприменимой будет машина Т1, у которой все команды имеют вид qiaj→q0ajE (в правых частях всех команд имеется заключительное состояние). Проблема самоприменимости состоит в том, чтобы по любой машине Тьюринга Т определить, является ли она самоприменимой или нет. Будем считать, что машина Тьюринга М решает проблему самоприменимости, если для любой машины Т начальную конфигурацию q1Код(Т) она переводит в q01,
если машина Т самоприменима, и в q00, если машина Т несамоприменима.
Теорема 1. Не существует машины Тьюринга М, решающей проблему самоприменимости, т.е. проблема самоприменимости алгоритмически неразрешима.
Доказательство (от противного).
Предположим противное, т.е. пусть существует машина Тьюринга М, решающая проблему самоприместимости в указанном выше смысле. Построим новую машину М0, добавив новое состояние q0* и объявив его заключительным, а также добавив новые команды для состояния q0, которое было заключительным в М:
Рассмотрим теперь работу машины М0.
Пусть Т – произвольная машина. Если Т – самоприменима, то начальная конфигурация q1Код(Т) перейдет с помощью команд машины М через конечное число шагов в конфигурацию q01, далее применяется команда (1), и машина М0 никогда не остановится. Если Т – несамоприменима, то начальная конфигурация q1Код(Т) перейдет с помощью команд машины М через конечное число шагов в конфигурацию q00, далее применяется команда (2), и машина М0 остановится.
Таким образом, машина М0 применима к кодам самоприменимых машин Т и неприменима к кодам самоприменимых машин Т.
Теперь рассмотрим Код(М0) и применим машину М0 к начальной конфигурации q1Код(М0). Сама машина М0 является либо самоприменимой, либо несамоприменимой. Если М0 самоприменима, то по доказанному она никогда не остановится, начав с q1Код(М0), и потому она несамоприменима. Если М0 несамоприменима, то по доказанному, она останавливается через конечное число шагов, начав с q1Код(М0), и потому она самоприменима. Получили противоречие, которое является следствием допущения существования машины М0, решающей проблему самоприменимости, что и требовалось доказать.
5.3.1.2. Самоприменимость МТ
Рассмотрим машины Тьюринга, внешние алфавиты которых содержат символы 0,1 (наряду с другими). Для каждой машины Тьюринга Т построим Код(Т), который является (0,1)-словом, и запустим машину Т в начальной конфигурации q1Код(Т).
если машина Т самоприменима, и в q00, если машина Т несамоприменима.
Теорема 1. Не существует машины Тьюринга М, решающей проблему самоприменимости, т.е. проблема самоприменимости алгоритмически неразрешима.
Доказательство (от противного).
Предположим противное, т.е. пусть существует машина Тьюринга М, решающая проблему самоприместимости в указанном выше смысле. Построим новую машину М0, добавив новое состояние q0* и объявив его заключительным, а также добавив новые команды для состояния q0, которое было заключительным в М:
Рассмотрим теперь работу машины М0.
Пусть Т – произвольная машина. Если Т – самоприменима, то начальная конфигурация q1Код(Т) перейдет с помощью команд машины М через конечное число шагов в конфигурацию q01, далее применяется команда (1), и машина М0 никогда не остановится. Если Т – несамоприменима, то начальная конфигурация q1Код(Т) перейдет с помощью команд машины М через конечное число шагов в конфигурацию q00, далее применяется команда (2), и машина М0 остановится.
Таким образом, машина М0 применима к кодам самоприменимых машин Т и неприменима к кодам самоприменимых машин Т.
Теперь рассмотрим Код(М0) и применим машину М0 к начальной конфигурации q1Код(М0). Сама машина М0 является либо самоприменимой, либо несамоприменимой. Если М0 самоприменима, то по доказанному она никогда не остановится, начав с q1Код(М0), и потому она несамоприменима. Если М0 несамоприменима, то по доказанному, она останавливается через конечное число шагов, начав с q1Код(М0), и потому она самоприменима. Получили противоречие, которое является следствием допущения существования машины М0, решающей проблему самоприменимости, что и требовалось доказать.
Не распознаваемость самоприменимости машины Тьюринга
Приведем доказательство о не распознаваемости самоприменимости машины Тьюринга.
Для этого нам понадобятся следующие теоремы и определения.
Теорема 3.2.1. (о композиции машин Тьюринга). Каковы бы ни были машины Тьюринга Т1 и Т2 в алфавите А, можно построить работающую в том же алфавите такую машину Т, что для всех слов a над алфавитом А будет выполнено равенство Т(a)=Т2(Т1(a)).
Доказательство этой теоремы осуществляется просто. Внутренние состояния машин Т1 и Т2 (включая начальные состояния) переименовываются, причем в функциональной схеме машины Т1 переход в заключительное состояние заменяется переходом в начальное состояние машины Т2. При этом функциональные схемы объединяются в одну.
Теорема 3.2.2. (о двоичном моделировании машины Тьюринга) Какова бы ни была машина Т1 в алфавите А, может быть построена такая машина Т в алфавите В=
Из этой теоремы следует, что в теории машин Тьюринга вполне можно рассматривать только те машины, которые работают в двоичном алфавите. Более того, кроме двух способов задания машины Тьюринга (в виде функциональной схемы и списка команд) возможен третий способ ее записи – в виде двоичного слова.
При этом с помощью побуквенного обратимого (конструктивного) двоичного кодирования кодируются в общем случае:
– символы внешнего алфавита и алфавита внутренних состояний,
– символы, используемые при записи команд машины Тьюринга (Л, П, →,«оставаться на месте»),
– символ, фиксирующий начало и конец программы,
– символ, служащий разделителем между командами.
Подчеркнем, что сама двоичная кодировка указанных символов может осуществляться разными способами (один из способов можно найти в []). Важно лишь то, что кодирование обязательно должно быть обратимым. В этом случае двоичная запись машины Тьюринга (Т), которую далее будем обозначать, следуя [] Т ( условная запись двоичного кода символа, фиксирующего начало и конец программы), будет однозначно задавать функциональную схему машины Т.
| Заметим также, что двоичная запись машины Тьюринга однозначно определяет натуральное число. Натуральные числа, являющиеся записями машины Тьюринга называют геделевскими – по имени австрийского математика Курта Геделя, впервые в 30 годы XX века использовавшего номера объектов вместо них самих для формальных рассуждений об этих объектах. |  К.Гедель К.Гедель |
Рассматривая далее множество машин Тьюринга
Применима ли машина Тьюринга Т, заданная своей записью Т, к двоичному слову p или нет?
Еще одна известная массовая проблема теории алгоритмов – проблема самоприменимости – звучит так.
Применима ли машина Тьюринга Т, заданная своей записью Т, к своей записи Т или нет?
Очевидно, что проблема самоприменимости является частным случаем проблемы остановки. И если проблема самоприменимости алгоритмически неразрешима, то и проблема остановки относится к числу алгоритмически неразрешимых проблем.
Тот факт, что проблема самоприменимости алгоритмически неразрешима, фиксирует следующая теорема.
Теорема 3.2.3. (о нераспознаваемости самоприменимости). Не существует машины Тьюринга S, которая по записи Т определяла бы, самоприменима машина Т или нет.
Доказательство. Предположим противное и допустим, что существует машина Тьюринга S, распознающая самоприменимость. Без ограничения общности можно считать, что S(C)=1, а S(Н)=0, где C – произвольная самоприменимая машина Тьюринга, а Н – произвольная несамоприменимая машина Тьюринга.
Введем в рассмотрение машину Т1 с алфавитом внутренних состояний Q=
| Q A | q1 | q2 |
| a0 | q11Л | q21Л |
| q00 | q21Л | |
| q21Л | q21Л |
Как видно из приведенной схемы, если первая буква исходного слова a есть 0, то Т1(a)=a. Если же исходное слово a пусто или начинается с 1, то Т1 неприменима к слову a, Т1(a)=1111…
Определим теперь новую машину Тьюринга S1 как композицию машины S и машины Т1, полагая S1(a)=Т1(S(a)).
Предположим далее, что машина S1 самоприменима. Это означает, что S1 – запись самоприменимой машины и по определению машины S S(S1)=1. В то же время,
что означает несамоприменимость машины S1. Противоречие налицо.
Предположение о том, что машина S1 несамоприменима, влечет за собой (по определению машины S) соотношение S(S1)=0. Но по определению машины S1 S1(S1)=Т1(S(S1))=Т1(0)=0, что означает самоприменимость машины S1.
Вновь получаем противоречие.
Иными словами, предположение о существовании машины S, распознающей самоприменимость приводит к противоречию.
Следствие. Проблема остановки алгоритмически неразрешима.
Проблема самоприменимости в теории алгоритмов явилась первой алгоритмически неразрешимой проблемой, от которой отталкивались в дальнейших исследованиях.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
