Проверка второго закона ньютона на машине атвуда лабораторная работа

Проверка второго закона Ньютона на машине Атвуда

ЦЕЛЬ: установить зависимость ускорения системы от действующей силы; определить из полученной зависимости массу системы.

ОБОРУДОВАНИЕ: экспериментальная установка FRM ; электронный секундомер с фотоэлектрическими датчиками, линейка.

ОСНОВЫ ТЕОРИИ

где р = m v  импульс тела,

Для малых скоростей массу можно считать постоянной и вынести из-под знака дифференциала:

Масса. Опыт показывает, что одинаковые воздействия вызывают у разных тел различные изменения скорости. Одному и тому же телу различные силы сообщают различные ускорения. Однако отношение силы к ускорению для каждого тела всегда равно одной и той же величине:

Следовательно, масса является количественной мерой инертности тел. Под инертностью понимается свойство тел противиться изменению скорости. Отношение F/a = const справедливо только при достаточно малых скоростях.

где m 0 – константа, называемая массой покоя (масса тела при при v = 0),

с  скорость света в вакууме.

Определенная в формуле (5) масса тела m является функцией его скорости:

При v « c масса тела мало отличается от m 0 и соотношение (4) можно считать справедливым. Уравнения (1) и (3) формально эквивалентны. Однако это имеет место только при малых скоростях движения. Оказалось, что в релятивисткой динамике уравнения (1) и (2) остаются справедливыми, если массу определять в соответствии с выражением (6). Соотношение (3) при больших скоростях перестает быть справедливым.

МЕТОДИКА ЭКСПЕРИМЕНТА

Рис. 1. Машина Атвуда.

Запишем второй закон Ньютона для груза m 1 :

Спроецируем его на ось x 1 :

Аналогично для груза m 2 :

В проекциях на ось x 2 : :

В силу принятых выше допущений

Складывая уравнения (7) и (8), получим:

Введем обозначения для суммарной массы системы:

и эффективной силы, численно равной разности сил тяжести грузов:

Тогда формула (9) примет вид:

с коэффициентом пропорциональности, обратным полной массе системы:

Тогда выражение (10) примет вид:

Логическая схема эксперимента

Для проверки пропорциональности между a и F каждая из этих величин должна быть определена независимым способом.

ВЫПОЛНЕНИЕ РАБОТЫ

1. Определите взвешиванием массы грузов и перегрузков.

2. Установите левый груз в крайнее нижнее положение.

3. Поместите на правый груз большой перегрузок, на левый груз  все маленькие перегрузки.

4. Отпустите левый груз и измерьте время движения грузов, а также путь, пройденный одним из них.

5. Перенося по одному перегрузку с левого груза на правый, повторяйте опыт до тех пор, пока на левом грузе не останется ни одного перегрузка. Результаты измерений занесите в таблицу.

Источник

Лабораторная работа 1 «Проверка основных законов механикина машине Атвуда.»

Лабораторная работа 1.1

“Проверка основных законов механикина машине Атвуда.”

Цель работы: Изучение законов равноускоренного движения и проверка второго закона Ньютона.

Задание к работе:

Теоретическое введение

Механика изучает простейшую форму движения материи – механическое движение, состоящее в перемещении тел или их частей друг относительно друга, и включает в себя разделы: кинематика, статика, динамика.

Кинематика изучает движение тел вне зависимости от причин, обуславливающих это движение; динамика – характер и причины движения в их взаимосвязи; статика – законы равновесия тел.

Скорость – вектор, её направление совпадает с направлением перемещения. В случае неравномерного движения точки тела за равные промежутки времени проходят неодинаковые пути. Поэтому отношение пути ко времени, за который пройден путь, дает лишь среднее значение скорости:

Чтобы получить значение скорости в данный момент времени, необходимо рассмотреть это отношение при бесконечно малом перемещении ΔS:

Вектор скорости направлен по касательной к траектории движения, также в сторону перемещения.

Движение называется переменным, если величина скорости меняется во времени. Для характеристики быстроты изменения скорости вводится ускорение:

Направление вектора совпадает с вектором изменения скорости. Если известен закон изменения ускорения во времени, можно найти скорость тела в любой произвольный момент времени:

и путь, пройденный телом за это время:

При равнопеременном движении (W=±Const)

Для равноускоренного движения (W>0) из состояния покоя (V₀=0)

Величина и направление ускорения тела определяются величиной и направлением действующей на него силы.

Сила – векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Согласно второму закону Ньютона в результате воздействия тело получает ускорение

где F – действующая на тело сила, m – масса тела.

Если учесть, что , то второй закон Ньютона можно записать в дифференциальной форме:

или, учитывая, что ,

где — импульс тела. Быстрота изменения импульса тела с течением времени совпадает с приложенной к телу силой.

Друга эквивалентная форма записи второго закона Ньютона имеет вид:

где, — импульс силы за время dt.

Бесконечно малое изменение импульса тела по величине и направлению равно бесконечно малому импульсу силы.

Установка включает в себя машину Атвуда, электронный блок и набор перегрузов.

Установка состоит из основания 2, на вертикальной стойке 1 которого размещены верхний 5, средний 4, и нижний 3 кронштейны. На верхнем кронштейне 5 крепится блок, через который перекинута нить с грузами 6 одинаковой массы. Электромагнит 7 с помощью фрикциона удерживает систему с грузами в неподвижном состоянии. На среднем кронштейне 4 установлен фотодатчик 8, подающий сигнал окончания счёта времени движения грузов. Средний кронштейн имеет индекс, положение которого совпадает с оптической осью фотодатчика. На площадке нижнего кронштейна 3 имеется амортизатор для остановки груза. Кронштейны 3 и 4 могут свободно перемещаться и фиксироваться на вертикальной стойке 1 по всей её свободной длине. По миллиметровой шкале 9 определяют начальное и конечное положение грузов и пройденный ими путь. Начальное положение определяют визуально по нижнему срезу груза, конечное – по индексу среднего кронштейна 4.

На передней панели электронного блока 10 имеются индикаторы «ПЕРИОД», «ВРЕМЯ», кнопки управления: «СБРОС», «ПУСК», «СТОП» и тумблер «СЕТЬ» с помощью которого подаётся питание на блок 10. При нажатии на кнопку «СБРОС» на цифровых индикаторах «ПЕРИОД» и «ВРЕМЯ» устанавливаются нули. Если нажать на кнопку «ПУСК», то опускается подвижная часть с грузами физического прибора, таймер отсчитывает время и при пересечении правым грузом оптической оси фотодатчика счёт времени прекращается. При нажатии на кнопку «СТОП» подвижная часть тормозится электромагнитом 7 и прекращается счёт периодов и длительности. Для нового запуска необходимо нажать кнопку «СБРОС», а затем «ПУСК».

Масса грузов С₁ и С₂ может быть увеличена добавочными перегрузками.

Принцип работы установки состоит в том, что когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если 6на один из грузов положить перегрузок массой Δm, система выходит из равновесия и начинает двигаться равноускоренно. На каждый груз действует две силы: сила тяжести и сила натяжения нити под действием которых грузы движутся. Предполагая, что нити и блок невесомы, нить нерастяжима, а сила трения в системе мала, получили, что ускорения обоих грузов будет одинаковы по величине, а натяжение нити одинаково справа и слева.

где W – ускорение груза, T – сила натяжения нити, g – ускорение свободного падения, m – масса груза, Δm– масса перегрузка.

Решение этих уравнений даёт величину ускорения:

где — масса всей системы грузов. Отсюда видно, что система будет двигаться с ускорением, меньшим, чем ускорение свободного падения. Увеличивая массу перегрузка Δm, можно увеличить ускорение системы. Если перегрузок Δm, убрать во время движения, то дальнейшее движение системы бедет происходить с постоянной скоростью, равной скорости в момент снятия перегрузка.

Сила, приводящая систему грузов в движение равна:

Если, не меняя массы всей системы ( M=Const), увеличить Δm (например, перекладывать перегрузок Δm, с груза С₁ на С₂), сила, действующая на систему, увеличится; увеличится и ускорение грузов. Однако при любых Δm, должно

выполняться соотношение:

что свидетельствует о выполнении закона Ньютона.

Следует убедиться, что движение системы при фиксированной массе переурузка Δm равняется равноускоренным. Для этого нужно экспериментально проверить выполнение зависимости:

Из этого соотношения ясно, что в осях координат и прямая , проходящая через начало координат, соответствует равноускоренному движению.

Важно выяснить подтверждается ли на опыте зависимость времени падения от массы перегрузка Δm.

В осях координат функция является уравнением прямой, по тангенсу угла наклона которой к оси абсцис можно определить ускорение свободного падения.

Источник

Краткие теоретические сведения

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Сибирский государственный аэрокосмический университет

Имени академика М. Ф. Решетнева»

(СибГАУ)

ПРОВЕРКА ВТОРОГО ЗАКОНА ДИНАМИКИ

НА МАШИНЕ АТВУДА

Методические указания к выполнению

лабораторной работы 2

Красноярск 2013

Лабораторная работа 2

ПРОВЕРКА ВТОРОГО ЗАКОНА МЕХАНИКИ

НА МАШИНЕ АТВУДА

Цель работы: проверка основного закона динамики посту­пательного движения.

Приборы и принадлежности: машина Атвуда, набор грузов и перегрузков, секундомер.

Краткие теоретические сведения

Динамика раздел механики изучающий движения тел в связи с теми причинами (взаимодействия между телами), которые обуславливают тот или иной характер движения. Мерой взаимодействия тел является сила. Классическая (ньютоновская) динамика опирается на три закона описывающие взаимодействия тел (законы Ньютона).

Первый закон Ньютона определяет границы применимости остальных законов и связан с понятием инертности, введенным в физику Г. Галилеем. Первый закон Ньютона (закон инерции) гласит: существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или прямолинейного равномерного движения, до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.

Первый закон Ньютона показывает, что состояние покоя или прямолинейного равномерного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство всех тел, называемое инертностью. Но инерция наблюдается не во всякой системе отсчета. Система отсчета в механике это совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение. Для количественного описания движения, тела образующие систему отсчета, связываются с системой координат, и выбирается способ отсчета времени (часы). Те системы, где наблюдается инерция (выполняется первый закон Ньютона) называют инерциальными системами, где не наблюдается – неинерциальными. Рассмотрим инерциальные и неинерциальные системы отсчета на примере описания движения шара лежащего на гладком полу каюты корабля. Когда корабль движется прямолинейно и равномерно, сумма сил действующих на шар равна нулю. Шар будет покоиться, в системе отсчета связанной с кораблем, пока на него не начнут воздействовать другие тела. В системе отсчета связанной с Землей шар движется прямолинейно и равномерно со скоростью корабля, пока на него не начнут воздействовать другие тела. В обеих этих системах при движении шара выполняется первый закон Ньютона, следовательно, обе системы – инерциальные. Теперь пускай корабль начнет менять свою скорость, например, тормозить. В этом случае шар не будет находиться в покое и начнет движение по полу каюты. В системе отсчета связанной с Землей шар продолжает двигаться прямолинейно и равномерно, стремясь и дальше сохранять свою скорость. В этой системе выполняется первый закон Ньютона, и система является инерциальной. В системе отсчета связанной с кораблем, шар приобретает ускорение без воздействия на него других тел. В такой системе не выполняется первый закон Ньютона и она будет неинерциальной.

Можно также сделать вывод, что инерциальными будут все системы, которые покоятся или движутся прямолинейно и равномерно относительно инерциальной системы. На основе этого Г. Галилей сформулировал свой Принцип относительности:

1. Ни какими механическими опытами нельзя установить покоится инерциальная система или она движется прямолинейно и равномерно.

2. Все инерциальные системы равноправны.

3. Законы классической механики во всех инерциальных системах отсчета имеют один и тот же вид, т.е. они инвариантны к преобразованиям Галилея (переходу от одной инерциальной системы отсчета к другой).

Замечание: строго говоря, система отсчета жестко связанная с Землей (геоцентрическая, лабораторная система отсчета) не является инерциальной системой, т.к. Земля движется с ускорением из-за вращения вокруг своей оси и вращения вокруг Солнца. Но ускорения, вызванные этим вращением крайне малы. Для большинства задач систему отсчета связанную с Землей можно считать инерциальной системой.

Чтобы вывести тело из состояния прямолинейного равномерного движения необходимо, чтобы на материальную точку начала действовать сила. Второй закон Ньютона в наиболее общей формулировке гласит: скорость изменения импульса материаль­ной точки равна действующей на нее силе

,

где векторная величина

,

численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки. Второй закон Ньютона, в этой форме записи, справедлив не только в классической механике, но и релятивисткой механике.

Перепишем второй закон Ньютона, расписав импульс

.

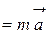
Выразив ускорение, получим другую форму записи второго закона Ньютона: ускорение, приобретаемое материальной точкой, пропорцио­нально вызывающей его силе, совпадает с нею по направлению и об­ратно пропорционально массе материальной точки

.

Масса выступает мерой инерциальных свойств материальной точки. Различие в массе тел приводит к тому, что при действии одной и той же силы на различные тела их ускорение оказывается различным.

Сила, с которой одна материальная точка действует на другую, зависит только от координат и скоростей только этих двух материальных точек. Присутствие других материальных точек на эту силу не влияет. Это свойство называется законом независимости действия сил или законом парности взаимодействия. Из закона парности следует, что если на тело действует несколько сил, под 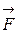понимают векторную сумму сил, действующих на тело (равнодействующую силу)

,

.

Из закона парности взаимодействия вытекает и третий закон Ньютона: силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

,

где — сила, действующая на первую материальную точку со сторо­ны второй; — сила, действующая на вторую материальную точку со
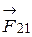
стороны первой. Эти силы приложены к разным материальным точкам (телам) и являются силами одной природы.

Описание установки

В лаборатории механики машина Атвуда представлена на двух установках: настенной (рис.2а) и настольной (рис 2б). Обе установки имеют одни и те же основные узлы и их различия несущественны при выполнении данной работы. Данная лабораторная работа может выполняться на любой из лабораторных установок.

Установка настенная (Рис. 2а) состоит из длинной, вертикальной, разделенной на сантиметры рейки, на верхнем конце которой укреплен неподвижный блок, вращающийся вокруг горизонтальной оси. Через блок перекинута нить, на концах которой подвешены два одинаковых груза. Блок управления состоит из электромагнита с ключом К₁, и секундомера с ключом К₂. Секундомер включается ключом в момент начала движения системы и выключается автоматически при соприкосновении груза к полке D.

Рис. 2а	Рис. 2б

Установка настольная (Рис. 2б) отличается тем, что шкала нанесена на вертикальной штанге, а не на рейке. На штанге крепятся кронштейны. Электромагнит, удерживающий систему в состоянии покоя, установлен на верхнем кронштейне. Верхний и средний кронштейны можно перемещать по штанге и фиксировать в любом положении. Это дает возможность изменять длину пути равноускоренного и равномерного движений.

Блок управления содержит кнопки «Сеть», «Пуск», «Сброс» и цифровой секундомер. При нажатии кнопки «Пуск» секундомера происходит отключение электромагнита, груз опускается, фотоэлектрический датчик на среднем кронштейне, фиксирующий начало движения и автоматически включает секундомер. На среднем кронштейне может быть закреплено кольцо, не используемое в данной лабораторной работе (оно используется при выполнении лаб. работы №12).

На неподвижном нижнем кронштейне установлены: приемный столик и еще один фотоэлектрический датчик, фиксирующий окончание движения системы и автоматически выключающий секундомер.

Регулировочные опоры в нижней части установки используют для регулировки положения экспериментальной установки на лабораторном столе. Перед проведением опытов прибор следует установить в строго вертикальное положение с помощью ножек–винтов.

Источник