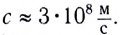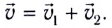Пусть совпадает с модулем перемещения при прямолинейном движении автомобиля
Физика. 8 класс
Поступательным является движение:
машины по автомагистрали
человека, сидящего в кабинке фуникулёра
Земли вокруг своей оси
весла при гребле на байдарке
Самолёт можно рассматривать как точку при расчёте:
пути, пройденного им за 1 ч
скорости его движения
давления, оказываемого им на поверхность
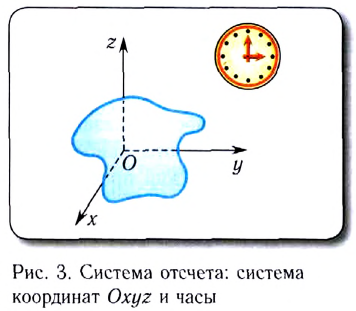
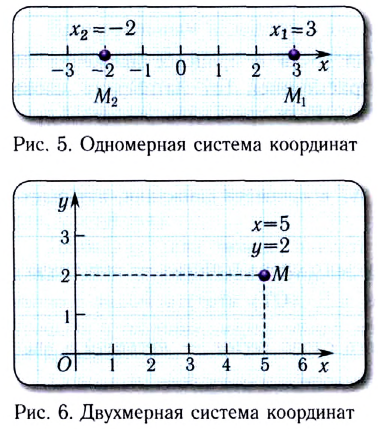
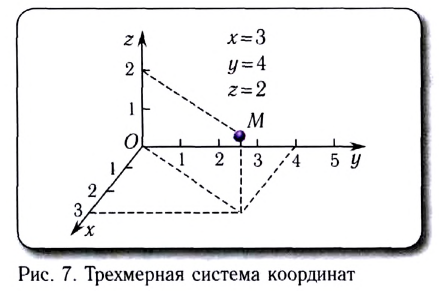
Для описания движения вертолёта необходимо использовать:
одномерную систему координат
двумерную систему координат
трёхмерную систему координат
Пусть совпадает с модулем перемещения при:
прямолинейном движении автомобиля
движении автомобиля по горному серпантину
движении белки в колесе
равномерном движении велосипедиста по стадиону
На рисунке показана траектория движения катера. Модуль перемещения катера равен: м.
Лыжник движется равномерно из точки с координатой –150 м со скорость 7 м/с. Его движение описывается уравнением:
Определите, какие из приведённых величин являются скалярными, а какие векторными. Поместите табличку с названием физической величины в соответствующую группу.
Скалярные величины
Векторные величины
Восстановите формулу скорости равномерного прямолинейного движения.
НАШИ ПАРТНЁРЫ
© Государственная образовательная платформа «Российская электронная школа»
Тренировочный модуль
Поступательным является движение:
весла при гребле на байдарке
машины по автомагистрали
человека, сидящего в кабинке фуникулёра
Земли вокруг своей оси
Тренировочный модуль
Самолёт можно рассматривать как точку при расчёте:
пути, пройденного им за 1 ч
давления, оказываемого им на поверхность
скорости его движения
Тренировочный модуль
Для описания движения вертолёта необходимо использовать:
двумерную систему координат
одномерную систему координат
трёхмерную систему координат
Тренировочный модуль
Пусть совпадает с модулем перемещения при:
движении автомобиля по горному серпантину
прямолинейном движении автомобиля
равномерном движении велосипедиста по стадиону
движении белки в колесе
Тренировочный модуль
На рисунке показана траектория движения катера. Модуль перемещения катера равен: м.
Тренировочный модуль
Лыжник движется равномерно из точки с координатой –150 м со скорость 7 м/с. Его движение описывается уравнением:
Тренировочный модуль
Определите, какие из приведённых величин являются скалярными, а какие векторными. Поместите табличку с названием физической величины в соответствующую группу.
Тест 1 к разделу «Механика»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Тест к разделу «Механика»
Тест №1 Тема. Кинематика
1. Перемещение – это:
1)векторная величина; 2) скалярная величина; 3) может быть и векторной и скалярной величиной; 4) правильного ответа нет.
2.Модуль перемещения при криволинейном движении в одном направлении:
1) равен пройденному пути; 2) больше пройденного пути; 3) меньше пройденного пути ; 4) правильного ответа нет.
3. При прямолинейном движении скорость материальной точки направлена:
1) туда же, куда направлено перемещение ; 2) против направления перемещения; 4) независимо от направления перемещения;
4. При криволинейном движении мгновенная скорость материальной точки в каждой точке траектории направлена:
1) по траектории ; 2) по касательной к траектории в этой точке ; 3) по радиусу кривизны траектории.
5. Перемещением движущейся точки называют…
1) …длину траектории; 2) пройденное расстояние от начальной точки траектории до конечной; 3)… направленный отрезок прямой, соединяющий начальное положение точки с его конечным ; 4) …линию, которую описывает точка в заданной системе отсчета.
6. Средняя скорость характеризует:
1) равномерное движение; 2) неравномерное движение;
7. Физическая величина, равная отношению перемещения материальной точки к физически малому промежутку времени, в течение которого произошло это перемещение, называется
1) средней скоростью неравномерного движения материальной точки; 2) мгновенной скоростью материальной точки; 3) скоростью равномерного движения материальной точки.
8. Направление ускорения всегда совпадает с:
1) направлением скорости; 2) направлением перемещения; 3) направлением вектора изменения скорости.
1) физическая величина, равная отношению изменения скорости к тому промежутку времени, за который это изменение произошло; 2) физическая величина, равная отношению изменения скорости к тому физически малому промежутку времени, за которое это изменение произошло; 3) физическая величина, равная отношению перемещения ко времени.
10. Проекция ускорения на координатную ось может быть:
1) только положительной; 2) только отрицательной ; 3) и положительной, и отрицательной, и равной нулю.
11. В каком случае модуль ускорения больше?
1) тело движется с большой постоянной скоростью; 2) тело быстро набирает или теряет скорость; 3) тело медленно набирает или теряет скорость.
12.Два поезда движутся навстречу друг другу по прямолинейному участку пути. Один из них движется ускоренно, второй замедленно. Их ускорения направлены:
1) в одну сторону ; 2) в противоположные стороны; 3) однозначно об их направлениях нельзя сказать.
1) 0,25с; 2) 2с; 3) 100 с ; 4) 4с.
14. При подходе к станции поезд уменьшил скорость на 10м/с в течение 20с. С каким ускорением двигался поезд?
15. Автомобиль, трогаясь с места, движется с ускорением 3м/с2. Через 4с скорость автомобиля будет равна:
1)12 м/с ; 2) 0,75 м/с; 3) 48 м/с ; 4) 6 м/с.
Тема: Законы Ньютона
16.Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают по направлению?
1)сила и ускорение ; 2) сила и скорость; 3) сила и перемещение; 4) ускорение и перемещение.
17.Какие силы в механике сохраняют свое значение при переходе из одной инерциальной системы в другую?
1) силы тяготения, трения, упругости; 2) только сила тяготения; 3) только сила упругости; 4) только сила трения.
18. Равнодействующая сила – это:
1) сила, действие которой заменяет действие всех сил, действующих на тело; 2) сила, заменяющая действие сил, с которыми взаимодействуют тела.
19. Равнодействующая всех сил, действующих на тело, равна нулю. Какова траектория движения этого тела?
1) парабола; 2) окружность ; 3) прямая ; 4) эллипс.
20. В инерциальной системе отсчета F сообщает телу массой m ускорение a. Как изменится ускорение тела, если массу тела и действующую на него силу уменьшить в 2 раза?
21. После открытия парашюта парашютист под действием силы тяжести и силы сопротивления воздуха двигался вниз с ускорением, направленным вверх. Как станет двигаться парашютист, когда при достижении некоторого значения скорости равнодействующая силы тяжести и силы сопротивления воздуха окажется равной нулю?
1) равномерно и прямолинейно вверх; 2) равномерно и прямолинейно вниз; 3) с ускорением свободного падения вниз; 4) будет неподвижным.
22. Закон инерции открыл
1) Демокрит; 2) Аристотель; 3) Галилей ; 4) Ньютон.
23. Третий закон Ньютона описывает:
1) действие одного тела на другое; 2) действие одной материальной точки на другую; 3) взаимодействие двух материальных точек.
24. Локомотив сцеплен с вагоном. Сила, с которой локомотив действует на вагон, равна силам, препятствующим движению вагона. Другие силы на движение вагона не влияют. Систему отсчета, связную с Землей, считайте инерциальной. В этом случае:
1) вагон может только покоится; 2) вагон может только двигаться с постоянной скоростью; 3) вагон движется с постоянной скоростью или покоится ; 4) вагон движется с ускорением.
25. Яблоко массой 0,3 кг падает с дерева. Выберите верное утверждение
1) яблоко действует на Землю силой 3Н, а Земля не действует на яблоко; 2) Земля действует на яблоко с силой 3Н, а яблоко не действует на Землю; 3) яблоко и Земля не действуют друг на друга; 4) яблоко и Земля действуют друг на друга с силой 3 Н.
1) 32 кг; 2) 0,5кг; 3) 2 кг ; 4) 20кг.
27.Сила тяги ракетного двигателя первой отечественной экспериментальной ракеты на жидком топливе равнялась 660Н. Стартовая масса ракеты была равна 30кг. Какое ускорение приобретала ракета во время старта?
28. Скорость лыжника при равноускоренном спуске с горы за 4с увеличилась на 6м/с. Масса лыжника 60кг. Равнодействующая всех сил, действующих на лыжника, равна
29. Материальная точка массой 1кг движется под действием двух взаимно перпендикулярных сил 8Н и 6Н. Ускорение точки равно
30. Какая из физических характеристик не меняется при переходе от одной инерциальной системы отсчета к другой?
1) ускорение ; 2) перемещение; 3) траектория; 4) кинетическая энергия.
Тема. Силы в природе
31.Закон всемирного тяготения позволяет рассчитать силу взаимодействия двух тел, если
1)тела являются телами Солнечной системы; 2) массы тел одинаковы; 3) известны массы тел и расстояние между их центрами; 4 ) известны массы тел и расстояние между ними, которое много больше размеров тел.
32.Согласно закону Гука сила натяжения пружины при растягивании прямо пропорциональна
1) ее длине в свободном состоянии; 2) ее длине в натянутом состоянии ; 3) разнице между длиной в натянутом и свободном состояниях ; 4) сумме длин в натянутом и свободном состояниях.
33. Спортсмен совершает прыжок с шестом. Сила тяжести действует на спортсмена
1)только в течение того времени, когда он соприкасается с поверхностью Земли; 2) только в течение того времени, когда он сгибает шест в начале прыжка; 3) только в течение того времени, когда он падает вниз после преодоления планки; 4) во всех этих случаях.
1) свойство тела; 2) физическая величина ; 3) физическое явление.
1) гравитационным взаимодействием; 2) электромагнитным взаимодействием; 3) и гравитационным, и электромагнитным взаимодействием.
36. Вдоль границ соприкосновения тел направлены силы:
1) вязкого трения; 2) сухого трения ; 3) и сухого, и вязкого трения.
37. При сухом трении максимальная сила трения покоя:
1) больше силы трения скольжения; 2) меньше силы трения скольжения; 3) равна силе трения скольжения.
38. Сила упругости направлена:
1 ) против смещения частиц при деформации; 2) по направлению смещения частиц при деформации; 3) о ее направлении нельзя ничего сказать.
39.Как изменяются масса и вес тела при его перемещении с экватора на полюс Земли?
1) масса и вес тела не изменяются ; 2) масса тела не изменяется, вес увеличивается; 3) масса тела не изменяется, вес уменьшается; 4) масса и вес тела уменьшаются.
40. Космический корабль после выключения ракетных двигателей движется вертикально вверх, достигает верхней точки траектории и затем движется вниз. На каком участке траектории в корабле наблюдается состояние невесомости? Сопротивление воздуха пренебрежимо мало.
1) только во время движения вверх; 2) только во время движения вниз; 3) только в момент достижения верхней точки траектории ; 4) во время всего полета с неработающими двигателями.
41. Космонавт на Земле притягивается к ней с силой 700Н. С какой приблизительно силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса в 2 раза, а а масса – в 10 раз меньше, чем у Земли?
1) 70Н; 2) 140 Н; 3) 210 Н ; 4) 280Н.
42. Под действием силы 3Н пружина удлинилась на 4 см, а под действием силы 6Н удлинилась на 8см. Чему равен модуль силы, под действием которой удлинение пружины составило 6 см?
1) 3,5Н; 2) 4Н; 3) 4,5 Н ; 4) 5Н.
43. При скольжении бруска массой 5кг по горизонтальной поверхности сила трения равна 10Н. Чему равен коэффициент трения скольжения для этой пары тел?
1) 0,5; 2 ) 0,2; 3) 2; 4) 5.
44. Автомобиль массой 1000кг едет по выпуклому мосту с радиусом кривизны 40м. какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали состояние невесомости?
1) 0,05м/с; 2) 20м/с ; 3) 25 м/с; 4) 400м/с.
45. Расстояние между центрами двух шаров равно 1м, масса каждого шара 1 кг. Сила всемирного тяготения между ними примерно равна
Содержание:
Равномерное прямолинейное движение:
Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?
Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?
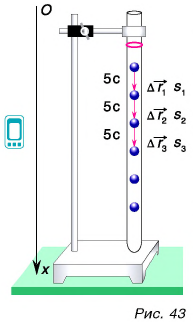
Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за
Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.
В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: 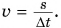
Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:
Из равенства (1) следует, что скорость 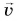
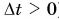
Отношение 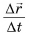
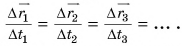
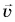
Из формулы (1) легко найти перемещение:
и путь 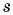
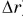
А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени 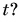
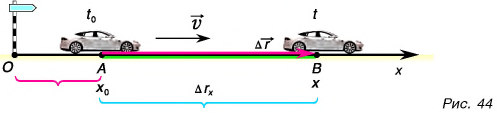
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время 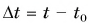
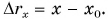
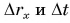
Приняв 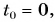
Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.
Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.
Для любознательных:
Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.
Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!
Главные выводы:
Пример решения задачи:
Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением 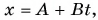
Определите: 1) проекцию скорости лодки 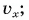
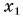
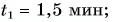
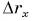
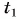
Решение
Сделаем рисунок к задаче.
По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив 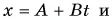
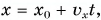
Найдем
Из рисунка 49: проекция перемещения
Ответ:
Графическое представление равномерного прямолинейного движения
Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.
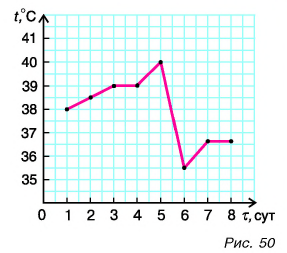
Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.
В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.
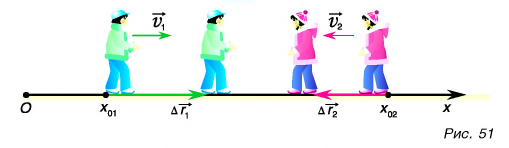
Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши 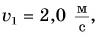
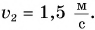
Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при 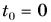
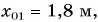
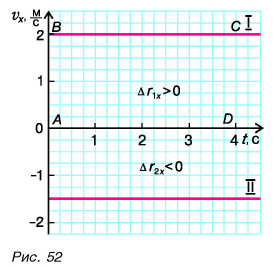
Построим графики зависимости проекции скорости 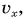
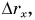
График проекции скорости
Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: 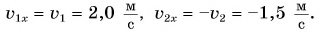
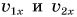
Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.
График проекции перемещения
Проекция перемещения 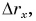
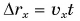
Зависимость проекции перемещения от времени для Леши 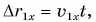
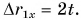
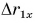
Для Тани 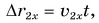
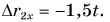
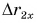
Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.
График пути
Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: 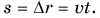
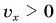
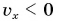
Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.
График координаты
Его называют также графиком движения.
По формуле 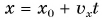
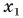
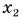
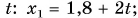
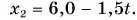
Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.
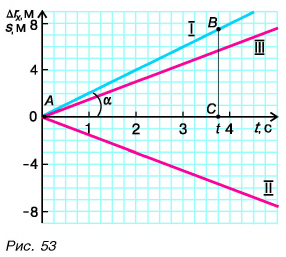
По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.
Что еще можно определить по графикам?
По графику проекции скорости можно найти проекцию перемещения и пройденный путь
Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна 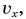
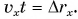
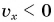
Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.
По углу наклона графика проекции перемещения можно оценить скорость движения
Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.
Главные выводы:
Для равномерного прямолинейного движения:
Пример №1
Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью 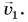
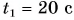
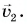
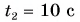
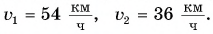
Решение
Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.
В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:
Найдем координату 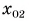
Кинематический закон движения велосипедиста имеет вид:
Расстояние между мотоциклистом и велосипедистом через время 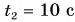
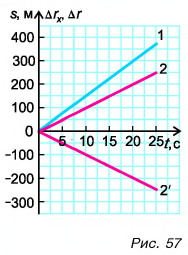
Пример №2
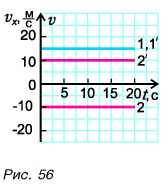
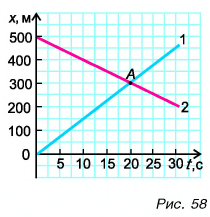
Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости 
Графиками пути s, проекции 
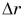
Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).
Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая 
Графики координат представлены на рисунке 58. Они выражают зависимости 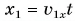
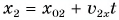
Ответ:
Прямолинейное равномерное движение и скорость
Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.
Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.
При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:
Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено:
Если скорость 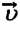
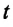
При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:
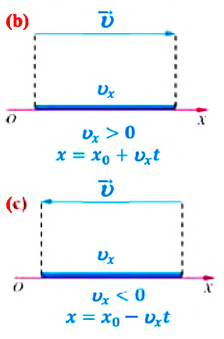
Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:
Можно получить формулу для вычисления координаты точки 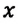
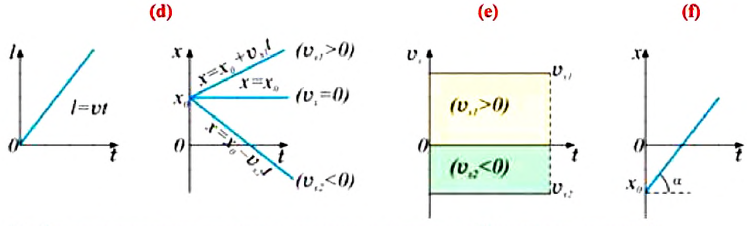
Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).
Из формулы (1.5) определяется выражение для проекции скорости:
Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.
График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f):
Пример №3
Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста 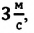
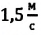
Определите: а) координату и время 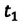
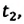
a) При решении задачи соблюдается следующая последовательность действий:
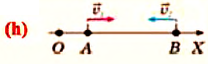
I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).
II действие. Уравнение движения записывается в общем виде:
III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде:
IV действие. Координаты велосипедистов при встрече равны: 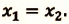
V действие. Для определения координат 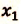
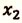
Так как 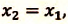
b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:
c) Время 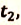
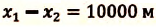
Скорость при равнопеременном прямолинейном движении
Из формулы (1.14) видно, что если известны ускорение 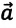
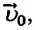
или ее проекцию на ось
Если начальная скорость равна нулю 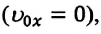
Перемещение при равнопеременном прямолинейном движении
Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком 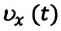
На приведенных графиках — это заштрихованная фигура трапеции (см: с):
или в векторной форме:
Если в последнюю формулу вместо 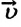
обобщенную формулу перемещения для равнопеременного движения:
Таким образом, формула проекции перемещения (например, на ось 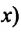
а формула координаты:
(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя 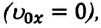
Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени 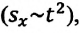
В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время 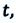
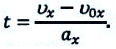
Это выражение подставляется в формулу (1.21):
После простых преобразований получаем:
Для проекции конечной скорости получаем: 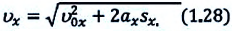
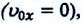
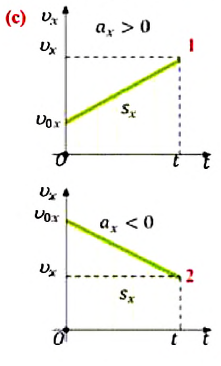
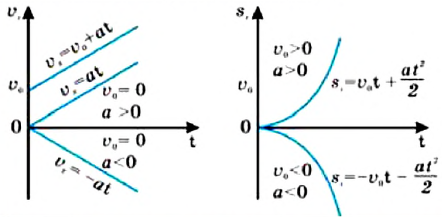
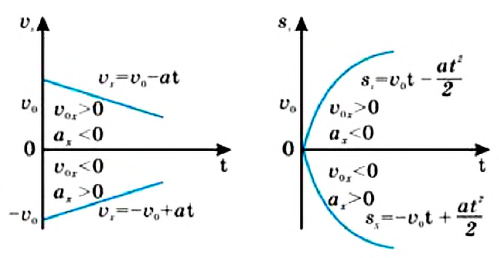
Равноускоренное и равнозамедленное движения
Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.
При равноускоренном движении векторы 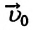
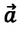
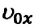
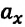
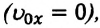
В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.


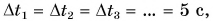



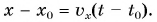




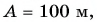
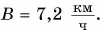
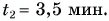


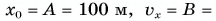
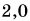
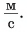
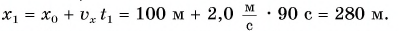
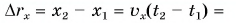
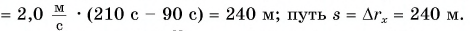
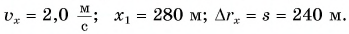
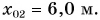
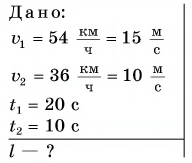

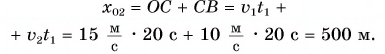
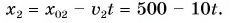
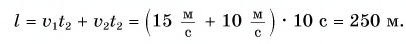
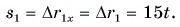
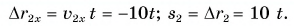
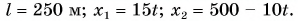
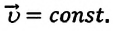
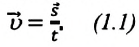
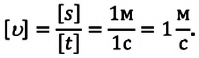

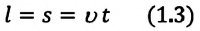
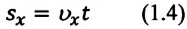
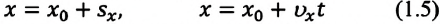
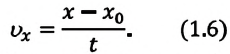
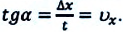
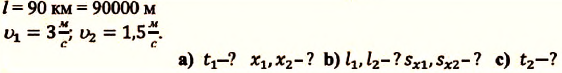
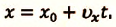
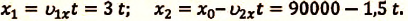
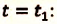
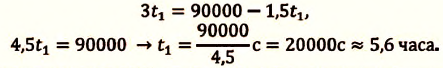
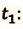
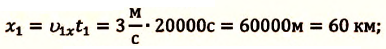
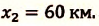
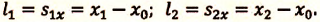
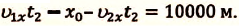
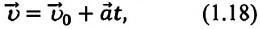
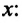
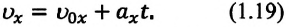

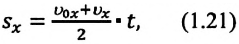
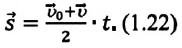
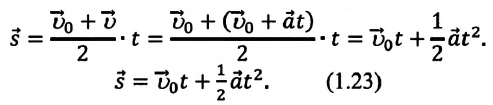
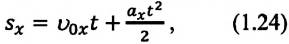
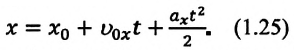
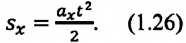
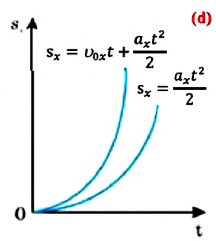
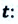
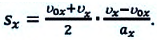

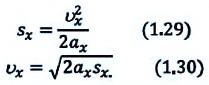
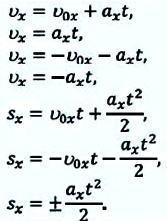
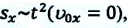 то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени: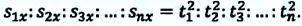
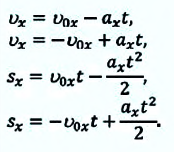
 — подъемная машина).
— подъемная машина).
 — движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова
— движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова 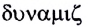 — сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова
— сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова 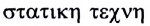 — искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.
— искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.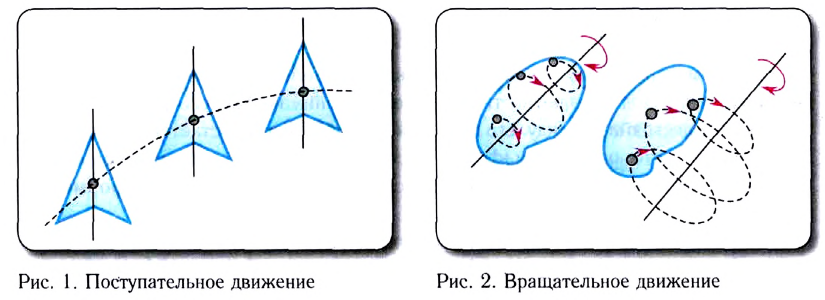
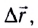 направленный из точки, заданной радиус-вектором
направленный из точки, заданной радиус-вектором 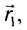 где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором
где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором 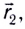 где МТ находится в рассматриваемый момент времени (рис. 4):
где МТ находится в рассматриваемый момент времени (рис. 4):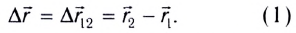
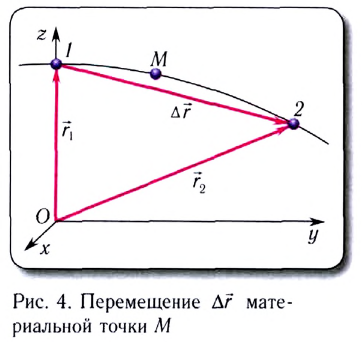
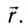
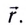 всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением
всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением 
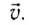
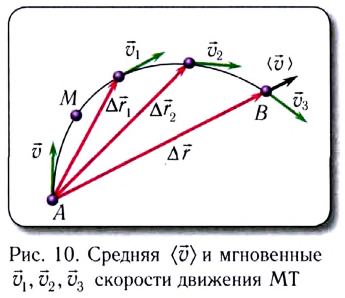
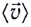 движения как отношение перемещения
движения как отношение перемещения 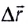 тела к промежутку времени
тела к промежутку времени 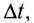 за который это перемещение произошло (рис. 10):
за который это перемещение произошло (рис. 10):
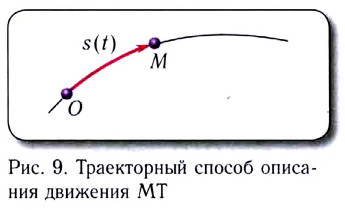
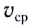 называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени
называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени 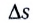 его прохождения:
его прохождения:
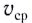 в отличие от средней скорости
в отличие от средней скорости 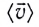 является скалярной величиной.
является скалярной величиной.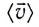 характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.
характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.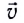 — это скорость тела (МТ), равная производной перемещения по времени:
— это скорость тела (МТ), равная производной перемещения по времени:
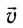 в любой точке траектории направлен по касательной к ней (см. рис. 10).
в любой точке траектории направлен по касательной к ней (см. рис. 10).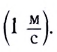
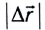 равен пройденному пути s. Скорость
равен пройденному пути s. Скорость 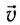 равномерного движения равна отношению перемещения тела
равномерного движения равна отношению перемещения тела 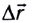 ко времени
ко времени 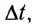 за которое это перемещение произошло:
за которое это перемещение произошло:
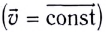 и равна средней скорости
и равна средней скорости 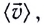 определяемой выражением (2).
определяемой выражением (2).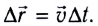 Вследствие того, что
Вследствие того, что 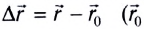 — радиус-вектор, задающий положение МТ в начальный
— радиус-вектор, задающий положение МТ в начальный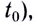 получаем кинематическое уравнение движения в векторном виде
получаем кинематическое уравнение движения в векторном виде
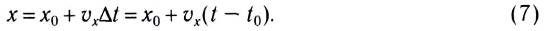
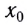 — координата тела (МТ) в начальный момент времени
— координата тела (МТ) в начальный момент времени  Если начальный момент времени
Если начальный момент времени 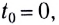 уравнение принимает вид
уравнение принимает вид
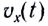 от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси
от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси 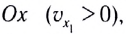 а 2 — в отрицательном
а 2 — в отрицательном 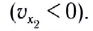 Площади
Площади 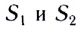 закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей
закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей 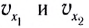 за промежуток времени
за промежуток времени 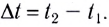
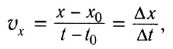
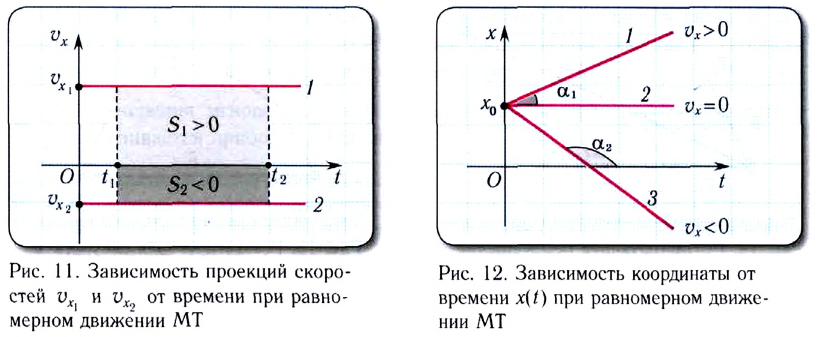
 от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).
от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).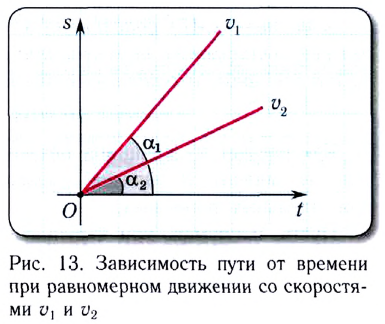
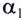 ).
).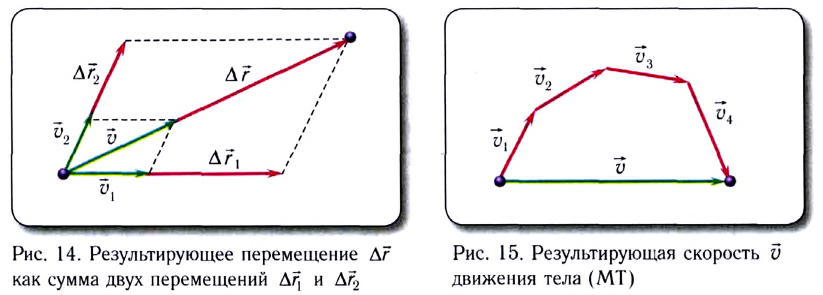

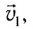 мы движемся на лодке со скоростью
мы движемся на лодке со скоростью 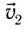 относительно воды. В этом случае результирующее перемещение
относительно воды. В этом случае результирующее перемещение 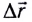 (рис. 14) лодки относительно берега будет складываться из собственного перемещения
(рис. 14) лодки относительно берега будет складываться из собственного перемещения 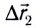 относительно воды и перемещения
относительно воды и перемещения 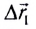 вместе с водой вследствие течения реки:
вместе с водой вследствие течения реки: 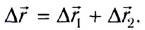
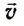 тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей
тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей 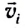 отдельных движений (рис. 15):
отдельных движений (рис. 15):