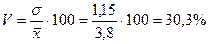Распределение автомобилей автотранспортного предприятия по величине суточного пробега следующие
Контрольная работа по «Статистике»
Автор работы: Пользователь скрыл имя, 14 Апреля 2013 в 13:19, контрольная работа
Описание работы
Потребление электроэнергии в регионе характеризуется следующими данными: 2000 г. – 43,1 млрд. кВт ч; 2001 г. – 49,8 млрд. кВт ч. Численность населения региона составила (млн. чел.): на 01.01.2000 г. – 8,8; 01.01.2001 г. – 9,0; 01.01.2002 г. – 9,3.
Определить, на сколько процентов изменилось потребление электроэнергии на душу населения.
Файлы: 1 файл
статистика.docx
Потребление электроэнергии в регионе характеризуется следующими данными: 2000 г. – 43,1 млрд. кВт ч; 2001 г. – 49,8 млрд. кВт ч. Численность населения региона составила (млн. чел.): на 01.01.2000 г. – 8,8; 01.01.2001 г. – 9,0; 01.01.2002 г. – 9,3.
Определить, на сколько процентов изменилось потребление электроэнергии на душу населения.
Потребление электроэнергии (млрд.кВт ч.)
Численность населения (млн.чел.)
Потребление электроэнергии на душу населения
ТП=(5442,62 кВт ч – 4842,79 кВт ч)/ 4842,70 кВт ч *100%= 12,39%
Вывод: на 12,39% изменилось (увеличилось) потребление электроэнергии на душу населения в 2001 году по сравнению с 2000 г.
Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее ( табл. 10)
Суточный пробег автомобиля, км.
Определить средний суточный пробег одного автомобиля.
Суточный пробег автомобиля, км.
Вывод: Средний суточный пробег одного автомобиля составляет 183,1 км.
Средняя величина признака равна 2600 единицам, а коэффициент вариации равен 30%. Определить дисперсию признака.
Вывод: Дисперсия признака равна 608400.
Количество произведенной продукции в натуральном выражении уменьшилось на 2,5%, а отпускные цены на продукцию увеличились на 5,2%. Определить, на сколько процентов изменилась стоимость продукции в отчетном году по сравнению с прошлым годом.
Вывод: Стоимость продукции в отчетном году по сравнению с прошлым годом увеличилась на 2,6%.
ПН=320-13,2+17,5= 324,3 (тыс.чел.)
Вывод: Численность постоянного населения города на начало года равна 324,3 тыс.чел.
Имеются данные по области за год (тыс. чел.):
1. Трудоспособное население в трудоспособном возрасте 792,6
2. Работающие лица пенсионного возраста и подростки 19,2
3. Численность занятых:
а) в сфере производства продуктов 316,3
б) в сфере производства услуг 330,1
в) учебой с отрывом от производства, домашним
хозяйством и уходом за детьми 165,4
1. Численность трудовых ресурсов по источникам формирования.
2. Численность трудовых ресурсов по фактической их занятости.
Вывод: Численность трудовых ресурсов по источникам формирования составляет 1604,4 тыс.чел.;
численность трудовых ресурсов по фактической их занятости составляет 1458,2 тыс.чел.
Имеются следующие данные по экономике за год в текущих ценах, млрд. руб.:
1. Выпуск товаров и услуг в основных ценах 4393,4
2. Промежуточное потребление 2086,7
3. Косвенно измеряемые услуги финансового
4. Налоги на продукты 320,3
5. Субсидии на продукты 104,9
Определите валовой внутренний продукт в рыночных ценах производственным методом.
ВВП= 4393,4-2086,7-7,4+320,3-104,9= 2514,7 (млрд.руб.)
Вывод: Валовой внутренний продукт в рыночных ценах производственным методом составляет 2514,7 млрд.руб.
Расчет показателей вариации
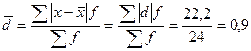
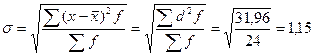
Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1,15 разряда, или на 30,3%.
Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних.
Значение коэффициента вариации (30,3%) свидетельствует о том, что совокупность достаточно однородна.
Как видно на рис. 3.1, распределение рабочих по тарифному разряду несимметрично, поэтому определяется показатель асимметрии:

Следовательно, асимметрия левосторонняя, незначительная.
2. Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая следующее (табл 5).
| Суточный пробег (км), х | 100-125 | 125-150 | 150-200 | Итого |
| Число автомобилей, f |
Требуется построить вариационный ряд с равными интервалами в 20 км.
Построение нового ряда с равными интервалами осуществляется в следующей последовательности.
1. Записывается макет таблицы нового ряда (табл. 6).
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
2. Определяется абсолютная плотность имеющегося распределения с неравными интервалами:
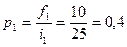
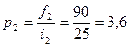
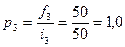
3. Находятся частоты для каждой группы нового ряда по формуле:
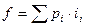
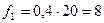
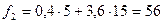
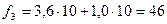
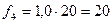
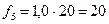
4. Оформляется новый ряд распределения с равными интервалами.
Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая представлено в табл. 7.
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
3. Дневная производительность труда рабочих бригады, выполняющих одинаковую операцию по обработке детали № 408, следующая (табл. 8).
| Дневная производительность труда (шт.), х | Итого |
| Число рабочих, f |
Определить численное значение медианы.
Совокупность содержит четное число значений признака, по
этому медиана определяется по формуле:
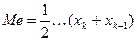
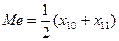
Для определения численных значений х10 и х11 исчисляются накопленные частоты (табл. 9).
| Дневная производительность труда (шт.), х |
| Число рабочих, f |
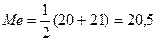
4.Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250.
Найти среднюю величину.
Для нахождения средней величины воспользуемся формулой
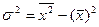
где 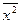
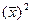
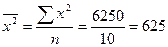
Средняя величина признака
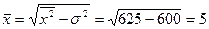
Методические указания для студентов по проведению практических занятий по дисциплине «Статистика» (стр. 17 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
Гистограмма строится в прямоугольной системе координат. По оси абсцисс откладывают интервалы значений вариационного признака, причем число интервалов целесообразно увеличить на два (по одному в начале и в конце имеющегося ряда) для удобства преобразования гистограммы в полигон частот. На отрезках (интервалах) строятся прямоугольники, высота которых соответствует частоте.
Для преобразования гистограммы в полигон частот середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов, в которых частоты равны нулю.
На рисунке 3.2 представлено графическое изображение построенного интервального вариационного ряда в виде гистограммы и полигона частот.
Как видно из графика, треугольники, относящиеся к площади гистограммы и к площади полигона, попарно равны между собой, и, следовательно, площадь гистограммы и площадь полигона данного вариационного ряда также совпадают.
На основе построенной гистограммы графически можно определить значение моды. Для этого правую вершину модального прямоугольника соединяют прямой с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяют с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. Мо = 28,3 года. На рис. 3.2 эти прямые линии, соединяющие вершины прямоугольников, и перпендикуляр из точки их пересечения показаны пунктирной линией.
На рисунке 3.3 представлена кумулятивная кривая (кумулята).
Кумулята может быть использована для графического определения медианы. Для этого последнюю ординату кумуляты делят пополам. Через полученную точку проводят прямую, параллельную оси х, до пересечения ее с кумулятой. Из точки пересечения опускается перпендикуляр до оси абсцисс. Абсцисса точки пересечения является медианой. Линии, определяющие медиану, на рис. 3.3 показаны пунктирными линиями. Ме = 28,6 года.
3 Расчет показателей центра распределения:
где х’ — среднее значение признака в интервале (центр интервала).
Для интервального вариационного ряда порядок расчета структурных средних следующий: сначала находят интервал, содержащий моду или медиану, а затем рассчитывают соответствующие значения названных показателей.
Модальным в данном распределении является интервал 27 — 30 лет, так как наибольшее число рабочих ( 
Значение моды, полученное по формуле, соответствует значению, полученному на графике.
Место медианы –
Медианным является также интервал 27 — 30 лет, так как в этом интервале находятся номера 15 и 16 ряда.
Для расчета показателей вариации составляется вспомогательная таблица:
Вспомогательная таблица для расчета показателей вариации
(лет), (
Контрольная работа по «Статистике»
Автор работы: Пользователь скрыл имя, 18 Ноября 2013 в 19:01, контрольная работа
Описание работы
Задание 1 Имеются следующие данные по 20 малым предприятиям.
С целью изучения зависимости между оборачиваемостью оборотных средств и полученной прибылью на малых предприятиях произвести группировку предприятий по оборачиваемости оборотных средств образовав, пять групп с равными интервалами. По каждой группе и всей совокупности подсчитайте: 1. число заводов; 2. среднюю оборачиваемость оборотных средств; 3. размер прибыли – всего и в среднем на одно предприятие. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Содержание работы
Файлы: 1 файл
статистика1.docx
Муниципальное образовательное учреждение
Высшего профессионального образования
По дисциплине «Статистика»
Имеются следующие данные по 20 малым предприятиям:
Продолжительность оборота в днях
Прибыль предприятия, млн. руб.
С целью изучения зависимости между оборачиваемостью оборотных средств и полученной прибылью на малых предприятиях произвести группировку предприятий по оборачиваемости оборотных средств образовав, пять групп с равными интервалами. По каждой группе и всей совокупности подсчитайте: 1. число заводов; 2. среднюю оборачиваемость оборотных средств; 3. размер прибыли – всего и в среднем на одно предприятие. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Группировку предприятий на пять равных групп произвели по оборачиваемости оборотных средств. В каждую группу попало по 5 предприятий. Для каждой группы была подсчитана средняя оборачиваемость оборотных средств, размер прибыли: всего и в среднем на одно предприятие (см. табл.).
Подсчет средней оборачиваемости оборотных средств и среднего размера прибыли вели по простейшей формуле средней:
Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее:
Суточный пробег автомобиля, км.
Определите средний суточный пробег одного автомобиля.
1. (150*12+170*36+190*28+210*25) /(12+36+28+25)=183 км.
2) размах вариации = 210-150=60 км
Для вычисления других показателей составьте расчетную таблицу.
По предприятию имеются следующие данные за два месяца:
Фонд заработной платы, руб.
Средняя месячная заработная плата, руб.
Фонд заработной платы, руб.
Определите изменение (в %) среднего уровня месячной заработной платы рабочих и служащих, а также средней заработной платы работников предприятия в феврале по сравнению с январем.
Средний уровень заработной платы рабочих в январе месяце составлял 1867 рублей. Изменение заработной платы рабочих равно 94 %.
Средний уровень заработной платы служащих в январе месяце составлял 487 рублей 50 копеек. Изменение заработной платы служащих в феврале месяце по сравнению с январем составило 164 %.
Имеются следующие данные о величине межремонтного пробега автомобилей:
Величина межремонтного пробега, тыс.км.
По приведенным данным определить среднюю величину межремонтного пробега, показатели моды и медианы, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию, коэффициент осцилляции, коэффициент вариации, относительное линейное отклонение. Дать графическое изображение ряда в виде гистограммы и кумуляты.
Величина межремонтного пробега, тыс. км
Число автомобилей (f)
Число автомобилей в % к итогу
Середина интервала (Х)
Средняя величина межремонтного пробега рассчитывается по формуле:
Средняя величина межремонтного пробега автомобилей равна 127,52 тыс. км.
Мода рассчитывается по формуле:
Имеются следующие данные о ежеквартальной выплавке чугуна по заводу в текущем году:
Выплавка чугуна, тыс. т
Определить: 1. абсолютный прирост цепной и базисный; 2. средний абсолютный прирост; 3. средний уровень ряда; 4. темп роста; 5. темп прироста; 6. средние темпы роста и средние темпы прироста; 7. абсолютное значение одного процента прироста. Сделать прогноз для первого квартала следующего года, применив метод аналитического выравнивания по прямой. Сделать выводы.
1. Абсолютную величину прироста уровня механизации относительно предшествующего года.
2. Темпы роста и прироста (цепные и базисные) уровня механизации за указанный период.
3. Абсолютные значения одного процента прироста.
4. Средний за период уровень механизации.
5.Среднегодовой темп роста уровня механизации за период.
6. Построить графическое изображение динамического ряда.
7. Результаты вычислений оформить итоговые статистические таблицы.
Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В нем процесс экономического развития изображается в виде совокупности перерывов непрерывного, позволяющих детально проанализировать особенности развития при помощи характеристик, отражающих изменение параметров экономической системы во времени.
Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени.
Существуют различные виды рядов динамики. Их можно классифицировать по следующим признакам.
1. В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
Примером рядов динамики указанных выше видов являются данные табл. 2.1.
2. В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину за определенные интервалы времени (например, за сутки» месяц, год и т. п.), различают соответственно моментные интервальные ряды динамики.
Примером интервального ряда динамики являются данные, приведенные в табл. 2.1.
Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов.
Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, и поэтому их можно суммировать к не содержащие повторного счета.
Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета, например, число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности и в июне. Что это делает бессмысленным суммирование уровней моментах рядов динамики
Расчет показателей вариации


Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1,15 разряда, или на 30,3%.
Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних.
Значение коэффициента вариации (30,3%) свидетельствует о том, что совокупность достаточно однородна.
Как видно на рис. 3.1, распределение рабочих по тарифному разряду несимметрично, поэтому определяется показатель асимметрии:

Следовательно, асимметрия левосторонняя, незначительная.
2. Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая следующее (табл 5).
| Суточный пробег (км), х | 100-125 | 125-150 | 150-200 | Итого |
| Число автомобилей, f |
Требуется построить вариационный ряд с равными интервалами в 20 км.
Построение нового ряда с равными интервалами осуществляется в следующей последовательности.
1. Записывается макет таблицы нового ряда (табл. 6).
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
2. Определяется абсолютная плотность имеющегося распределения с неравными интервалами:



3. Находятся частоты для каждой группы нового ряда по формуле:






4. Оформляется новый ряд распределения с равными интервалами.
Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая представлено в табл. 7.
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
3. Дневная производительность труда рабочих бригады, выполняющих одинаковую операцию по обработке детали № 408, следующая (табл. 8).
| Дневная производительность труда (шт.), х | Итого |
| Число рабочих, f |
Определить численное значение медианы.
Совокупность содержит четное число значений признака, по
этому медиана определяется по формуле:


Для определения численных значений х10 и х11 исчисляются накопленные частоты (табл. 9).
| Дневная производительность труда (шт.), х |
| Число рабочих, f |

4.Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250.
Найти среднюю величину.
Для нахождения средней величины воспользуемся формулой

где 


Средняя величина признака