Машина тьюринга практическая работа

Практическая работа № 36
«Машина Тьюринга»

Файлы-заготовки для выполнения этой практической работы

1. Наберите программу из учебника (или из презентации), которая увеличивает двоичное число на 1 и проверьте её работу.

Будет ли правильно работать эта программа, если вначале каретка расположена справа от числа? Почему?

2. Измените программу для увеличения двоичного числа на 1 так, чтобы она работала правильно, если вначале каретка расположена справа от числа.

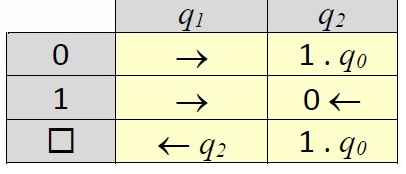
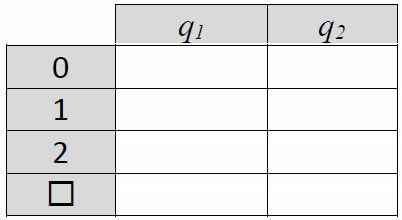
3. Опишите алгоритм работы программы для машины Тьюринга:

При каком начальном состоянии ленты и положении каретки эта программа зацикливается?

4. Составьте программу для машины Тьюринга, которая заменяет в двоичном числе все 0 на 1 и все 1 на 0 (из числа 10101100 получается 01010011). Каретка находится слева от числа.

5. Составьте программу для машины Тьюринга, которая умножает двоичное число на 2. Каретка находится над числом.

6. Составьте программу для машины Тьюринга, которая увеличивает троичное число на 1. Каретка находится справа от числа.

При каком начальном положении каретки эта программа зацикливается?

7. Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1. Каретка находится над числом.

При каком начальном положении каретки эта программа зацикливается?

8. Составьте программу для машины Тьюринга, которая умножает троичное число на 2. Каретка находится над числом.

9. Дана строка, состоящая только из символов «а» и «б». Составьте программу для машины Тьюринга, которая переставляет последний символ в начало строки. Каретка находится над первым символом строки.

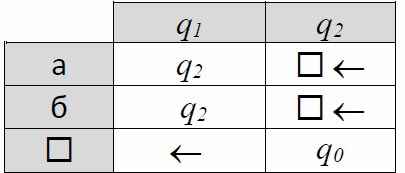
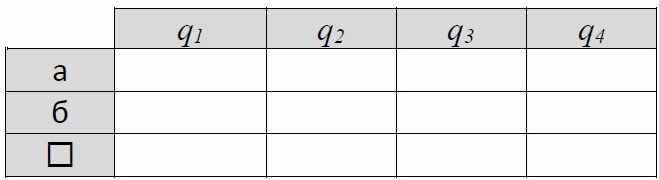
10. *Дана строка, состоящая только из символов «а» и «б». Составьте программу для машины Тьюринга, которая сортирует символы, то есть переставляет все буквы «а» в начало строки. Каретка находится над первым символом строки. Используйте состояния, которые перечислены род таблицей.

11. *Составьте программу для машины Тьюринга, которая складывает два числа в двоичной системе, разделенные на ленте знаком «+».

12. *Составьте программы для машины Тьюринга, которые увеличивают и уменьшают на единицу число, записанное в десятичной системе счисления.

13. Составьте программы для машины Тьюринга, которые выполняют сложение и вычитание двух чисел в десятичной системе счисления.

Источник

Машина тьюринга практическая работа

Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.

Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.

Рассмотрим работу Машины Тьюринга.

Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.

Таким образом Машина Тьюринга формально описывается набором двух алфавитов:

A= — внешний алфавит, служит для записи исходных данных

Q= — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.

Каждая ячейка ленты может содержать символ из внешнего алфавита A = (В нашем случае A=<0, 1>)

Допустимые действия Машины Тьюринга таковы:

1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)

2) сместиться в соседнюю ячейку

3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q

Машина Тьюринга — это автомат, который управляется таблицей.

Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = . В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.

В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «

Источник

Методические рекомендации по выполнению практикума по учебной дисциплине «Теория алгоритмов» (Машина Тьюринга)

Министерство образования и науки Самарской области

Министерство имущественных отношений Самарской области

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Чапаевский губернский колледж»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ СТУДЕНТАМ ПО ВЫПОЛНЕНИЮ ПРАКТИКУМА ПО УЧЕБНОЙ ДИСЦИПЛИНЕ « Теория алгоритмов »

(Раздел 2. Конечные автоматы

Тема 2.2. Рекурсивные функции и понятие вычислимости)

специальность230115 Программирование в компьютерных системах

Публикуется на основании решения

Автор: Дикова В.Г., преподаватель общепрофессиональных и специальных дисциплин ГБОУ СПО «Чапаевский губернский колледж»

Редактор: Следкова М.П., заместитель директора по учебно-методической работе образовательной программы среднего профессионального образования ГБОУ СПО «Чапаевский губернский колледж»

Рецензент: Орлова Н.Н.,

Методические рекомендации предназначены для студентов специальности 230115 Программирование в КС при изучении вычислимости функций и машины Тьюринга как универсального конечного автомата по учебной дисциплине «Теория алгоритмов». Тематика практических заданий соответствует программе учебной дисциплины. Практикум предназначен для закрепления теоретического материала, формирования практических умений студентов в ходе реализации алгоритмов на машине Тьюринга.

Примеры решения задач

Задания для самостоятельной работы

Список источников и литературы

Методические рекомендации по выполнению практикума разработаны в помощь студентам специальности 230115 Программирование в КС для изучения раздела «Конечные автоматы» по дисциплине «Теория алгоритмов».

Тематика практических заданий соответствует программе учебной дисциплины. Практикум предназначен для закрепления теоретического материала, формирования практических умений реализации алгоритмов по заданным параметрам на машине Тьюринга.

При разработке практических заданий учитывались требования к результатам освоения учебной дисциплины, сформулированные в ФГОС СПО III поколения.

В результате освоения раздела обучающийся должен овладеть общими и профессиональными компетенциями, а также

строить принципиальные схемы конечных автоматов;

использовать систему команд машины Тьюринга для записи алгоритма решения задачи;

предупреждать недопустимые действия, ведущие к аварийной остановке машины.

основные модели алгоритмов;

методы построения алгоритмов;

способы построения конечных автоматов;

основной тезис Тьюринга;

устройство машины Тьюринга;

систему команд машины Тьюринга.

Практикум включает в себя теоретическую часть, набор задач с решениями, задания для самостоятельной работы студентов и контрольные задания.

Методические рекомендации могут быть использованы студентами и преподавателями данной дисциплины при подготовке к учебным занятиям.

Машина Тьюринга отличается от человека-вычислителя, выполняющего данные ему предписания, или от реально существующих вычислительных машин в двух отношениях.

Во-первых, машина Тьюринга не может ошибаться, т. е. она строго, без всяких отклонений выполняет программу, определяющую ее работу.

Во-вторых, машина Тьюринга снабжена потенциально бесконечной памятью. Что значит «потенциально бесконечная память»? Это значит, что хотя в каждый момент ее память хранит лишь конечное количество информации, однако для этого количества информации нет никакой верхней границы. Вообразим такую память машины Тьюринга в виде ленты, разделенной на клеточки — ячейки памяти, — которая может быть продолжена вправо сколько угодно

Машина Тьюринга снабжена (в нашем воображении) управляющей головкой, которая в каждый момент обозревает (воспринимает) лишь одну ячейку памяти и может изменить информацию, находящуюся в ней. Представить это можно следующим образом: если в какой-то момент букву в обозреваемой ячейке нужно заменить другой, то старая буква стирается и в ячейку вписывается новая (так же, как на магнитофонной ленте при новой записи автоматически стирается старая запись). Если эту операцию записать в общем виде «s _i  s _j », т. е. буква s _i заменена буквой s _j, то можно выделить следующие частные случаи:

а) i = j, т. е. буква в обозреваемой ячейке не изменилась;

б) i  j – буква изменилась, при этом:

Машина Тьюринга имеет конечное множество внутренних состояний: Q = < q ₀, q₁, q₂, …, q_m>. В каждый данный момент времени машина Тьюринга находится в одном из своих внутренних состояний. После выполнения очередного такта работы машина может изменить свое внутреннее состояние и воспринимать ячейку в следующий момент уже в новом состоянии. Разумеется, внутреннее состояние может остаться и прежним. Если машина в какой-то момент времени попадет в состояние q₀, то ее работа заканчивается (состояние q ₀ называется пассивным). Из множества Q выделим еще одно состояние — q₁ — начальное состояние. В этом состоянии машина всегда начинает свою работу.

Что умеет воображаемая машина?

За один такт работы она может:

изменить содержимое обозреваемой ячейки памяти, т.е. заменить содержащуюся в ней букву алфавита другой;

совершить сдвиг влево или вправо на одну ячейку или остаться на месте и

изменить свое внутреннее состояние.

И больше машина Тьюринга ничего не умеет делать.

Может показаться, что это очень мало. В действительности, это очень много.

Если машина в какой-то момент воспринимает управляющей головкой ячейку, в которой записана буква s_i, и машина находится в состоянии q_j, команда будет записываться в виде трехбуквенного слова s_hTq_p, где Т  <Л, Н, П>, т. е. обозначает один из сдвигов управляющей головки.

Для выполнения команды машина проделывает следующую работу:

буква s_i, находящаяся в обозреваемой ячейке, меняется на s_h;

управляющая головка совершает сдвиг Т, т. е. Л, Н или П;

машина переходит в состояние q_p.

Работа машины состоит из тактов, выполняемых в строгом соответствии с программой. Если в какой-то момент времени машина приходит в состояние q₀, то работа машины заканчивается. Программа полностью определяет работу машины, поэтому можно сказать, что машина Тьюринга задана, если задана ее программа.

Примеры решения задач

1. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q₁ обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

В состоянии q₁ машина ищет правый конец числа, в состоянии q₂ — пропускает знак “+”, при достижении конца последовательности — останавливается. В состоянии q₃ машина знак “+” заменяет на знак “–”, при достижении конца последовательности она останавливается.

2. Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1. Автомат в состоянии q₁ обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Решение этой задачи аналогично рассмотренному выше примеру.

3. Дана десятичная запись натурального числа n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии q₁ обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Состояние q1 — уменьшаем младшую (очередную) цифру на 1. Если она не равна нулю, то после уменьшения сразу — останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. В клетку [a0, q1] машина Тьюринга никогда не попадет, поэтому ее можно не заполнять.

4. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q₁ обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Состояние q1 — уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения — сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q2.

Состояние q2 — после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a0).

Состояние q3 — если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова.

Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.

5. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “( )”.

Автомат в состоянии q₁ обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Состояние q1: если встретили “(”, то сдвиг вправо и переход в состояние q2; если встретили “a0”, то останов.

Состояние q2: анализ символа “(” на парность, в случае парности должны увидеть “)”. Если парная, то возврат влево и переход в состояние q3. Состояние q3: стираем сначала “(”, затем “)” и переходим в q1.

6. Дана строка из букв “a” и “b”. Разработать машину Тьюринга, которая переместит все буквы “a” в левую, а буквы “b” — в правую части строки. Автомат в состоянии q1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

aaa —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

a —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

bbb —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

b —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

ab —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

Машина Тьюринга должна “понимать”, по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние q1 — движение по цепочке из букв “a”, а q2 — состояние движения по цепочке из букв “b”. Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии q1 или q2, т.е. встретили a0, машина должна остановиться, мы обработали всю строку.

Рассмотрим следующие варианты входных слов:

Первый вариант входного слова можно последовательно обработать следующим образом: bba —> bbb —> вернуться к левому концу цепочки из букв “b” —> abb (заменить первую букву в этой цепочке на “a”). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние q2.

7. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2. Автомат в состоянии q₁ обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

состояние q1 — поиск правой (младшей) цифры числа;

состояние q2 — умножение очередной цифры числа на 2 без прибавления 1 переноса;

состояние q3 — умножение очередной цифры числа на 2 с прибавлением 1 переноса.

8. Даны два натуральных числа m и n, представленные в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q₁обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Машина Тьюринга для этой программы выглядит тривиально просто — в ней всего одно состояние. Такая машина Тьюринга выполняет следующие действия: стирает самый правый штрих, ищет разделитель (пустую ячейку) и в эту пустую ячейку помещает штрих, тем самым сформирована непрерывная последовательность штрихов длины n + m.

состояние q1 — поиск разделителя;

состояние q2 — передвинули штрих;

состояние q3 — проверка на конец (все ли штрихи передвинули).

9. Даны два натуральных числа m и n, представленных в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q₁ обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n. Известно, что m > n. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Штрихи начинаем стирать с левого конца массива m. И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n. Но прежде чем стереть правый штрих в массиве n, проверяем, единственный он (т.е. последний, который надо стереть) или нет.

Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.

Состояние q1 — поиск разделителя между массивами штрихов при движении справа налево;

состояние q2 — поиск левого штриха в массиве m;

состояние q3 — удаление левого штриха в массиве m;

состояние q4 — поиск разделителя при движении слева направо;

состояние q5 — поиск правого штриха в массиве n;

состояние q6 — проверка единственности этого штриха в массиве n, т.е. определяем, был ли он последним;

состояние q7 — если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.

10. На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово “да”, иначе — “нет”. Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

При решении этой задачи следует обратить внимание на правильное выписывание алфавита:

Состояние q1 — поиск правого конца числа;

состояние q2 — анализ младшей цифры числа; если она равна “0” или “5”, т.е. число делится на 5, то переход в состояние q3, иначе переход в состояние q5;

состояние q3 — запись буквы “Д” справа от слова на ленте;

состояние q4 — запись буквы “А” справа от слова и останов машины;

состояние q5 — запись буквы “Н” справа от слова;

состояние q6 — запись буквы “Е” справа от слова;

состояние q7 — запись буквы “Т” справа от слова и останов машины.

11. Рассмотрим машину Тьюринга, программа которой задана таблицей:

Алфавит этой машины Тьюринга A = 0, 0, 1,2, 3, 4, 5, 6, 7, 8, 9>, а множество состояний: Q = 0, q₁>

Какую задачу решает эта машина?

Допустим, что в памяти машины перед началом работы хранится число 385, т. е. лента имеет вид, показанный на рисунке:

Из рисунка видно, что машина в состоянии q₁ обозревает самый правый символ записи на ленте. Из программы следует, что соответствующая паре (5,q₁) команда имеет вид: 6Н q ₀. Согласно этой команде машина стирает цифру 5 в обозреваемой ячейке и помещает в ней цифру 6, остается на месте и переходит в состояние q ₀, т. е. останавливается. Таким образом, машина прибавила 1 к исходному числу.

12. Какую работу выполнит машина Тьюринга, если она работает по программе:

Пусть перед началом работы машины ее память (лента) имеет вид

Согласно программе, обозревая ячейку, в которой хранится знак |, и находясь в состоянии q ₁ машина производит следующее действие: не производя никаких изменений в воспринимаемой ячейке, управляющая головка движется вправо и машина остается в состоянии q ₁

Состояние ленты после первого такта работы машины будет таким:

Таким образом, рассматриваемая машина отыскивает первую пустую ячейку справа от воспринимаемой, печатает на ней букву алфавита и останавливается, воспринимая эту ячейку.

Задания для самостоятельной работы

Изобразите на ленте в алфавите 0, |> набор чисел 2, 3, 4, и пусть машина В воспринимает второе число в стандартном положении. Изобразите ленту после работы машины. Какой набор чисел будет записан на ней?

Изобразите на ленте в алфавите < s ₀, |> набор чисел 1, 2, 3 и имитируйте работу машины C (изобразите ленту после каждого такта машины до ее остановки).

Изобразите на ленте числа 3 и 2 в алфавите < s ₀, |>, отделенные друг от друга четырьмя пустыми ячейками. Имитируйте работу машины D применительно к этой записи на ленте.

Машина R, отправляясь от воспринятого в стандартном положении числа, не самого правого на ленте, идет вправо к стандартному положению ближайшего справа числа.

Машина L, отправляясь от воспринятого в стандартном положении числа, не самого левого на ленте, идет влево к стандартному положению ближайшего слева числа.

Список источников и литературы

В.И.Игошин. Математическая логика и теория алгоритмов. [Текст]: В.И. Игошин. – М.: Академия, 2008 г. – 448 с.

Б.Я. Фалевич. Теория алгоритмов. [Текст]: Б.Я. Фалевич. – М.: Машиностроение, 2004 г. – 160 с.

Источник