Определи пример неравномерного движения мотоциклист тормозит у светофора грузовик движется по прямой
Движение автомобиля. Автомобиль набирает скорость постепенно, начиная со стартовой скорости 0 км/ч. В общем в природе не существует ничего равномерного и прямолинейного, это невозможно
Равномерное движение — это движение, при котором тело проходит равные расстояния за небольшие равные промежутки времени.
При равномерном движении скорость тела постоянна. Её легко вычислить: нужно пройденное расстояние поделить на время пути.
Пример равномерного движения. Каждую секунду этот автомобиль проходит путь 50 метров:
Неравномерным называется такое движение, при котором за равные промежутки времени тело проходит различные отрезки пути.
Пример неравномерного движения. Разгоняясь, каждую секунду санки проходят все большие отрезки пути:
Чтобы с уверенностью сказать, что тело двигалось неравномерно, нужно много раз во время движения измерить его положение.
Пример:
1. Группа туристов в походе движется неравномерно — преодолевает примерно одинаковое расстояние днём, а ночью останавливается на стоянку. Если отмечать на карте их положение каждое утро, то флажки будут на одинаковом расстоянии. А если делать отметки ещё и вечером, а лучше — много раз в сутки, то мы увидим, что движение неравномерно.
Примеров равномерного движения в природе очень мало.
2. Почти равномерно движется вокруг Солнца Земля, капают капли дождя, всплывают пузырьки в газировке. Даже пуля, выпущенная из пистолета, движется прямолинейно и равномерно только на первый взгляд. От трения о воздух и притяжения Земли полет ее постепенно становится медленнее, а траектория снижается. Вот в космосе пуля может двигаться действительно прямолинейно и равномерно, пока не столкнется с каким-либо другим телом.
А с неравномерным движением дело обстоит куда как лучше – примеров множество.
3. Полет мяча во время игры в футбол, движения льва, охотящегося на добычу, путешествие бабочки, порхающей над цветком, – все это примеры неравномерного механического движения тел.
Помогите с домашкой по физике
1. определи пример равномерного движения:
грузовик движется по прямой с постоянной скоростью
мотоциклист тормозит у светофора
2.Висящая на дереве груша притягивается к Земле с силой 2,38 Н.
Определи значение силы (в Н), с которой Земля притягивается к груше.
(Из предложенных вариантов ответа выбери наиболее близкий к правильному.)
23,8
2,38
Среди предложенных вариантов ответа нет правильного
0
3.Муха вылетает, держа курс на запад, в безветренную погоду со скоростью 2,8 м/с. Под углом 90 градусов всё время направленно дует ветерок со скоростью 9 м/с. В ответе укажи
модуль скорости, с которой будет сейчас лететь муха относительно стоящих домов.
Ответ округли до десятых.
4.Частота колебаний источника звука равна 7400 Гц. Скорость звука в воздухе составляет 336 м/с.
Определи длину звуковой волны в воздухе (в метрах).
(Выбери и отметь наиболее близкий к правильному ответ среди предложенных.)
2486400
22,024
0
0,045
5. На проводник длиной 0,7 м, расположенный перпендикулярно линиям индукции магнитного поля, действует со стороны поля сила 7 Н. Сила тока в проводнике — 1,4 А. Определи индукцию магнитного поля.
(Ответ округли до десятых.)
Ответ: B=
Тл.
6.
Груз массой 7 кг подвешен к пружине с жёсткостью 19 Н/м. Определи период и частоту колебаний такого маятника. При расчётах прими π=3,14. (Ответы округли до сотых.)
Ответ:
период колебаний равен
с.,
частота колебаний равна
Гц.
7.Конденсатору ёмкостью 9 мкФ сообщили заряд 7 мкКл. Какова энергия заряженного конденсатора?
(Ответ округли до сотых.)
Ответ:
мкДж.
8.Определи электроёмкость конденсатора, если напряжение между его обкладками U= 1 В, а его заряд q=7⋅10−4 Кл. (Ответ округли до десятых.)
Ответ:
мкФ.
9.Уравнение движения тела дано в виде x=4−5t. Вычисли:
1) начальную координату тела: x0=
м;
2) скорость движения: vx=
м/с;
3) проекцию перемещения тела за 2 секунд (-ы): Sx=
м.
10.Цирковой акробат массой 71 кг, бегущий со скоростью 3,7 м/с, догоняет лошадь массой 243 кг, движущуюся со скоростью 2,2 м/с, и вскакивет на неё. Определи скорость лошади в тот момент, когда акробат вскочил на неё.
Ответ (округли до сотых):
м/с.
11.Человек, стоящий на берегу моря, определил, что расстояние между следующими друг за другом гребнями равно 2 м. Также он подсчитал, что за 38 с мимо него прошло 18 волновых гребней.
С точностью до десятых определи скорость распространения волн на море.
Помогите с домашкой по физике
1. определи пример равномерного движения:
грузовик движется по прямой с постоянной скоростью
мотоциклист тормозит у светофора
2.Висящая на дереве груша притягивается к Земле с силой 2,38 Н.
Определи значение силы (в Н), с которой Земля притягивается к груше.
(Из предложенных вариантов ответа выбери наиболее близкий к правильному.)
23,8
2,38
Среди предложенных вариантов ответа нет правильного
0
3.Муха вылетает, держа курс на запад, в безветренную погоду со скоростью 2,8 м/с. Под углом 90 градусов всё время направленно дует ветерок со скоростью 9 м/с. В ответе укажи
модуль скорости, с которой будет сейчас лететь муха относительно стоящих домов.
Ответ округли до десятых.
4.Частота колебаний источника звука равна 7400 Гц. Скорость звука в воздухе составляет 336 м/с.
Определи длину звуковой волны в воздухе (в метрах).
(Выбери и отметь наиболее близкий к правильному ответ среди предложенных.)
2486400
22,024
0
0,045
5. На проводник длиной 0,7 м, расположенный перпендикулярно линиям индукции магнитного поля, действует со стороны поля сила 7 Н. Сила тока в проводнике — 1,4 А. Определи индукцию магнитного поля.
(Ответ округли до десятых.)
Ответ: B=
Тл.
6.
Груз массой 7 кг подвешен к пружине с жёсткостью 19 Н/м. Определи период и частоту колебаний такого маятника. При расчётах прими π=3,14. (Ответы округли до сотых.)
Ответ:
период колебаний равен
с.,
частота колебаний равна
Гц.
7.Конденсатору ёмкостью 9 мкФ сообщили заряд 7 мкКл. Какова энергия заряженного конденсатора?
(Ответ округли до сотых.)
Ответ:
мкДж.
8.Определи электроёмкость конденсатора, если напряжение между его обкладками U= 1 В, а его заряд q=7⋅10−4 Кл. (Ответ округли до десятых.)
Ответ:
мкФ.
9.Уравнение движения тела дано в виде x=4−5t. Вычисли:
1) начальную координату тела: x0=
м;
2) скорость движения: vx=
м/с;
3) проекцию перемещения тела за 2 секунд (-ы): Sx=
м.
10.Цирковой акробат массой 71 кг, бегущий со скоростью 3,7 м/с, догоняет лошадь массой 243 кг, движущуюся со скоростью 2,2 м/с, и вскакивет на неё. Определи скорость лошади в тот момент, когда акробат вскочил на неё.
Ответ (округли до сотых):
м/с.
11.Человек, стоящий на берегу моря, определил, что расстояние между следующими друг за другом гребнями равно 2 м. Также он подсчитал, что за 38 с мимо него прошло 18 волновых гребней.
С точностью до десятых определи скорость распространения волн на море.
Register
Do you already have an account? Login
Login
Don’t you have an account yet? Register
Newsletter
Submit to our newsletter to receive exclusive stories delivered to you inbox!
Онтонио Веселко
Помогите с домашкой по физике
1. определи пример равномерного движения:
грузовик движется по прямой с постоянной скоростью
мотоциклист тормозит у светофора
2.Висящая на дереве груша притягивается к Земле с силой 2,38 Н.
Определи значение силы (в Н), с которой Земля притягивается к груше.
(Из предложенных вариантов ответа выбери наиболее близкий к правильному.)
23,8
2,38
Среди предложенных вариантов ответа нет правильного
0
3.Муха вылетает, держа курс на запад, в безветренную погоду со скоростью 2,8 м/с. Под углом 90 градусов всё время направленно дует ветерок со скоростью 9 м/с. В ответе укажи
модуль скорости, с которой будет сейчас лететь муха относительно стоящих домов.
Ответ округли до десятых.
4.Частота колебаний источника звука равна 7400 Гц. Скорость звука в воздухе составляет 336 м/с.
Определи длину звуковой волны в воздухе (в метрах).
(Выбери и отметь наиболее близкий к правильному ответ среди предложенных.)
2486400
22,024
0
0,045
5. На проводник длиной 0,7 м, расположенный перпендикулярно линиям индукции магнитного поля, действует со стороны поля сила 7 Н. Сила тока в проводнике — 1,4 А. Определи индукцию магнитного поля.
(Ответ округли до десятых.)
Ответ: B=
Тл.
6.
Груз массой 7 кг подвешен к пружине с жёсткостью 19 Н/м. Определи период и частоту колебаний такого маятника. При расчётах прими π=3,14. (Ответы округли до сотых.)
Ответ:
период колебаний равен
с.,
частота колебаний равна
Гц.
7.Конденсатору ёмкостью 9 мкФ сообщили заряд 7 мкКл. Какова энергия заряженного конденсатора?
(Ответ округли до сотых.)
Ответ:
мкДж.
8.Определи электроёмкость конденсатора, если напряжение между его обкладками U= 1 В, а его заряд q=7⋅10−4 Кл. (Ответ округли до десятых.)
Ответ:
мкФ.
9.Уравнение движения тела дано в виде x=4−5t. Вычисли:
1) начальную координату тела: x0=
м;
2) скорость движения: vx=
м/с;
3) проекцию перемещения тела за 2 секунд (-ы): Sx=
м.
10.Цирковой акробат массой 71 кг, бегущий со скоростью 3,7 м/с, догоняет лошадь массой 243 кг, движущуюся со скоростью 2,2 м/с, и вскакивет на неё. Определи скорость лошади в тот момент, когда акробат вскочил на неё.
Ответ (округли до сотых):
м/с.
11.Человек, стоящий на берегу моря, определил, что расстояние между следующими друг за другом гребнями равно 2 м. Также он подсчитал, что за 38 с мимо него прошло 18 волновых гребней.
С точностью до десятых определи скорость распространения волн на море.
Задачи «разгон» и «торможение»
При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a
Задача «Разгон»
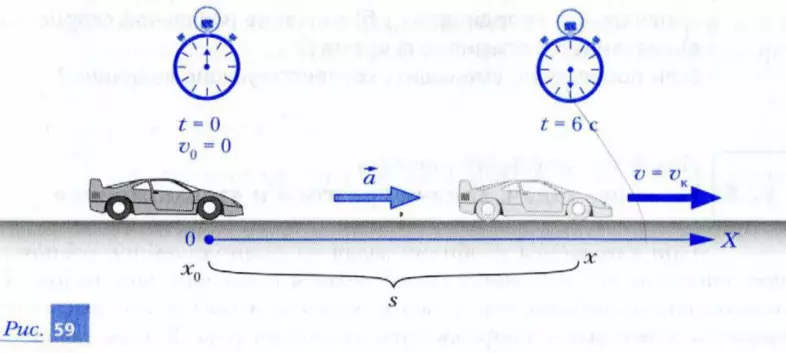
Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.
Решение.
Используем известную нам схему решения кинематических задач.
Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x0 = 0.
Шаг 3. По условию начальная скорость автомобиля v0 = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.
Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:
x = x0 + v0 · t + (a · t 2 ) / 2 = 0 + 0 + (a · t 2 ) / 2 = (a · t 2 ) / 2.
Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:
v = v0 + a · t = 0 + a · t = a · t.
Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).
Шаг 5. Условие окончания разгона до скорости vк имеет вид:
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = (a · t 2 ) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = vк. (3) (условие окончания разгона)
Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:
Подставив полученное значение a в уравнение (1), находим:
x = (a · t 2 ) / 2 = (5 · 6 2 ) / 2 = 90 (м).
Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.
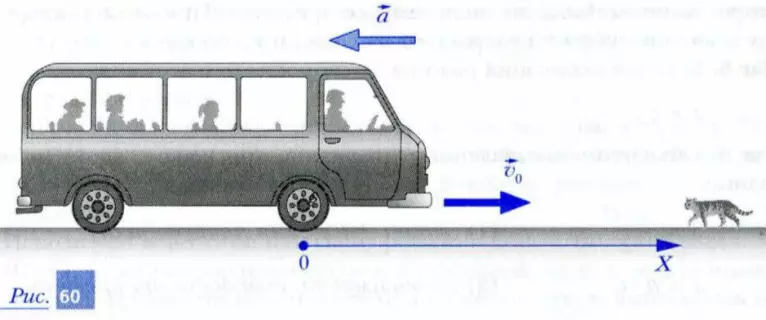
Задача «Торможение»
Решение.
Шаг 1. Систему отсчета выберем так, как показано на рис. 60.
Шаг 2. Начальная координата автобуса x0 = 0.
Шаг 3. Значение начальной скорости автобуса v0 = 20 м/с.
Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:
Шаг 4* (новый). Зависимость значения скорости от времени имеет вид:
Шаг 5. Запишем условие окончания торможения: v = 0, так как в искомый момент времени t автобус должен остановиться.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
Шаг 7. Решение уравнений. Чтобы найти тормозной путь, необходимо подставить в уравнение (1) время торможения автобуса. Эта величина нам неизвестна, но ее можно найти из уравнений (2) и (3). Для этого необходимо подставить в зависимость скорости от времени значение скорости в момент окончания торможения v = 0, после чего решить полученное уравнение:
Таким образом, автобус остановится через время t = 5 с.
Подставим найденное время торможения t = 5 с в уравнение (1) и найдем тормозной путь:
Таким образом, длина тормозного пути автобуса равна 50 м.
Итоги
Если положительное направление оси X выбрать совпадающим с направлением движения тела, то все задачи на равноускоренное движение можно свести к двум типам:
1) задача «разгон» (a > 0, скорость тела увеличивается с течением времени);
2) задача «торможение» (a Если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы, в течение каждого из которых тело движется только в одном направлении. При этом задача разделяется на несколько задач.
Упражнения
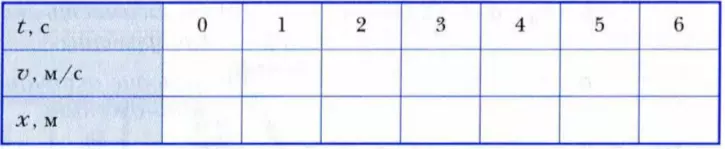
1. Заполните таблицу для разгоняющегося автомобиля, используя условия задачи 1 («разгон»). Как изменяются со временем: значение скорости; координата разгоняющегося автомобиля?
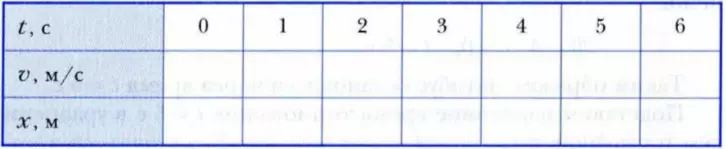
2. Заполните таблицу для тормозящего автобуса, используя условия задачи 2 («торможение»). Ответьте на вопросы: как изменяются со временем: значение скорости; координата тормозящего автобуса?
4. Решите задачу 2 («торможение») в общем виде. Представьте полученный ответ в виде
s = v0 2 / (2 · a).
Проведите анализ полученного ответа. Определите тормозной путь автобуса, если: а) v0 = 16 м/с; б) v0 = 115,2 км/ч.
5. Найдите путь, пройденный автомобилем, движение которого задано в упражнении 3, за промежуток времени от t1 = 2 с до t2 =5 с.
6. Два мотоциклиста, двигавшиеся прямолинейно, начинают одновременно тормозить перед светофором и так же одновременно останавливаются, проехав расстояние s = 100 м. Первый мотоциклист перед торможением двигался со скоростью, имеющей значение v1 = 72 км/ч, второй – со скоростью, имеющей значение v2 = 108 км/ч. Найдите значения ускорений мотоциклистов.