Расчет загрузки автомобиля в excel
Здесь Вы можете произвести расчёты загрузки автомобилей

Всякий, кто занимался организацией грузоперевозок или переездов задавал себе вопрос: сколько это стоит? Это один из основных вопросов и, пожалуй, самый главный, так как решает целесообразность перемещения грузов на расстояния. Эра открытий прошла, уже не осталось белых пятен на картах, наступила эпоха прагматичной целесообразности.
Вопрос: «Во что это обойдется?» решает все.
Вот здесь и пригодятся наши программы расчетов грузоперевозок и переездов.
Калькуляционные расчеты помогут определить целесообразность перемещения практически любых грузов, подобрать нужный транспорт от бычка и газели до большегрузных фур в соответствии с габаритами и тоннажём груза.
Расчеты стоимости перевозок (переездов) нужны как для крупных фирм, с грузопотоком в десятки тысяч тонн, так и частным предпринимателям и домохозяйкам, заказывающим перевозку мебели или крупногабаритной техники.
Мы представляем калькуляционные программы выбора автотранспорта по объему и тоннажу перевозимого груза, а также программы расчетов стоимости перевозок.
3D расчёт загрузки
Пример программы расчёта загрузки
Вы можете скачать эту программу с нашего сайта ввиде zip-архива, в который входят: инструкция и лицензионное соглашение (формат rtf), а так же файлы программы. Данная программа распространяется бесплатно, с обязательным упоминанием этого сайта и ссылкой на эту страницу. Запрещается продавать эту программу и сдавать в аренду, получать коммерческую выгоду. Программа защищена законом © www.wiraj-perevozki.ru, 2011.
Скачать программу 3D загрузки (2,39 МБ)
После скачивания программы распакуйте ZIP архив в любую папку, затем почитайте инструкцию и лицензионное соглашение.
2D расчёт загрузки
Пример программы расчёта загрузки
Вы можете связаться с нами, и мы ответим по вопросам приобретения данной программы.
Программа защищена законом © www.wiraj-perevozki.ru, 2014.
Универсальный расчёт загрузки автомобилей (в Excel)
Пример таблицы в Excel 
Скачать универсальный расчёт (41 кб, xls файл)
для работы этого файла вам потребуется MS Excel
Как решить транспортную задачу в Excel
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 | |
Задача: минимизировать транспортные расходы по перевозке продукции.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Автоматизация и моделирование бизнес-процессов в Excel
Глава 10. Модель для расчета максимальной загрузки автомобиля (контейнера)
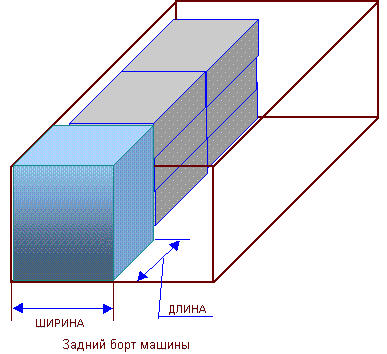
Большинство перевозимых грузов имеет прямоугольную форму — ящики, коробки, упаковки и т.д. При погрузке на транспорт (автомобиль, вагон, контейнер) ящиков в первый раз, предварительно происходит оценка — как оптимально расположить этот груз, чтобы в ограниченный объем вошло максимальное количество ящиков или как вместить в это пространство их необходимое количество. Довольно часто расположение ящиков производится интуитивно. При этом возможны дополнительные потери времени или заполнение ограниченного объема не является самым эффективным. В дальнейшем будем считать, что осуществляется загрузка автомобиля, и габариты ограничены размерами кузова.
Идеальный случай — когда размеры ящиков кратны размерам кузова машины. Тогда посчитать количество вмещаемых ящиков несложно. Второй простой вариант — когда на ящиках указано их возможное расположение, и они размещаются в один ряд.
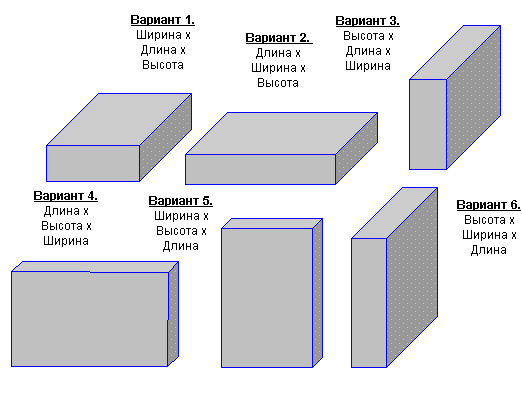
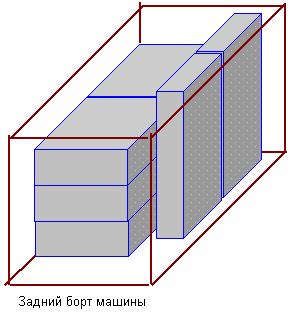
Предположим, что размеры ящиков и кузова машины не кратны, и что эти ящики можно располагать как угодно, то есть на них нет маркировки «верх». В таком случае возможно шесть вариантов расположения груза, которые показаны на рис. 10.1.
Рис. 10.1. Возможное расположение прямоугольных ящиков с грузом в кузове машины
На рис. 10.1. указаны номера вариантов возможного расположения груза в кузове, а также описание варианта расположения ящиков по отношению к переднему борту автомобиля. Например, Вариант 1 — Ширина х Длина х Высота предполагает, что ящик будет расположен шириной по ширине кузова, длиной по длине и высотой по высоте.
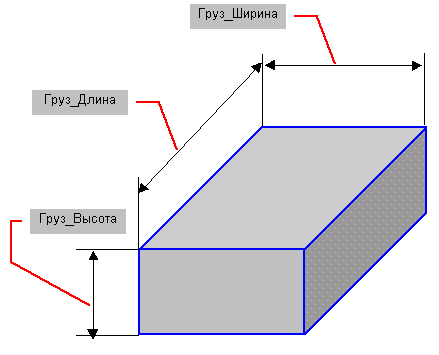
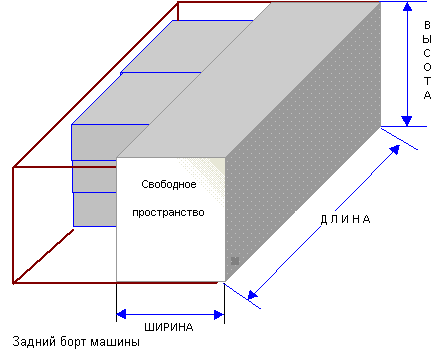
Рис. 10.2. Наименования сторон габаритов груза, применяемые в разрабатываемом приложении в качестве имен ячеек, в которые будет осуществляться ввод этих размеров
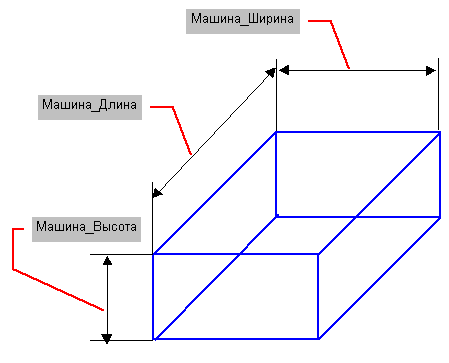
Рис. 10.3. Наименования сторон габаритов кузова автомобиля, применяемые в разрабатываемом приложении в качестве имен ячеек, в которые будет осуществляться ввод этих размеров
Книге, в которой будет производиться расчет оптимальной загрузки транспорта, присвойте имя Груз. Все расчеты будут производиться на одноименном листе Груз.
Исходные данные вводятся в две небольшие таблицы с указанием габаритов кузова машины (диапазон ячеек В1:С4) и габаритов груза (диапазон ячеек В6:С9), а также количество ящиков, которые желательно разместить в этом кузове (ячейка С11). Ячейкам, в которые будут вводиться габариты груза и кузова, присвойте имена, показанные на рис. 10.2. и 10.3.
В качестве единицы измерения будут указаны метры, хотя это и не так и важно. В правой части рабочего листа на рис. 10.4. находится таблица с выходными параметрами, которая будет рассмотрена в конце этой главы. Задача приложения — найти оптимальные варианты загрузки автомобиля, при которых в кузов должно поместиться максимальное количество ящиков.
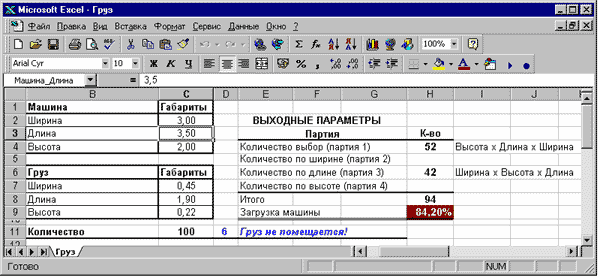
Предполагаемая последовательность заполнения кузова автомобиля
Прежде чем приступить к созданию модели, необходимо продумать последовательность выполнения расчетов, которые в свою очередь предполагают виртуальную последовательность погрузки ящиков в кузов. Немаловажной деталью является и определение позиции наблюдающего за погрузкой, например, с целью- какой угол является правым или левым. Предполагаем, что наблюдение за погрузкой будет осуществляться от заднего борта автомобиля.
Предполагаем, что последовательность заполнения кузова автомобиля ящиками с грузом будет разделена на несколько этапов, каждый из которых предполагает погрузку партии ящиков.
Первый этап — загрузка первой партии (партия-1), которая будет производиться от левого дальнего угла кузова при возможном размещении груза по одному из шести выбранных вариантов. При моделировании возможного размещения ящиков первой партии, должна присутствовать возможность анализа размещения ящиков по всем шести вариантам. При этом исходными данными для расчета будут служить значения габаритов кузова, которые введены в таблицу исходных данных (рис. 10.4.).
На рис. 10.5. в качестве примера показано расположение первой партии груза по варианту 1.
Рис. 10.5. Заполнение кузова автомобиля первой партией (выбрано расположение по варианту 1 — Ширина х Длина х Высота)
Следовательно для последующих расчетов исходными данными будут служить уже значения габаритов оставшихся трех свободных объемов пространства кузова, не занятые ящиками первой партии.
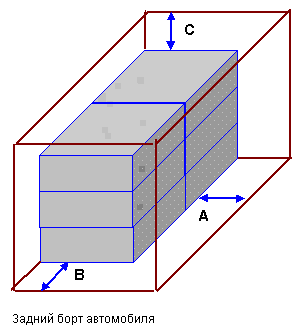
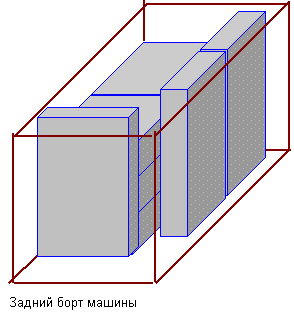
Следующей, второй партией (партия-2), например, осуществляется загрузка свободного пространства кузова от правой линии загруженных ящиков до правого борта кузова по всей длине кузова и на всю высоту кузова (рис. 10.6.). Предполагаемое расположение груза на рисунке выбрано по варианту 6 — Высота х Ширина х Длина.
Рис. 10.6. Заполнение свободного пространства кузова автомобиля второй партией ящиков с грузом по варианту 6 размещения
Третьей партией (партия-3) осуществляется загрузка свободного пространства кузова от линии загруженных ящиков первой партии по ширине кузова до правой линии загруженных ящиков второй партии и на всю высоту кузова (рис. 10.7.). Ящики третьей партии на рисунке загружаются по варианту 5 — Ширина х Высота х Длина.
Рис. 10.7. Заполнение свободного пространства кузова автомобиля третьей партии по варианту 5 размещения
И последняя партия груза (партия-4) будет упаковываться, при наличии свободного пространства, поверх первой партии. Последовательность загрузки при желании может быть изменена, но результат от этого не изменится.
Определение оптимального варианта размещения первой партии груза
В зависимости от выбранного варианта размещения первой партии груза, в кузов автомобиля может поместиться различное количество ящиков этой партии. Создаваемая таблица должна учитывать выбираемый вариант размещения груза, производить расчет помещаемых ящиков по ширине, длине и высоте кузова, а также общее количество ящиков в первой партии и используемый объем кузова автомобиля.
Создание таблицы для расчета объема занимаемого первой партией груза
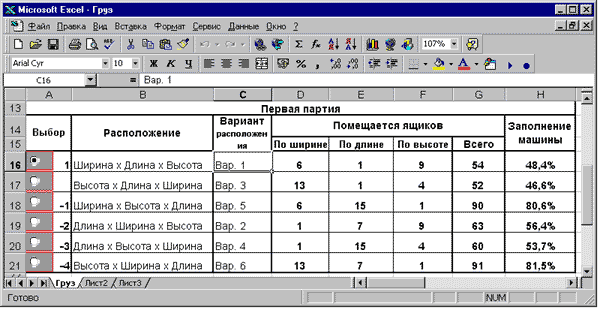
Определение оптимального заполнения кузова машины первой партией груза будет производиться в таблице, расположенной в области А13:Н21 (рис. 10.8.).
Рис. 10.8. Таблица для расчета количества помещаемых ящиков и заполнения пространства кузова при размещении первой партии груза с числовым примером
Автоматизация выбора варианта расположения груза первой партии
Для выбора варианта расположения первой партии груза в кузове автомобиля могут быть использованы шесть элементов управления Переключатель, которые связаны с ячейкой А16. В ячейку А17 введите формулу:
Формулы расчета количества ящиков первой партии
Формулы расчета должны определять количество размещаемых ящиков в один ряд по каждому параметру кузова автомобиля (по ширине, по длине и по высоте).
Например, в диапазоне ячеек D16:D21 необходимо произвести расчет количества ящиков, которые разместятся в один ряд по ширине автомобиля при каждом варианте размещения первой партии ящиков. Для этого необходимо произвести операцию деления значения размера ширины кузова автомобиля, находящегося в ячейке С2 (ячейке присвоено имя Машина_Ширина) на первый параметр габарита груза по варианту, текст которой указан в диапазоне ячеек В16:В21. В ячейке D16 будет находиться формула:
потому что в ячейке В16 введен первый вариант расположения груза с первым параметром расположения груза — ширина. В связи с тем, что дробная часть габаритов ящика груза не может быть размещена, в основе формулы используется функция ОТБР, которая отбрасывает дробную часть, получаемую при делении.
Аналогично производится и расчет количества ящиков, размещаемых по длине и высоте при различных вариантах расположения груза. В диапазоне G16:G21 производится расчет общего количества ящиков в первой партии по каждому варианту размещения, путем умножения количества ящиков, размещаемых в один ряд по ширине, по длине и по высоте.
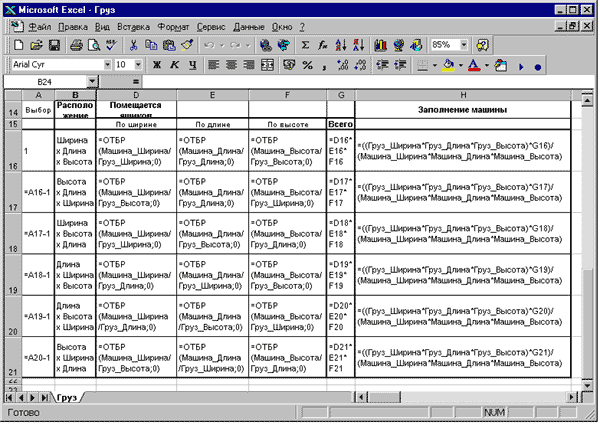
Формулы находящиеся в этой таблице показаны на рис. 10.9.
Рис. 10.9. Таблица для расчета количества помещаемых ящиков и заполнения пространства кузова при размещении первой партии груза с формулами
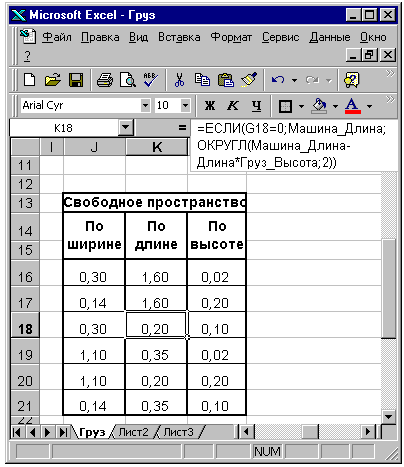
Анализ и расчет свободного пространства кузова после загрузки первой партии ящиков
Создание таблицы расчета размеров оставшегося свободного пространства в кузове автомобиля
Рис. 10.10. Таблица расчета размеров оставшегося свободного пространства кузова после загрузки первой партии
Формулы в этих областях однотипны и проанализируем их по формуле, введенной в ячейку К16, которая производит вычисление свободного расстояния по длине кузова автомобиля:
Функция ЕСЛИ анализирует, помещается ли груз в машину при данном варианте размещения и если не помещается, то возвращает значение длины автомобиля. Если же груз помещается, то из значения длины кузова автомобиля вычитается значение расстояния, которое занимает габарит груза (по варианту размещения — длина, ширина или высота), умноженный на количество ящиков, размещенных по длине кузова.
В других ячейках таблицы находятся похожие формулы, но используют комбинацию различных габаритов груза и кузова.
Определение составляющих оставшегося свободного объема кузова автомобиля
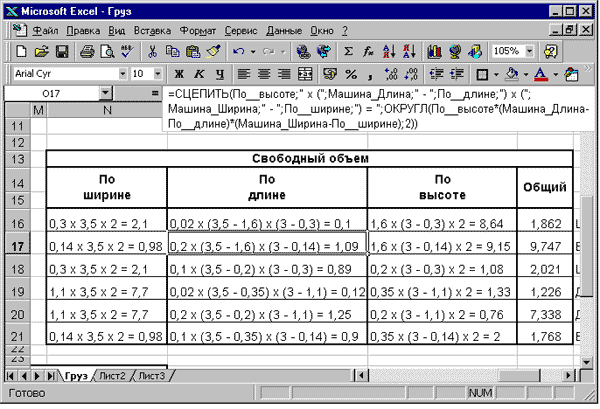
Формулы таблицы расчета оставшегося свободного объема кузова
Рис. 10.11. Таблица расчета оставшегося свободного объема кузова
Рассмотрим формулы, находящиеся в первой строке указанных диапазонов таблицы.
Формула в ячейке N16 основана на функции СЦЕПИТЬ соединяющей текст, ссылки на ячейки, которым присвоены и не присвоены имена, а также производящая вычисление свободного объема, оставшегося по ширине автомобиля:
=СЦЕПИТЬ(J16;» х «;Машина_Длина;» х «;Машина_Высота;» = «;J16*Машина_Длина*Машина_Высота)
Формула в ячейке О16 аналогична предыдущей, но несколько сложнее:
=СЦЕПИТЬ(L16;» х («;Машина_Длина;» — «;K16;») х («;Машина_Ширина;» — «;J16;») = «;ОКРУГЛ(L16*(Машина_Длина-K16)*(Машина_Ширина-J16);2))
И в формуле в ячейке Р16:
=СЦЕПИТЬ(K16;» х («;Машина_Ширина;» — «;J16;») х «;Машина_Высота;» = «;ОКРУГЛ(K16*(Машина_Ширина-J16)*Машина_Высота;2))
В ячейке Q16 формула суммарного свободного объема автомобиля:
Дальнейшее заполнение кузова
После загрузки первой партии ящиков, оставшееся свободное пространство кузова можно разделить на три части (описано выше).
Моделирование возможности дальнейшей автоматизации вычислений
Рассмотрим пример, когда первая партия груза была расположена по варианту 1, для чего активизируйте первый переключатель. Тогда по ширине кузова уместится 6 ящиков, по длине — 1 и по высоте — 9. Всего расположено 54 ящика, и загрузка машины составила 48,4% объема (рис. 10.8.).
Рис. 10.12. Габариты пространства, заполняемого второй партией груза
Тогда длина и высота останутся прежними, а ширина этого свободного объема будет равна ширине кузова автомобиля минус произведение, равное значению ширины груза, умноженное на 6 расположенных ящиков по ширине кузова:
ШИРИНА = 3 — 6 х 0,45 = 3 — 2,7 = 0,3 (м)
Впрочем габариты этого свободного пространства (0,3м х 3,5 м х 2м) и его объем (2,1м3) рассчитаны и показаны в ячейке N16 (рис. 10.11.). Введите значение ширины этого пространства (0,3м) в ячейку С2 области ввода значения габаритов кузова автомобиля (рис. 10.4.) и тогда в таблице, показанной на рис. 10.8., будет произведен расчет, согласно которому возможно максимальное размещение в этом объеме семи ящиков по варианту 6 размещения груза.
Подобный поиск полной оптимальной загрузки автомобиля довольно трудоемок. Поэтому следующая задача — создать еще одну таблицу, которая будет автоматически определять оставшееся свободное пространство по ширине кузова и определять оптимальное последующее расположение второй партии груза при выбранном варианте расположения первой партии груза.
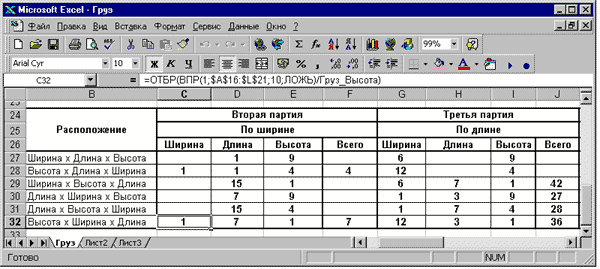
Расчет заполнения свободного объема кузова второй партией груза
Отличие таблицы расчета оптимальной загрузки свободного пространства кузова второй партией груза (рис. 10.13.) заключается только в формулах в столбце С — определение количества располагаемых ящиков по ширине кузова автомобиля, в зависимости от варианта расположения груза. Поэтому эта таблица создается копирование таблицы в области В16:G21 и последующим незначительным редактированием.
Рис. 10.13. Таблица оптимального размещения груза второй и третьей партии ящиков в свободном объеме кузова автомобиля
Находящаяся в ячейке С32 формула (показана в строке формул на рис. 10.13.), в качестве значения размера ширины габаритов свободного пространства, использует рассчитанные данные оставшегося не занятого расстояния ширины кузова автомобиля в области ячеек J16:J21 (рис. 10.10.). Эти данные она находит с помощью функции ВПР по значению 1, которая вводится в область ячеек А16:А21 активизацией выбранного элемента управления Переключатель. Данные свободного пространства, рассчитанные в области ячеек J16:J21 делятся на первый указанный в области ячеек В27:В32 элемент габарита груза (длина, ширина или высота).
Расчет заполнения свободного пространства кузова третьей партии груза
Рис. 10.14. Объем пространства, заполняемого третьей партией груза
Таблица расчета количества ящиков третьей партии находится в области ячеек G27:J33 (рис. 10.13.). Формула в ячейке G27:
производит с помощью функции ВПР поиск размера оставшегося свободного пространства по ширине кузова в области ячеек J16:J21 по выбранному варианту размещения первой партии груза, которое вычитается из ширины кузова автомобиля. И полученный результат делится на габарит груза, который указан первым в вариантах размещения в ячейках В27:В32.
Формула в ячейке Н27:
похожа на предыдущую формулу с той разницей, что поиск оставшегося свободного пространства кузова производится в диапазоне ячеек К16:К21, оставшейся после размещения первой партии груза.
Расчет заполнения свободного объема кузова четвертой партией груза
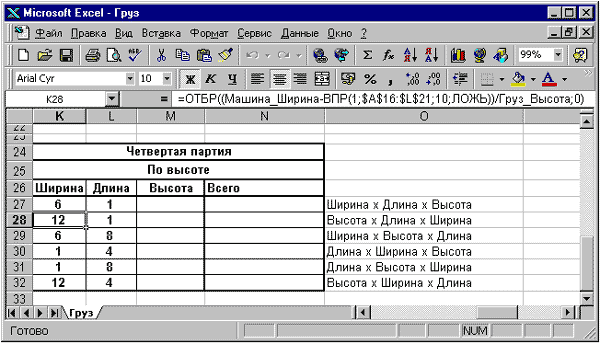
При погрузке четвертой партии ящиков, осуществляется загрузка последнего оставшегося свободного пространства кузова после погрузки трех предыдущих партий. Размеры этого свободного пространства — определяется площадью погруженной первой партии и оставшейся высотой кузова автомобиля. Расчет возможно поместившихся ящиков производится в таблице показанной на рис. 10.15.
Обратите внимание на столбец О — в него дополнительно введены возможные варианты расположения груза. Эти данные, находящиеся справа от области таблицы, пригодятся при формировании итоговой таблицы вывода параметров расчета загрузки всей машины.
Рис. 10.15. Таблица расчета заполнения свободного объема кузова четвертой партии груза
Последовательность загрузки кузова на практике
Может возникнуть вопрос, что свободное пространство для погрузки ящиков четвертой партии будет недоступно после загрузки предыдущих трех партий. Или при полной погрузке первой партии груза, ящики из второй партии будет трудно поместить в правый дальний угол кузова. Но описанная выше последовательность, разделенная на четыре этапа, была необходима только для одного — для поиска последовательности расчетов. На практике, ящики из всех четырех партий, могут размещаться в комбинированном порядке, с позиции доступности места, в котором они должны быть расположены. Ведь уже известно, каким образом (по какому варианту) эти ящики будут располагаться в этом месте.
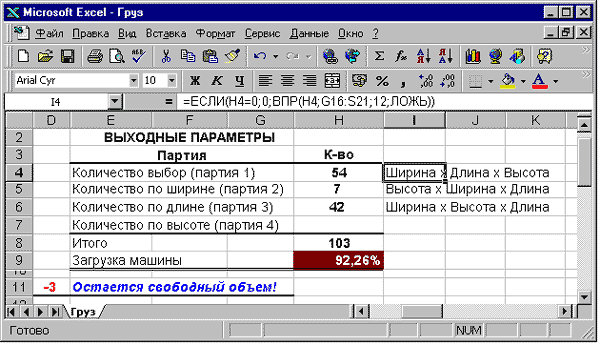
Рис. 10.16. Итоговая таблица с анализом загрузки автомобиля
Расчет общего количества ящиков, которые могут поместиться в кузов автомобиля
При расчете оптимальной загрузки автомобиля необходимо определить — сколько ящиков поместится в машину. Существует и второй аспект этой проблемы — сколько времени потребуется для загрузки самой оптимальной партии.
Таблица с выходными данными предназначена не только для вывода информации по количеству ящиков, которые могут поместиться в кузов автомобиля. Но и может выступать в качестве технологической карты при непосредственной загрузке автомобиля, потому что в ячейках I4:I7 формируется текст вариантов погрузки каждой партии, согласно которого будет известно, как этот груз располагать. А, следовательно, задача сводится к следующему — загрузка автомобиля оптимальной (рассчитанной) партией груза за наиболее короткое время.
Определение оптимального количества ящиков
При активизации переключателей, определяющей вариант размещения ящиков первой партии груза, вычисленные значения таблицы загрузки первой партии товара остаются неизменны. Изменяется только значение количества ящиков груза первой партии, которая отображается в ячейке Н4 таблицы с выходными параметрами, в которой находится формула, производящая поиск количества погруженных ящиков в первой партии рассчитанных в области L16:L21:
Формулы в ячейках Н5:Н7 производят выборку максимального значение, рассчитанное таблицами загрузки второй — четвертой партии груза:
В ячейке Н8 находится формула суммирования количества ящиков во всех четырех партиях.
Формула в ячейке Н9 определяет загрузку объема кузова в процентном отношении:
Если в ячейку С11 введено количество ящиков, предполагаемое для загрузки, то формула в ячейке D11 сравнивает это значение, со значением в ячейке Н8:
В ячейке Е11, в зависимости от полученного результата вычислений в ячейке D11, формируется надписи: Остается свободный объем! или Груз не помещается! по формуле:
Бизнес-события
 |
 |
 |
| МЕТОДОЛОГИЯ: Стратегия, Маркетинг, Изменения, Финансы, Персонал, Качество, ИТ АКТУАЛЬНО: Новости, События, Тенденції, Интервью, Бизнес-образование, Комментарии, Рецензії, Консалтинг СЕРВИСЫ: Бизнес-книги, Работа, Семинары, Форумы, Глоссарий, Цитаты, Рейтинги, Ресурсы, Статьи партнеров ПРОЕКТЫ: Блог, Видео, Визия, Визионеры, Бизнес-проза, Бизнес-юмор |





Copyright © 2001-2021, Management.com.ua
Портал создан и поддерживается Strategic
Подписка на Менеджмент.Дайджест
Получайте самые новые материалы на свой e-mail (1 раз в неделю)