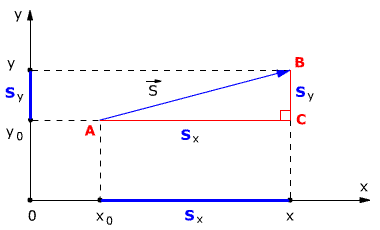
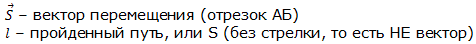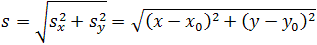На рисунке изображена траектория движения автомобиля определите модуль вектора перемещения
1.1. Кинематика
Примеры заданий ЕГЭ по теме 1.1. «Кинематика»
Часть 1
При выполнении заданий уровня А нужно поставить знак «х» в клеточку, номер которой соответствует номеру выбранного варианта ответа.
А1. На рисунке изображена траектория движения автомобиля. Модуль вектора перемещения из точки А в точку В составляет
1) 6 км 2) 10 км 3) 3,5 км 4) 5 км
А2. На рисунке а приведен график движения тела. Ему соответствует зависимость скорости от времени, представленная на
АЗ. Тело двигалось из точки А в точку В с переменной скоростью, преодолев первый участок пути в 5 м за 8 с, второй участок в 3 м — за 10 с и третий участок длиной 10 м за 18 с. Средняя путевая скорость движения между точками А и В составила
1) 0,5 м/с 2) 2 м/с 3) 0,3 м/с 4) 1 м/с
А4. График зависимости скорости от времени, изображенный на рисунке, описывает:
1) равномерное движение 3) равнозамедленное движение
2) равноускоренное движение 4) отсутствие какого-либо движения
А5. Точка совершает равномерное движение вдоль окружности радиусом В = 5 м со скоростью 3 м/с. Ее центростремительное ускорение при этом равно:
1) 2,5 м/с2 2) 1,8 м/с2 3) 1,5 м/с2 4) 3 м/с2.
А6. Угловая скорость минутной стрелки часов составляет:
1) 0,00174 рад/с 2) 0,005 рад/с 3) 0,003 рад/с 4) 0,04 рад/с.
А7. В безветренную погоду капли дождя падают на землю вертикально. При этом след от капель на окне поезда, движущегося с постоянной скоростью относительно наблюдателя, стоящего на платформе, представляет собой:
1) прямую горизонтальную линию 3) гиперболу
2) прямую вертикальную линию 4) параболу.
Часть 2
Ответом к заданиям В1— В2 будет некоторое число. Это число нужно записать без указания единиц измерения физических величин.
В1. Пользуясь графиком зависимости скорости от времени, изображенным на рисунке, определите путь, пройденный телом за первые 3 минуты.
В2. Мгновенное ускорение тела, движущегося по окружности, равно 5 м/с2, при этом его центростремительное ускорение составляет 4 м/с2. Каково тангенциальное ускорение тела?
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.
На рисунке изображена траектория движения автомобиля определите модуль вектора перемещения
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.
Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.
Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.
ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.
РЕШЕНИЕ:
РЕШЕНИЕ:
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
Траектория
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
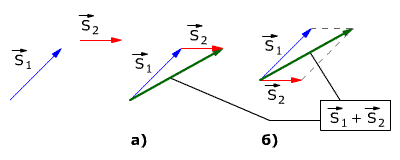
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 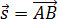
Выберем ось ОХ так, чтобы вектор 
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
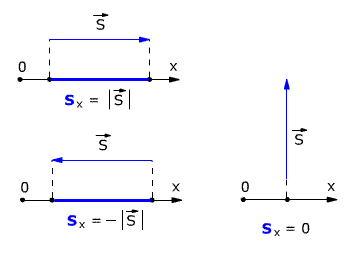
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
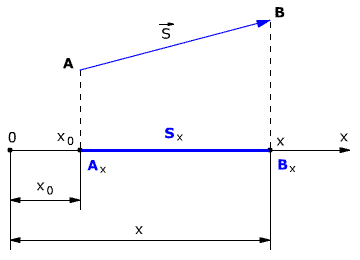
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
По теореме Пифагора
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Тест по физике для подготовки к ЕГЭ
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
1.01. В какой из двух задач можно рассматривать Землю как материальную точку?
1) Рассчитать период обращения Земли вокруг Солнца.
2) Рассчитать скорость движения точек поверхности Земли при ее суточном вращении вокруг своей оси.
А) только в первом случае; Б) только во втором случае; В) в обоих случаях.
1.02. Велосипедист движется из точки А велотрека в точку В по кривой АВ. Назовите
физическую величину, которую изображает вектор АВ.

1.03. Какие из перечисленных величин являются скалярными?
А) скорость; Б) путь; В) перемещение.
1.04. Какая из приведенных формул соответствует определению скорости?
A ) 



1.05. Какая из приведенных формул соответствует определению ускорения?
А) 



1.06. У верхнего конца трубки, из которой выкачан воздух, находятся дробинка, пробка, птичье перо. Какое из этих тел при одновременном старте первым достигает нижнего конца трубки?
А) дробинка; Б) пробка; В) перо; Г) все тела.
1.07. Тело движется равномерно по окружности в направлении против часовой стрелки. Какая стрелка указывает направление вектора скорости тела в точке 1?

1 3 А) 1; Б) 2; В) 3; Г) 4.
1.08. Тело движется равномерно по окружности. Какая стрелка указывает направление вектора ускорения тела в точке М траектории?

1 3 А) 1; Б) 2; В) 3; Г) 4.
1.09. Что измеряет спидометр автомобиля?
А) ускорение; Б) модуль мгновенной скорости;
В) среднюю скорость; Г) перемещение.
1.11. По графику зависимости скорости тела от времени определите пройденный телом путь за 2 с.
v 

1.12. Автомобиль, движущийся прямолинейно равноускоренно, увеличил свою скорость с
3 м/с до 9 м/с за 6 секунд. С каким ускорением двигался автомобиль?
1.13. Автомобиль трогается с места и движется с возрастающей скоростью прямолинейно.
Какое направление имеет вектор ускорения?
А) ускорение равно 0; Б) направлен против движения автомобиля;
В) направлен в сторону движения автомобиля.
1.14. Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет
вектор ускорения?
А) ускорение равно 0; Б) направлен против движения автомобиля;
В) направлен в сторону движения автомобиля.
1.15. Скорость и ускорение движущегося шарика совпадают по направлению. Как
изменяется модуль скорости шарика в этом случае?
А) увеличивается; Б) уменьшается; В) не изменяется.
1.16. Физические величины бывают векторными и скалярными. Какая физическая величина из перечисленных является скалярной?
А) ускорение; Б) время; В) скорость; Г) перемещение.
1.17. Какая единица времени является основной в Международной системе единиц?
А) 1с; Б) 1 мин.; В) 1 час; Г) 1 сутки.
1.18. Основными единицами длины в СИ являются:
А) километр; Б) метр; В) сантиметр; Г) миллиметр.
1.19. Какие из перечисленных ниже величин являются векторными:
1) путь, 2) перемещение, 3) скорость?
А) 1 и 2; Б) 2; В) 2 и 3; Г) 3 и 1.
1.20. В каких случаях космические корабли можно рассматривать как материальные точки?
1) Рассчитать маневр стыковки двух космических кораблей;
2) Рассчитать период обращения космических кораблей вокруг Земли.
А) в первом; Б) во втором; В) в обоих случаях; Г) ни в каком.
1.21. Два автомобиля движутся по прямому шоссе в одном направлении. Если направить ось ОХ вдоль направления движения тел по шоссе, тогда какими будут проекции скоростей автомобилей на ось ОХ?
А) обе положительные; Б) обе отрицательные;
А) равномерными; Б) неравномерными;
В) первого неравномерным, второго равномерным;
Г) первого равномерным, второго неравномерным.
1.23. По графику зависимости пройденного пути от времени при равномерном движении определите скорость велосипедиста в момент времени t = 2 с.
4 А) 2 м/с; Б) 3 м/с; В) 6 м/с; Г) 18 м/с.
1.24. На рисунке представлены графики зависимости пройденного пути от времени для трех тел. Какое из этих тел двигалось с большей скоростью?
S 
В) скорости одинаковые;
1 25. Модуль скорости тела за каждую секунду увеличивался в 2 раза. Какое утверждение будет правильным?
А) ускорение уменьшалось в 2 раза; Б) ускорение не изменялось;
В) ускорение увеличивалось в 2 раза
1.26. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на
землю. Чему равны путь l и перемещение S за все время его движения?
A) l = 10 м, S = 0 м; Б) l = 20 м, S = 0;
B) l = 10 м, S = 20 м; Г) l = 20 м, S = 10 м.
1.27. Тело, двигаясь равномерно по окружности, совершает 10 оборотов в секунду. Чему равен период вращения тела?
А) 



1.28. Автомобиль объехал Москву по кольцевой дороге, длина которой 109 км. Чему равны пройденный путь l и перемещение S автомобиля?
1.29. По графику зависимости скорости тела от времени определите вид движения.

А) равноускоренное; Б) равнозамедленное;
В) прямолинейное; Г) равномерное.
1.30. На графике изображена зависимость координаты х от времени. Чему равна начальная координата тела?
х 
Задания на 2 балла.
1.31. По графику зависимости скорости от времени определите ускорение тела в момент времени t = 2 с.
1.32. На рисунке представлены графики зависимости модуля скорости от времени движения трех тел. Какой из графиков соответствует равнозамедленному движению?

2 А)1; Б) 2; В)3; Г) все графики.
А) увеличится в 2 раза; Б) уменьшится в 2 раза;
В) не изменится; Г) увеличится в 4 раза.
1.34. На повороте трамвайный вагон движется с постоянной по модулю скоростью 5 м/с. Определите центростремительное ускорение трамвая, если радиус закругления пути равен 50 м.
А) 5 м; Б) 10 м; В) 50 м; Г) 100 м.
1.36. При равноускоренном движении в течение 5 с автомобиль увеличил скорость от 10 до
15 м/с. Чему равен модуль ускорения автомобиля?
1.38. Человек плывет вдоль берега по течению реки. Определите скорость пловца относительно берега по течению, если его скорость относительно воды 1,5 м/с, а скорость течения реки 0,5 м/с.
А) 0,5 м/с; Б) 1 м/с; В) 1,5 м/с; Г) 2 м/с.
1.41. Как изменяется скорость тела при его свободном падении за первую секунду?
А) увеличивается на 5 м/с; Б) увеличивается на 10 м/с;
В) увеличивается на 20 м/с.
1.42. Тело, брошенное горизонтально с башни высотой 6 м, упало на расстоянии 8 м от
основания башни. Чему равно перемещение тела?
А) 8 м; Б) 6 м; В) 14 м; Г) 10 м.
1.43. При движении тела сумма векторов всех сил, действующих на него, равна 0. Какой из приведенных на рисунках графиков зависимости модуля скорости тела от времени соответствует этому движению?
А
0 t (с) 0 t (с) 0 t (с) 0 t (с)
1.44. Скорость тела при прямолинейном равноускоренном движении увеличилась за 3
секунды в 3 раза и стала равной 9 м/с. Чему равно ускорение тела?
1.45. Тело, двигаясь прямолинейно и равноускоренно, увеличило свою скорость от 2 до 6
м/с за 4 секунды. Какой путь прошло тело за это время?
А) 10 м; Б) 12 м; В) 20 м; Г) 16 м.
А) 0; Б) 5 м/с; В) 7,5 м/с; Г) 15 м/с.
1.47. По графику зависимости модуля скорости от времени определите ускорение тела в
момент времени t = 2с.

А) 2 м/с 2 ;
1.48. Тело брошено вертикально вверх с начальной скоростью 10 м/с. Чему равен модуль его скорости через 0,5 с после броска?
1.49. Чему равна скорость тела при свободном падении через 4 с свободного падения, если начальная скорость равна 0? (g ≈ 10м/с 2 )
А) 20 м/с; Б) 40 м/с; В) 80 м/с; Г) 60 м/с.
1.50. Какой путь пройдет тело за первые 3 секунды свободного падения, если его начальная
скорость равна 0? (g ≈ 10 м/с 2 )
А) 18 м; Б) 30 м; В) 45 м; Г) 90 м.
1.51. Автомобиль на повороте движется по кривой траектории радиусом 50 м со скоростью 10 м/с. Каково ускорение автомобиля?
1.52. Тело движется по окружности радиусом 10 м. Период его обращения равен 20 секунд Чему равна скорость тела?
А) 2 м/с; Б) π м/с; В) 2π м/с; Г) 4π м/с.
1.53. На рисунке точками отмечены положения четырех движущихся слева направо тел через равные интервалы времени. На какой полосе зарегистрировано движение с возрастающей скоростью?

А) направлен по оси ОХ; Б) направлен против оси ОХ;
В) направлен перпендикулярно оси ОХ; Г) направление зависит от начальной координаты.
1.56. По графику определите ускорение и уравнение скорости движения тела.
v 
1.57. По графику определите ускорение и уравнение скорости движения тела.
1.58. По графику определите ускорение и уравнение скорости движения тела.

Задания на 3 балла
1.61. На графике приведена зависимость vx(t) для прямолинейного движения тела вдоль оси ОХ. Чему равна величина перемещения этого тела за 4 секунды?
1.62. Тело, брошенное вертикально вверх с начальной скоростью 20 м/с, двигаясь с постоянным ускорением, направленным вниз, достигло максимальной высоты h. Чему равна скорость тела на высоте 3/4h?
А) 5 м/с; Б) 10 м/с; В) 15 м/с; Г) 20 м/с.
1.63. По графику зависимости модуля скорости от времени, представленному на рисунке, определите перемещение тела за 3 секунды.

А) 48 м; Б) 12 м; В) 40 м; Г) 30 м.
1.66. Тело брошено вертикально вверх со скоростью v 0. Какой из графиков зависимости
проекции скорости от времени соответствует этому движению?

1.67. Какой путь тело пройдет за 5-ю секунду свободного падения с v 0 = 0? (g ≈ 10 м/с 2 )
А) 45 м; Б) 50 м; В)125 м; Г) 250 м.
1.68. Тело брошено вертикально вверх со скоростью 30 м/с. Чему равна максимальная высота подъема? (g ≈ 10 м/с 2 )
А) 135 м; Б) 45 м; В) 90 м; Г) 80 м.
1.69. Две материальные точки движутся по окружности радиусами R1 = R;
R 2 = 2R с одинаковыми скоростями. Сравните их центростремительные ускорения а1 и а2.
1.70. Тело движется по окружности радиусом 5 м. Частота вращения тела по окружности
0,1 Гц. Чему равна скорость тела?
А) 2 м/с; Б) 2π м/с; В) π м/с; Г) 4π м/с.
1.71. Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в
течение 4 секунд. С каким постоянным ускорением двигался автомобиль?
А) 5 с; Б) 6 с; В) 10 с; Г) 2 с.
1.73. Точки точильного круга, делающего один оборот за 0,5 с, движутся с постоянной по модулю скоростью. Чему равна скорость точек круга, которые удалены от его оси на 0,1 м?
А) ≈ 0,63 м/с; Б) 0,2 м/с; В) 1,26 м/с; Г) 12,6 м/с.
1.74. По уравнению координаты движения автомобиля х = 100 + 4t – 3 t 2 определите ускорение ах его движения.
1.75. На рисунке изображен график зависимости проекции скорости v x тела при
прямолинейном движении от времени t. Чему равна проекция перемещения Sх за 6 секунд?

1.76. На рисунке изображен график зависимости проекции скорости v х от времени t при
прямолинейном движении автомобиля. Определите проекцию ускорения ах и перемещения Sx за 2 секунды.
1.77. Плот равномерно плывет по реке со скоростью 3 км/ч. Сплавщик движется поперек
плота со скоростью 4 км/ч. Какова скорость сплавщика в системе отсчета, связанной с
берегом?
А) 3 км/ч; Б) 4 км/ч; В) 5 км/ч; Г) 7 км/ч.
1.78. Тело движется равномерно по окружности. Как изменится его центростремительное ускорение при увеличении скорости в 2 раза и уменьшении радиуса окружности в 4 раза?
А) увеличится в 2 раза; Б) увеличится в 8 раз;
В) увеличится в 16 раз; Г) уменьшится в 2 раза.
1.79. При равноускоренном прямолинейном движении скорость катера увеличивается за 10 секунд от 5 м/с до 9 м/с. Какой путь пройдет катер за это время?
А) 140 м; Б) 90 м; В) 50 м; Г) 70 м.
1.80. На рисунке представлен график зависимости модуля скорости четырех тел от времени. Какое из этих тел совершило наибольшее перемещение?

А) 1; Б) 2;
1.81. По графику скорости тела написать уравнение перемещения тела.

А ) S = 2t + t 2 ; Б ) S = 2t + 0,5t 2 ;
1.82. Камень, брошенный горизонтально из окна второго этажа здания с высоты 4 м, падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня?
А) 3 м; Б) 5 м; В) 7 м; Г) 10 м.
1.83. Величина скорости течения реки и скорости лодки относительно берега одинаковы и
образуют угол 60°. Под каким углом к направлению течения направлена скорость лодки
относительно воды?
А) 30°; Б) 60°; В) 90°; Г) 120°.
1.84. Плот плывет равномерно по реке со скоростью 6 км/ч. Человек движется поперек плота
со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?
А) 2 км/ч; Б) 7 км/ч; В) 10 км/ч; Г) 14 км/ч.
1.85. На графике изображена зависимость проекции скорости тела от времени, движущегося вдоль оси ОХ. Чему равен модуль перемещения тела к моменту времени t = 10 секунд.

1 2 3 4 5 6 7 8 9 10 t
1.86. По уравнению S = 2t + 0,5t 2 найдите среди предложенных график скорости.

0 1 2 3 t (с) 0 1 2 3 t (с) 0 1 2 3 t (с) 0 1 2 3 t (с)
А) 1м/с; Б) 3 м/с; В) 5 м/с; Г) 7 м/с.
1.88. Поезд длиной 200 м въезжает в тоннель длиной 300 м, двигаясь равномерно со
скоростью v = 10 м/с. Через какое время поезд полностью выйдет из тоннеля?
А) 10 с; Б) 20 с; В) 30 с; Г) 50 с.
1.89. Две моторные лодки движутся навстречу друг другу. Скорости лодок относительно
воды равны 3 и 4 м/с. Скорость течения реки равна 2 м/с. Через какое время после их встречи
расстояние между лодками станет равным 84 м?
А) 12 с; Б) 21 с; В) 28 с; Г) 42 с.
А)